Система, как отношение на абстрактных множествах

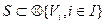Одним из центральных понятий теории систем является поня­тие системы, определенное в теоретико-множественных терминах:

где V, — вес компоненты; iÎI — декартова произведения ÄV_i , называемые объектами системы S; I — множество индексов. В кибернетике наибольший интерес представляют системы с дву­мя объектами — входным объектом X и выходным объектом Y:

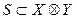Основными причинами определения системы как теоретико-множественного отношения являются следующие:

1. Система определяется в терминах ее наблюдаемых свойств или, точнее говоря, в терминах взаимосвязей между этими свой­ствами, а не тем, что они на самом деле собой представляют (т. е. не с помощью физических, химических, биологических, социа­льных или других явлений). Это вполне согласуется с природой системных исследований, направленных на выяснение организации и взаимосвязи элементов системы, а не на изучение конкретных механизмов в системе.

2. Определение системы как отношения вида (3.1) является предельно общим. Конечно, различным системам отвечают и различные способы задания описания (дифференциальные уравнения, булева алгебра, графы и т. д.), но все они есть не более чем отношения вида (3.1). В условиях предельно нечеткой инфор­мации, когда систему удается описать лишь качественно, все словесные утверждения в силу их лингвистических функций определяют отношения типа (3.1). Действительно, каждое высказывание содержит две основные лингвистические категории: термы (денотаты) и функторы. Напомним, что термы используются для обозначения объектов, а функторы — для обозначения отношения между ними. И для каждого правильного множества словесных утверждений существует отношение (в математическом смысле слова), описывающее формальную взаимосвязь между объектами. Таким образом, система всегда является отношением в смысле (3.1), а уже более узкие классы систем определяются более точно своими специфическими средствами.

3. Системы часто задаются с помощью некоторых уравнений относительно соответствующих переменных. Каждой такой переменной можно поставить в соответствие некоторый объект системы, описывающей область значений соответствующей переменной. Утверждая, что система описывается системой уравнений относительно некоторого множества переменных, в сущности считают, что система есть отношение над соответствующими объектами, порожденными этими переменными (по одному объекту на каждую переменную, область значений которой он представляет). При этом любая комбинация элементов этих объектов, принадлежащая этому отношению, удовлетворяет исходной системе уравнений.

Под отношением понимается подмножество конечной декар­товой степени Аⁿ = А ´ А ´ ... ´A данного множества А, т. е. подмножество систем (a₁, a₂, ..., a_n) из n элементов множества А.

Подмножество RМ.Аⁿ называется n-местным или n-арным отношением в множестве А. Число n называется рангом или типом отношения R. Множество всех n-арных отношений в множестве А относительно операций И и З является булевой алгеброй.

Для построения теории систем на теоретико-множественном уровне, исходя из определения (3.1), необходимо наделить систему как отношение некоторой дополнительной структурой. Это можно сделать двумя способами:

ввести дополнительную структуру для элементов объектов системы; например, рассматривать сам элемент v_i,О V_i как некоторое множество с подходящей структурой;

ввести структуру непосредственно для самих объектов системы V_i, iОI.

Первый способ приводит к понятию (абстрактных) временных систем, а второй — к понятию алгебраических систем.