Свойства определенных интегралов
1. Постоянный множитель можно выносить за знак интеграла
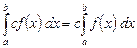 . (3)
. (3)
2. Определенный интеграл от алгебраической суммы равен алгебраической сумме определенных интегралов:
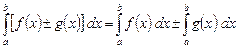 . (4)
. (4)
Пример. Вычислить 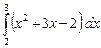 .
.
На основании свойств 1 и 2 получаем
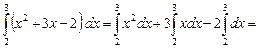
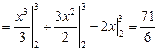
3. Определенный интеграл меняет знак при перестановке пределов интегрирования
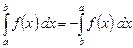 . (5)
. (5)
Это следует из того, что
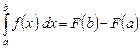 , а
, а 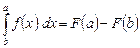 .
.
4. Теорема о среднем. Между точками a и b имеется такая точка c, что
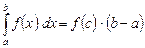 . (6)
. (6)
Доказательство. По формуле Ньютона-Лейбница 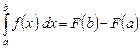 . Применим к первообразной
. Применим к первообразной 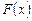 формулу Лагранжа:
формулу Лагранжа: 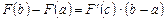 . Но
. Но 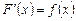 , следовательно
, следовательно 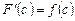 . Итак,
. Итак,
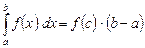 .
.
5. Если 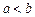 и
и 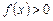 , то
, то
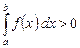 . (7)
. (7)
Действительно, в этом случае 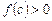 и
и 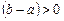 , и из формулы (6) получаем
, и из формулы (6) получаем
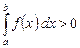 .
.
6. Если 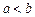 и
и 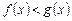 , то
, то
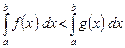 . (8)
. (8)
Действительно,
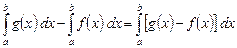 .
.
По условию 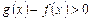 и по свойству 5:
и по свойству 5:
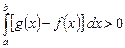 .
.
Следовательно,
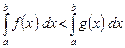 .
.
7. Если 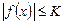 , то
, то
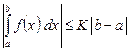 . (9)
. (9)
Это следует из того, что 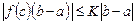 .
.
Приложения определенного интеграла
Рассмотрим приложения интеграла к вычислению площадей, объемов, механической работы.
Вычисление площадей
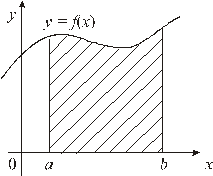
Пусть 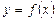 – непрерывная на
– непрерывная на 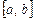 функция,
функция, 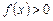 . Рассмотрим фигуру, ограниченную сверху графиком функции
. Рассмотрим фигуру, ограниченную сверху графиком функции 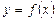 , снизу – отрезком
, снизу – отрезком 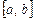 оси Ox, с боков – прямыми
оси Ox, с боков – прямыми 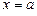 ,
, 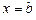 .
.
 |
| Рис. 1 |
Эту фигуру называют криволинейной трапецией. Площадь S этой фигуры вычисляется по формуле
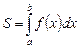 . (1)
. (1)
Приведем обоснование этой формулы. Для того чтобы определить площадь криволинейной трапеции ABCD (см. рис. 2), изучим поведение площади переменной фигуры ABMN, заключенной между начальной ординатой 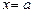 и ординатой, соответствующей произвольно выбранному на
и ординатой, соответствующей произвольно выбранному на 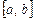 значению x. Площадь этой криволинейной трапеции ABMN есть функция, зависящая от x; обозначим ее через
значению x. Площадь этой криволинейной трапеции ABMN есть функция, зависящая от x; обозначим ее через 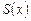 .
.
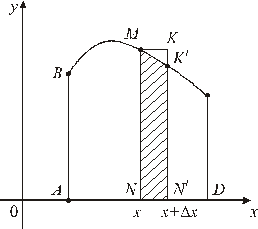 |
| Рис. 2 |
Вычислим производную этой функции 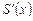 . Для этого придадим x приращение Dx. Тогда площадь
. Для этого придадим x приращение Dx. Тогда площадь 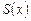 получит приращение DS, равное площади фигуры
получит приращение DS, равное площади фигуры 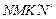 . Если приращение Dx мало, то DS приблизительно равно площади прямоугольника
. Если приращение Dx мало, то DS приблизительно равно площади прямоугольника 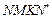 , равной
, равной 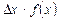 . Рассмотрим отношение
. Рассмотрим отношение 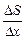 . Оно приблизительно равно
. Оно приблизительно равно 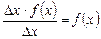 . Если
. Если 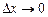 , то приближенное равенство перейдет в точное
, то приближенное равенство перейдет в точное
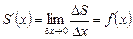 .
.
Итак, переменная площадь 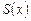 есть первообразная для
есть первообразная для 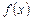 . Следовательно, если
. Следовательно, если 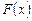 – какая-нибудь первообразная для
– какая-нибудь первообразная для 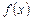 , то
, то
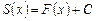 .
.
Положим 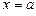 . Очевидно,
. Очевидно, 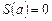 . Следовательно,
. Следовательно,
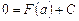 .
.
Поэтому
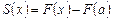 .
.
При 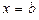 получаем
получаем
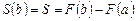 .
.
Но это означает, что
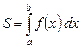 .
.
Пример 1. Найти площадь фигуры (криволинейной трапеции), ограниченной параболой 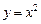 , прямыми
, прямыми 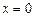 ,
, 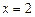 и осью Ox.
и осью Ox.
Решение.
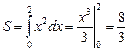 .
.
Пример 2. Найти площадь фигуры, ограниченной линиями 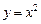 ,
, 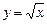 .
.
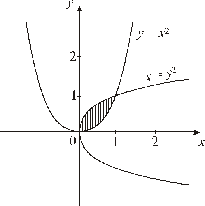 | Решение. Очевидно, эти линии пересекаются в точках с абсциссами 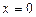 и и 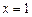 . Искомая площадь есть разность площадей криволинейных трапеций, ограниченных сверху соответственно линиями . Искомая площадь есть разность площадей криволинейных трапеций, ограниченных сверху соответственно линиями 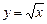 и и 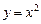 : : |
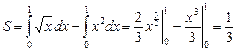 .
.
В примере 2 рассмотрен частный случай вычисления площади фигуры, ограниченной одной кривой сверху, другой кривой – снизу.
Вообще, если фигура ограничена сверху кривой 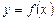 , снизу – кривой
, снизу – кривой 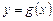 , а с боков – соответственно прямыми
, а с боков – соответственно прямыми 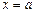 ,
, 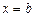 , то ее площадь выражается формулой:
, то ее площадь выражается формулой:
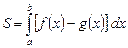 . (2)
. (2)
