Лекция 2. Предел. Непрерывность функции
Здесь мы будем рассматривать упорядоченные переменные величины. Переменная x есть упорядоченная переменная, если известна ее область изменения и для любых двух ее значений известно, какое из них есть предыдущее и какое – последующее.
Определение 1.Число a называется пределом переменной величины x, если для любого (произвольно малого) числа  существует такое значение переменной x, что для всех последующих значений выполняется неравенство
существует такое значение переменной x, что для всех последующих значений выполняется неравенство
 .
.
Если a есть предел переменной x, то говорят, что x стремится к пределу a, и пишут
 , или
, или  .
.
Пример 1. Переменная величина x принимает следующие значения:
 ,
,  ,
,  , ...,
, ...,  , ...
, ...
Легко убедиться, что эта переменная величина стремится к единице. Действительно,
 .
.
Пусть задано  . Тогда для всех номеров n, удовлетворяющих условию
. Тогда для всех номеров n, удовлетворяющих условию  , будет выполняться неравенство
, будет выполняться неравенство  , т.е.
, т.е.
 .
.
В рассмотренном примере переменная величина стремится к пределу, убывая.
Пример 2. Переменная величина x последовательно принимает значения
 ,
,  ,
,  , ...,
, ...,  , ...
, ...
Эта переменная имеет предел, равный 2. При этом переменная стремится к своему пределу, возрастая.
Пример 3.  ,
,  ,
,  ,
,  , ...,
, ...,  , ...
, ...
Эта переменная стремится к единице, «колеблясь» вокруг своего предела, т.е. принимая значения то больше, то меньше своего предела.
Замечание 1. Постоянную величину c можно рассматривать как переменную, все значения которой одинаковы.
Замечание 2. Не всякая переменная величина имеет предел.
Замечание 3. Можно доказать, что переменная величина не может иметь двух разных пределов.
Определение 2. Переменная x стремится к бесконечности, если для любого  существует такое значение x, начиная с которого все последующие значения переменной удовлетворяют неравенству
существует такое значение x, начиная с которого все последующие значения переменной удовлетворяют неравенству
 . (1)
. (1)
В этом случае пишем  .
.
Если в нашем определении неравенство (1) эквивалентно неравенству  , то говорим, что x «стремится к плюс бесконечности», и пишем
, то говорим, что x «стремится к плюс бесконечности», и пишем  ; если же неравенство (1) эквивалентно неравенству
; если же неравенство (1) эквивалентно неравенству  , то говорим, что x «стремится к минус бесконечности», и пишем
, то говорим, что x «стремится к минус бесконечности», и пишем  .
.
Предел функции
Функция 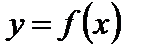 представляет собой переменную величину, и поэтому к ней применимо понятия предела, следует лишь указать предел, к которому стремится ее аргумент.
представляет собой переменную величину, и поэтому к ней применимо понятия предела, следует лишь указать предел, к которому стремится ее аргумент.
Сформулируем строгое определение предела функции. Пусть функция 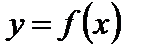 определена в некоторой окрестности точки a, кроме, может быть, точки a.
определена в некоторой окрестности точки a, кроме, может быть, точки a.
Определение 1. Число b называется пределом функции 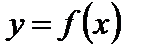 при x, стремящемся к a, если для любого (сколь угодно малого) числа
при x, стремящемся к a, если для любого (сколь угодно малого) числа 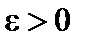 существует такое
существует такое 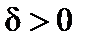 , что для всех x, отличных от a и удовлетворяющих неравенству
, что для всех x, отличных от a и удовлетворяющих неравенству
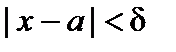 ,
,
выполняется неравенство
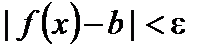 .
.
Если b есть предел 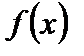 при
при 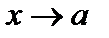 , то пишут
, то пишут
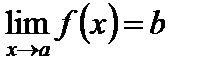 ,
,
или 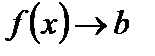 при
при 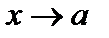 .
.
Дадим геометрическую иллюстрацию определения предела:
для всех точек 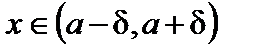 точки графика функции
точки графика функции 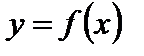 лежат внутри полосы, ограниченной прямыми
лежат внутри полосы, ограниченной прямыми 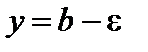 и
и 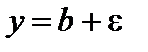 (рис. 11).
(рис. 11).
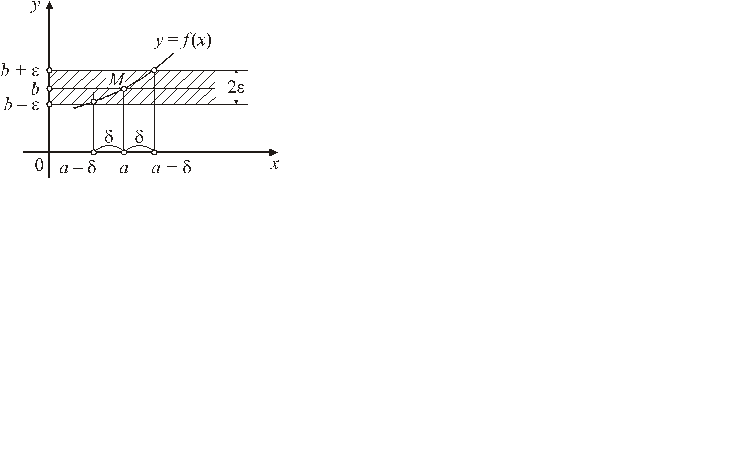 |
| Рис. 11 |
Замечание. Если 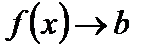 при
при 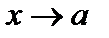 и при этом
и при этом  , то говорим, что
, то говорим, что 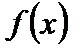 стремится к b слева, и пишем
стремится к b слева, и пишем 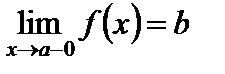 . Аналогично определяется предел справа:
. Аналогично определяется предел справа: 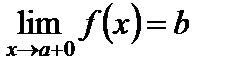 , если
, если 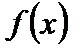 стремится к b, когда x стремится к a, оставаясь больше a. В частности, если
стремится к b, когда x стремится к a, оставаясь больше a. В частности, если 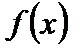 стремится к b при
стремится к b при 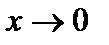 справа (соответственно слева), то пишем
справа (соответственно слева), то пишем 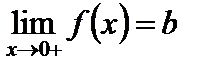 (соответственно
(соответственно 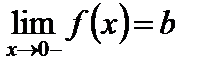 ).
).
Данное выше определение предела относилось к случаю, когда x стремится к конечному пределу а. Рассмотрим теперь случай 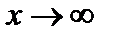 .
.
Определение 2. Число b есть предел функции 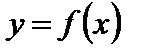 при
при 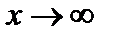 , если для любого (сколь угодно малого) числа
, если для любого (сколь угодно малого) числа 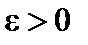 существует такое
существует такое 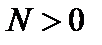 , что для всех x, удовлетворяющих неравенству
, что для всех x, удовлетворяющих неравенству 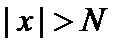 , выполняется неравенство
, выполняется неравенство
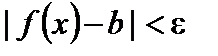 .
.
В этом случае пишем 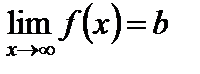 .
.
Если переменная величина является последовательностью, т.е. все ее значения можно занумеровать натуральными числами
 ,
, 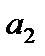 , ...,
, ..., 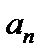 , ...,
, ...,
то ее можно рассматривать как функцию натурального аргумента:
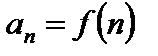 ,
, 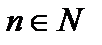 .
.
Определение 2 можно рассматривать, в частности, и как определение предела последовательности (если считать, что аргумент x принимает лишь целые положительные значения).
2.2. Бесконечно малые величины. Связь переменной
величины с ее пределом. Свойства бесконечно малых
Определение.Переменная величина называется бесконечно малой, если она стремится к нулю.
В частности, функция 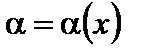 есть бесконечно малая при
есть бесконечно малая при 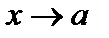 (или при
(или при 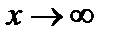 ), если
), если 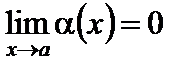 (соответственно,
(соответственно, 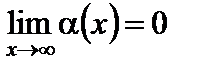 ).
).
Теорема. Число b есть предел переменной y тогда и только тогда, когда
(1) 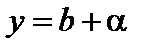 ,
,
где a – бесконечно малая.
Доказательство. 1. Необходимость. Пусть 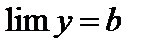 . Пусть задано
. Пусть задано 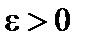 . Тогда для всех значений y, начиная с некоторого, будет
. Тогда для всех значений y, начиная с некоторого, будет 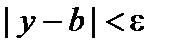 . Обозначим
. Обозначим 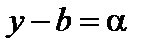 . Очевидно, для всех значений a, начиная с некоторого, будет
. Очевидно, для всех значений a, начиная с некоторого, будет 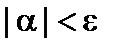 , следовательно, a – бесконечно малая. Итак,
, следовательно, a – бесконечно малая. Итак,
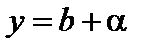 ,
,
где a – бесконечно малая.
2. Достаточность. Из равенства (1) следует 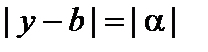 . Пусть задано
. Пусть задано 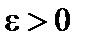 . Так как a – бесконечно малая, то для всех значений a, начиная с некоторого, будет
. Так как a – бесконечно малая, то для всех значений a, начиная с некоторого, будет 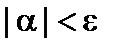 , следовательно, для всех значений y, начиная с некоторого, будет
, следовательно, для всех значений y, начиная с некоторого, будет 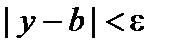 . А это значит, что
. А это значит, что 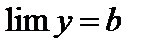 .
.
Теорема доказана.
Перечислим свойства бесконечно малых величин.
1. Если a – бесконечно малая и не обращается в нуль, то 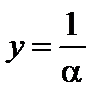 стремится к бесконечности.
стремится к бесконечности.
Заметим, что переменная величина, стремящаяся к бесконечности, называется бесконечно большой. Поэтому сформулированное выше свойство можно переформулировать так: величина, обратная бесконечно малой, есть бесконечно большая величина.
2. Алгебраическая сумма двух (трех и вообще конечного числа) бесконечно малых величин есть бесконечно малая.
Иначе говоря, если 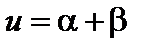 , где a, b – бесконечно малые, то и u – бесконечно малая.
, где a, b – бесконечно малые, то и u – бесконечно малая.
3. Произведение бесконечно малой величины на величину ограниченную есть величина бесконечно малая.
(Т. е. если a – бесконечно малая, z – ограниченная, то 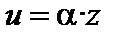 есть бесконечно малая.)
есть бесконечно малая.)
Следствие 1.Произведение двух бесконечно малых есть величина бесконечно малая.
Следствие 2. Если a – бесконечно малая, 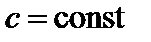 , то
, то 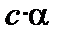 – бесконечно малая.
– бесконечно малая.
4. Если a– бесконечно малая, а переменная величина z имеет предел, отличный от нуля, то 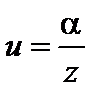 есть величина бесконечно малая.
есть величина бесконечно малая.
Следует заметить, что сформулированные свойства 1–4 являются, по существу, теоремами и в более подробном курсе математики излагаются с доказательствами. Здесь мы докажем одно из них, например свойство 3.
Пусть a– бесконечно малая, z – ограниченная величина, 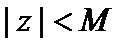 . Надо доказать, что
. Надо доказать, что 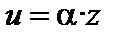 – бесконечно малая. Пусть задано
– бесконечно малая. Пусть задано 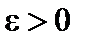 . Возьмем
. Возьмем 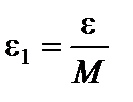 . Так как a– бесконечно малая, то для всех значений a, начиная с некоторого, будет
. Так как a– бесконечно малая, то для всех значений a, начиная с некоторого, будет 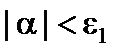 , т.е.
, т.е. 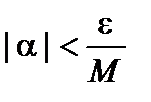 . Тогда
. Тогда 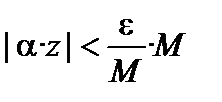 , т.е.
, т.е. 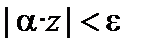 . Доказательство закончено.
. Доказательство закончено.
2.3. Предел суммы, произведения, частного.
Предельный переход в неравенствах
Мы будем рассматривать предел функций 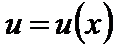 ,
, 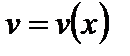 при
при 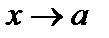 или при
или при 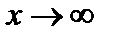 .
.
1. Предел алгебраической суммы конечного числа переменных равен алгебраической сумме пределов:
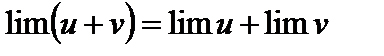 .
.
(Вообще 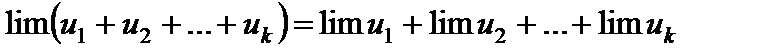 .)
.)
2. Предел произведения конечного числа переменных равен произведению пределов этих переменных:
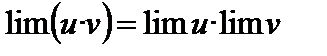 .
.
(Вообще 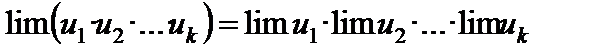 .)
.)
Следствие. Постоянный множитель можно выносить за знак предела: 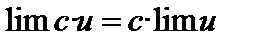 .
.
3. Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля:
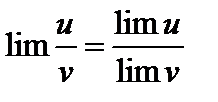 (если
(если 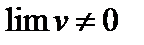 ).
).
Утверждения 1–3 также являются теоремами. Их доказательства основаны на теореме о связи переменной величины с ее пределом.
Приведем в качестве примера доказательство утверждения 2.
Пусть 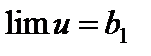 ,
, 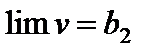 . Надо доказать, что
. Надо доказать, что 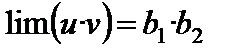 . Имеем:
. Имеем: 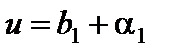 ,
, 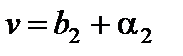 , где
, где 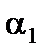 ,
, 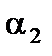 – бесконечно малые.
– бесконечно малые.
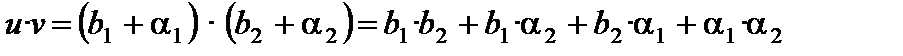 .
.
Обозначим 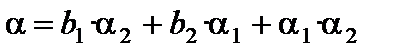 . В соответствии со свойствами бесконечно малых a есть бесконечно малая. Так как
. В соответствии со свойствами бесконечно малых a есть бесконечно малая. Так как 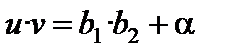 , где a – бесконечно малая, то
, где a – бесконечно малая, то 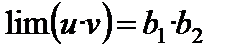 . Доказательство закончено.
. Доказательство закончено.
Можно доказать также следующие утверждения.
4. Если переменная y неотрицательна, то ее предел неотрицателен: если 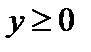 , то
, то 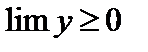 .
.
5. Если для переменных u и v выполняется неравенство 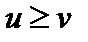 , то
, то 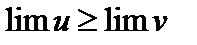 .
.
6. Если для переменных u, z и v выполняются неравенства 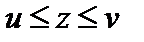 и при этом u и v стремятся к одному пределу b (
и при этом u и v стремятся к одному пределу b ( 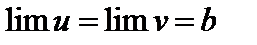 ), то переменная z стремится к тому же пределу:
), то переменная z стремится к тому же пределу: 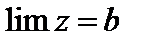 .
.
7. Достаточный признак существования предела:если переменная величина v возрастает и ограничена, т.е. 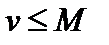 , то эта переменная величина имеет предел:
, то эта переменная величина имеет предел:
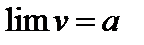 , где
, где 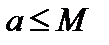 .
.
Аналогичное утверждение справедливо и для убывающей ограниченной величины.
Замечательные пределы
1. Предел функции 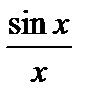 при
при 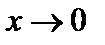 равен 1:
равен 1:
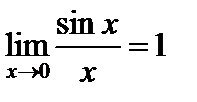 . (1)
. (1)
Рассмотрим примеры применения формулы (1).
Пример 1.
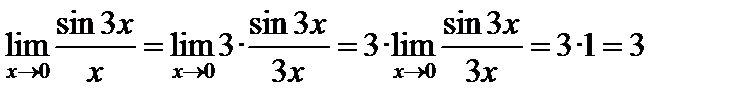 .
.
Пример 2.
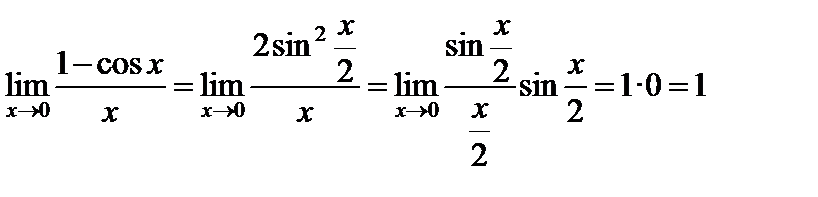 .
.
2. Предел переменной величины 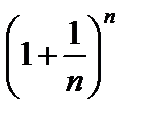 при
при 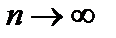 .
.
Теорема. Переменная величина 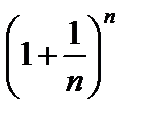 при
при 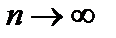 имеет предел, заключенный между 2 и 3.
имеет предел, заключенный между 2 и 3.
Доказательство этой теоремы основано на достаточном признаке существования предела, сформулированном выше.
Определение.Предел переменной величины 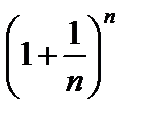 при
при 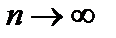 называется числом е:
называется числом е:
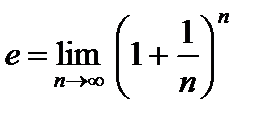 .
.
Заметим, что число e – иррациональное число
е = 2,7182818284...
(Обычно в вычислениях полагают 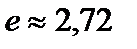 .)
.)
Можно доказать, что
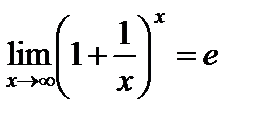 . (3)
. (3)
(В формуле (2) переменная 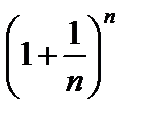 является последовательностью, в формуле (3) переменная
является последовательностью, в формуле (3) переменная 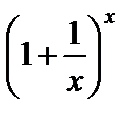 является функцией.)
является функцией.)
Сделав в формуле (3) замену 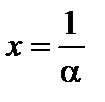 , получаем
, получаем
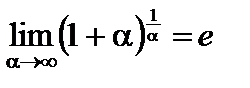 . (4)
. (4)
Примеры:
1) 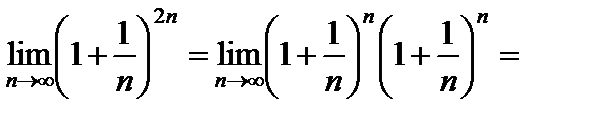
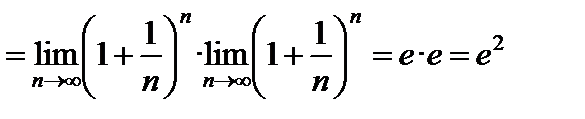 ;
;
2) 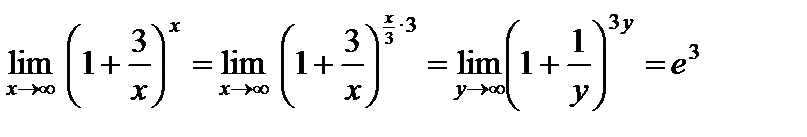 ;
;
3) 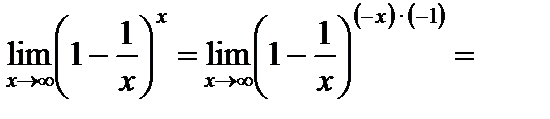
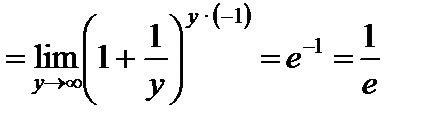 ;
;
4) 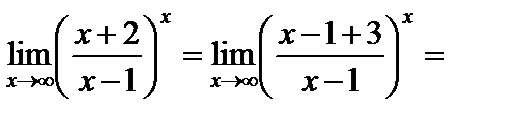
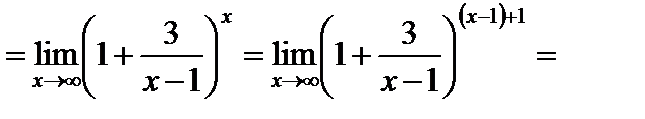
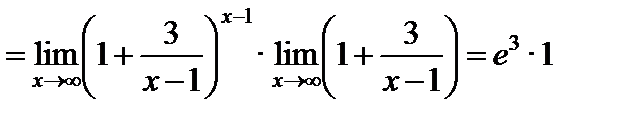 .
.
Число е играет очень важную роль в математике и ее приложениях.
Показательная функция с основанием е:
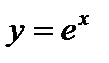
называется экспонентной.
Логарифмы с основанием е называют натуральными логарифмами и обозначают 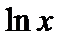 , т.е. вместо
, т.е. вместо 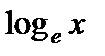 пишут
пишут 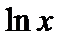 . Очевидно, если
. Очевидно, если 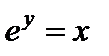 , то
, то 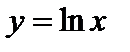 .
.
Непрерывность функций
Определение 1. Функция 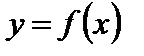 называется непрерывной в точке
называется непрерывной в точке 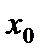 , если она определена в этой точке и в некоторой окрестности этой точки и если
, если она определена в этой точке и в некоторой окрестности этой точки и если
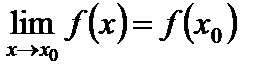 .
.
С геометрической точки зрения непрерывная функция – это функция, график которой есть непрерывная кривая. Существует несколько эквивалентных определений непрерывности.
Обозначим разность 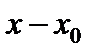 через
через 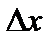 . Будем говорить, что при переходе от значения
. Будем говорить, что при переходе от значения 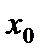 к значению x аргумент получает приращение
к значению x аргумент получает приращение 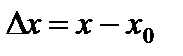 *. При этом функция y получает соответствующее приращение
*. При этом функция y получает соответствующее приращение 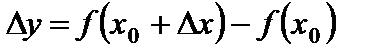 . С учетом сказанного, равенство (1) принимает вид:
. С учетом сказанного, равенство (1) принимает вид:
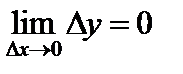 .
.
Определение. Функция 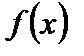 называется непрерывной в точке
называется непрерывной в точке 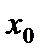 , если она определена в этой точке и некоторой ее окрестности и если
, если она определена в этой точке и некоторой ее окрестности и если
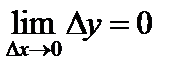 . (2)
. (2)
(Это определение легко запоминается в следующей форме: «функция непрерывна, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции».)
Пример. Покажем, что функция 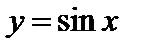 непрерывна в произвольной точке
непрерывна в произвольной точке 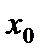 . Действительно, придадим аргументу приращение
. Действительно, придадим аргументу приращение 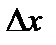 . Тогда функция получит приращение
. Тогда функция получит приращение
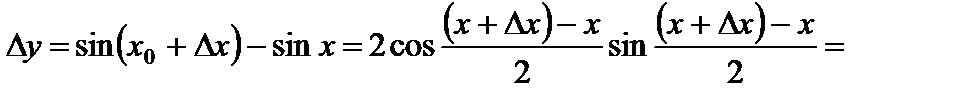
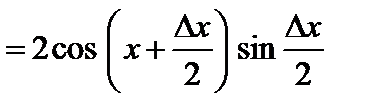 .
.
Если 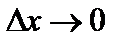 , то
, то 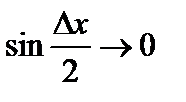 (так как
(так как 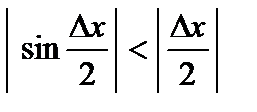 ); при этом
); при этом 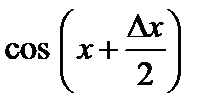 – ограничена. Поэтому
– ограничена. Поэтому
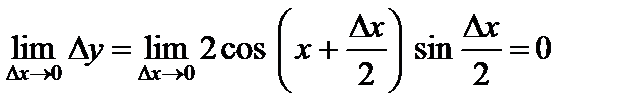 .
.
Следовательно, функция 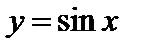 непрерывна.
непрерывна.
Аналогично можно доказать, что любая основная элементарная функция непрерывна в каждой точке, в которой она определена.
Справедливы следующие теоремы:
1. Если функции 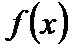 и
и 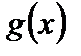 непрерывны в точке
непрерывны в точке 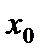 , то их сумма
, то их сумма 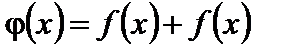 также непрерывна в этой точке.
также непрерывна в этой точке.
2. Произведение двух непрерывных функций есть непрерывная функция.
3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль (т.е. если 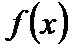 и
и 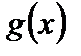 непрерывны в точке
непрерывны в точке 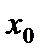 и
и 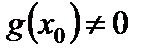 , то
, то 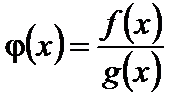 непрерывна в точке
непрерывна в точке 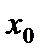 ).
).
4. Если 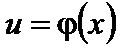 непрерывна при
непрерывна при 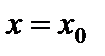 и
и 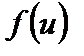 непрерывна в точке
непрерывна в точке 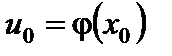 , то сложная функция
, то сложная функция 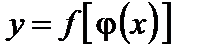 непрерывна в точке
непрерывна в точке 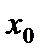 .
.
Доказательства этих утверждений основаны на свойствах пределов.
На этих утверждениях* основана следующая теорема.
Теорема. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Если функция 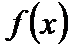 не является непрерывной в точке
не является непрерывной в точке 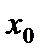 , то точка
, то точка 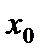 называется точкой разрыва функции
называется точкой разрыва функции 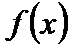 . Различают точки разрыва первого рода, когда существуют конечные пределы
. Различают точки разрыва первого рода, когда существуют конечные пределы 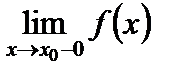 и
и 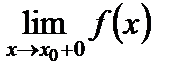 , но
, но 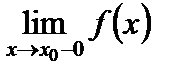 ¹
¹ 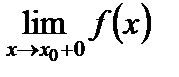 , и второго рода, когда хотя бы один из пределов слева и справа бесконечен или не существует. Среди точек разрыва первого рода следует отметить также точки устранимого разрыва, когда предел функции
, и второго рода, когда хотя бы один из пределов слева и справа бесконечен или не существует. Среди точек разрыва первого рода следует отметить также точки устранимого разрыва, когда предел функции 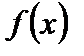 при
при 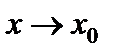 существует, но не равен
существует, но не равен 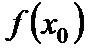 .
.
Примеры:
1) 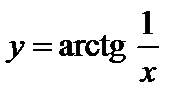 . Здесь
. Здесь 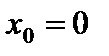 – точка разрыва первого рода, так как предел при
– точка разрыва первого рода, так как предел при 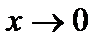 слева равен
слева равен 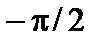 , а предел при
, а предел при 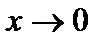 справа равен
справа равен 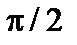 ;
;
2) 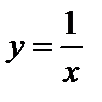 . Здесь
. Здесь 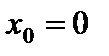 – точка разрыва второго рода;
– точка разрыва второго рода;
3) 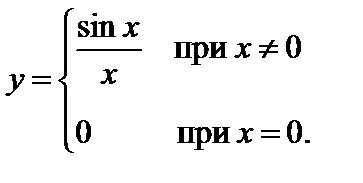 Здесь
Здесь 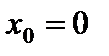 – точка устранимого разрыва, так как существует
– точка устранимого разрыва, так как существует 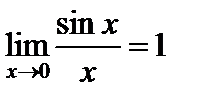 .
.
Определение 3.Если функция 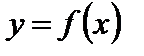 непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.
непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.
