Действия с матрицами на компьютере в EXCEL

Рассмотрим применение табличного процессора EXCEL для работы с матрицами.

Процессор EXCEL работает с числовыми матрицами и может осуществлять следующие операции:

1. сложение (вычитание) матриц, умножение матриц на число,

2. преобразования матрицы с целью получения нулей,

3. вычисление определителя матрицы,

4. транспонирование матрицы,

5. нахождение обратной матрицы.

Сложение матриц, умножение матрицы на число, преобразование матрицы осуществляются с помощью строки формул. Для нахождения определителя матрицы, транспонированной матрицы, обратной матрицы, а также для умножения матриц следует пользоваться соответствующими встроенными функциями: МОПРЕД; ТРАНСП; МОБР; МУМНОЖ. К сожалению, нет встроенной функции для определения ранга матрицы. Ранг придется находить переходом к эквивалентной матрице. Такой же переход полезен и для исследования линейных систем.

Сложение матриц.

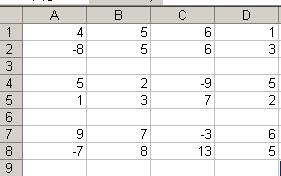
Рис.3

В ячейки 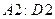введена матрица .

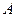В ячейки 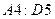введена матрица .

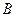В ячейку 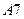введена формула 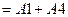и скопирована в диапазон .

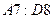Умножение матрицы на число.

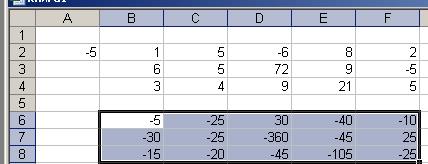
Рис.4

В ячейки 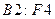введена матрица ,

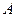В ячейку 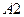введено число .

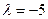В ячейку 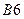введена формула 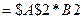и скопирована в диапазон .

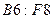Вычисление определителя, транспонирование, нахождение обратной матрицы.

Перечисленные операции проводятся с помощью соответствующих встроенных функций. При выполнении операций транспонирования, умножения матриц, нахождения обратной матрицы необходимо предварительно выделить диапазон ячеек для записи результата. Результат получается нажатием клавиш 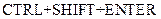(ввод массива).

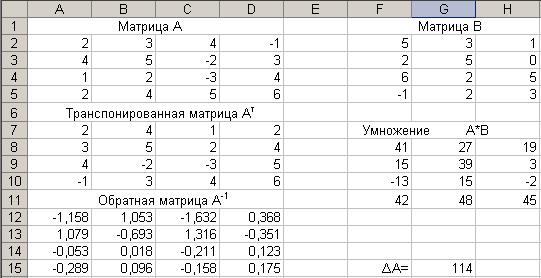
Рис.5

В ячейки 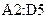введена матрица 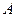, в ячейки 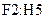- матрица .

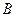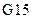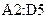В ячейку введем формулу =МОПРЕД, заполним поле значений аргумента , получаем значение определителя матрицы .

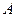Пример 14. Вычислить обратную матрицу для .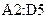

Выделим диапазон ячеек 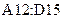для записи обратной матрицы. Теперь надо вызвать Мастер функций, выбрать имя функции МОБР, ввести в поле значений аргумента функции 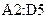и нажать клавиши 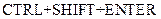(ввод массива).

Пример 15. Умножить матрицы 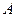и .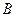

Определим размерность матрицы 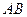(результата умножения): 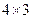, и выделим диапазон 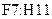для записи этой матрицы.

Для умножения надо вызвать Мастер функций, выбрать имя функции МУМНОЖ, ввести в поле значений 1 аргумента функции первую матрицу, в поле 2 – вторую матрицу, и нажать клавиши 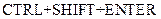(ввод массива). В ячейках 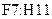− результат умножения .

Вычисление ранга матрицы.

Будем последовательно получать нули в первом, втором и т.д. столбцах ниже диагональных элементов.

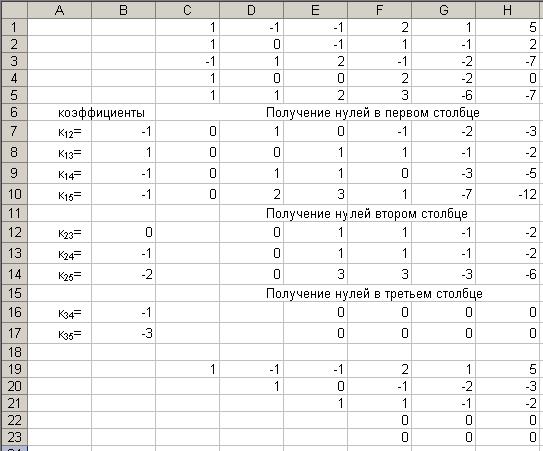
Рис.6

В ячейки 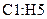введем матрицу (пример 10).

Получим нули в первом столбце матрицы 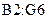. Для этого в ячейку 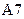введем формулу 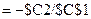и скопируем ее в ячейки 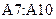, в ячейку 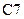введем формулу 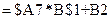и скопируем ее в ячейки .

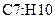Аналогично получаем нули во втором столбце. В ячейку 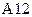введем формулу 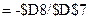и скопируем ее в ячейку 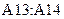. В ячейку 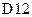введем формулу 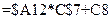и скопируем ее в ячейки .

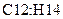Дальше получаем нули в третьем столбце. В ячейку 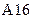введем формулу 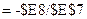и скопируем ее в ячейку 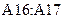. В ячейку 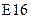введем формулу 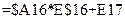и скопируем ее в ячейки .

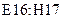Получили полностью нулевые строки. Ниже копированием значений (специальная вставка) записана преобразованная матрица (нули ниже диагонали опущены). Следовательно, ранг матрицы равен трем.