Использование пакета mathcad
ИСПОЛЬЗОВАНИЕ ПАКЕТА MATHCAD
ДЛЯ МАТЕМАТИЧЕСКИХ И ИНЖЕНЕРНЫХ РАСЧЕТОВ
С ПРАКТИЧЕСКИМИ ЗАДАНИЯМИ
УЧЕБНОЕ ПОСОБИЕ
Самара, 2015
УДДК - 004.772
ББК 3.32.97
Авторы: к.т.н., доцент кафедры ИВТ Коваленко Т.А, доцент кафедры ИВТ Сирант О.В.
Учебное пособие по дисциплине «Информатика» «Использование пакета MathCAD для математических и инженерных расчетов с практическими заданиями». Для направлений: 27.03.04 – Управление в технических системах; 09.03.04 – Программная инженерия; 11.03.02 – Инфокоммуникационные технологии и системы связи; 09.03.01 – Информатика и вычислительная техника; 09.03.02 – Информационные системы и технологии; 02.03.03 – Математическое обеспечение и администрирование информационных систем.
ISBN
Учебное пособие предназначено для студентов первого курса дневной и заочной формы обучения. В нем рассмотрены методы решения задач с помощью пакета программ MathCAD в рамках учебной дисциплины «Информатика».
Пособие представлено в двух частях теоретической и практической. В теоретическое части дается представление о пакете MathCAD его возможностях, которые позволяют решать сложные инженерные задачи. Вторая часть состоит из 6 лабораторных работ. Все задачи классифицированы, т.е. объединены в некоторые группы.
Пособие позволяет рассмотреть не только теоретические вопросы, но и выполнить самостоятельно лабораторные работы.
Использование данного учебного пособия является хорошим подспорьем для студентов технических специальностей.
Данное пособие поможет студентам использовать математические методы в технических приложениях (ОК-9, ПК-2), повысить знания принципов алгоритмизации и программирования (ОК-9, ПК-1) и овладеть основными методами работы на компьютере с использованием универсальных прикладных программ (ОК-9, ПК-2).
Материал, представленный в учебном пособии, является актуальным. Он изложен доступным для студентов языком.
Учебное пособие является необходимым и полезным в учебном процессе.
Рецензенты: к.т.н., доцент СГАУ Баяндина Т. А.
д.т.н., профессор ПГУТИ Тарасов В.Н.
ОГЛАВЛЕНИЕ
Введение. 4
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.. 6
Основные сведения о пакете Mathcad. 6
Mathcad-документ и его структура. 7
Простейшие конструкции системы Mathcad. 8
Функции, определяемые пользователем.. 8
Переменные диапазона (ранжированные переменные) 9
Текстовые фрагменты.. 9
Графические области. 10
Организация условий в Mathcad. 10
Матрицы и матричные операторы Mathcad. 11
Решение уравнений средствами Mathcad. 12
ПРАКТИЧЕСКАЯ ЧАСТЬ.. 24
Лабораторная работа №1 Табулирование функций и нахождение корней уравнений в системе Mathcad 25
Лабораторная работа №2 Функции условных выражений. 29
Лабораторная работа №3 Функции для обработки векторов и матриц. 32
Лабораторная работа №4 Решение систем линейных и нелинейных уравнений 34
Лабораторная работа №5 Решение уравнений с помощью программного модуля 39
Лабораторная работа №6 Построение графиков поверхности. 44
Список использованных источников. 52
Введение
Данное пособие рассчитано для использования студентами 1 курса на лабораторно–практических занятиях по предмету «Информатика».
Инженерные и научные задачи часто приводят к решению различных уравнений или систем уравнений, описывающих поведение параметров объекта, например расчеты нагрузки в сети или тепловые потоки через стены дома, оптимизация построения сетей. Совокупность всех уравнений и дополнительных условий, которым должно удовлетворять решение, называется математической моделью. Простая математическая модель – это совокупность алгебраических формул, по которым явно вычисляются искомые величины. Однако чаще всего поведение параметров описывается дифференциальными уравнениями в частных производных. Найти решение этих сложных задач можно только с использованием современных быстродействующих ЭВМ. Решение сложной математической задачи на ЭВМ включает в себя необходимые этапы выбора метода решения, создания алгоритма, разработки программы и ее тестирования. После этого можно применять разработанный пакет программ для решения нужной задачи. Даже для того, чтобы воспользоваться стандартной, т.е. уже готовой программой, нужно иметь представление о существующих методах решения, их преимуществах, недостатках и особенностях использования.
Все математические задачи классифицированы, т.е. объединены в некоторые группы. Для каждой группы задач существует набор стандартных методов, которые изучает специальный раздел математики – «Вычислительная математика» или «Методы вычислений».
Все методы решения уравнений можно разделить на два класса: точные и приближенные. В точных методах решение получают в виде формул за конечное число операций, но их можно применять только для решения уравнений специального вида.
В общем случае задачу можно решить только приближенно. Приближенные методы позволяют получить решение в виде бесконечной последовательности, сходящейся к точному решению. Использование ЭВМ выдвигает дополнительные требования к алгоритму нахождения как точного, так и приближенного решения: он должен быть устойчивым, реализуемым и экономичным. Устойчивость означает, что малые погрешности, внесенные в процессе решения, не приводят к большим ошибкам в конечном результате. Погрешности возникают из-за неточного задания исходных данных (неустранимые ошибки), из-за округления чисел, которое всегда имеет место при расчетах на ЭВМ, а также связаны с точностью используемого метода. Реализуемость алгоритма означает, что решение может быть получено за допустимое время. При этом надо иметь в виду, что время приближенного решения зависит от точности, с которой мы хотим получить решение. На практике точность выбирают с учетом реализуемости алгоритма на той ЭВМ, которую предполагается использовать для решения. Экономичным называется алгоритм, который позволяет получить решение с заданной точностью за минимальное количество операций и, следовательно, за минимальное расчетное время.
Данное пособие предназначено для ознакомления с основными методами, применяемыми для решения различных математических задач. Первым рассматриваемым классом задач является нелинейные алгебраические уравнения. Затем рассматриваются методы решения систем нелинейных и линейных уравнений. Пособие предусматривает получение студентами навыков построения двумерных и поверхностных графиков.
Каждая тема содержит теоретический материал и примеры использования методов для решения конкретных задач, описания основных вычислительных алгоритмов, тексты программ и описание стандартных функций пакета Mathcad, реализующих изученные вычислительные алгоритмы.
Для закрепления теоретического материала предусматривается выполнение лабораторных работ по основным рассматриваемым темам.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
В теоретической части рассматриваются вопросы реализации решения задач с помощью пакета Mathcad. Описываются простейшие конструкции программы, структура документа. Дается определение переменной и ее диапазона. Подробно рассматривается вопрос Решения уравнений средствами Mathcad.
Цель теоретической части: Дать представление о пакете Mathcad его структуре и внешнем виде. Ознакомиться с основными функциями в системе в этой системе. Уяснить предназначение этих функций. Понять для каких целей применяются данные функции.
Числа
Например: 123, -0.001, 15h, 15H, 12O, 12o, 2+3i
Числа, задаваемые в 16-ричной системе счисления, оканчиваются символом h (или H), в 8-ричной - символом o (или O).
Системные константы
· p
· e =2.718…
· ∞ =10^308
· i,j
Системные переменные
· TOL = 10^3 -точность
· ORIGIN =0 - начальный индекс вектора или матрицы
Переменные
Имена переменных могут содержать следующие символы:
· буквы - AaBbCcDdEe...
· цифры - 1234567890
· греческие буквы – σ, τ, ω, χ, π, ν, μ, λ
· специальные знаки - (знак подчеркивания), %
Замечание: Имя переменной начинается с буквы.
Выражение в Mathcadе есть совокупность имен переменных, чисел, функций, соединенных знаками операций и отношений.
Аргументами встроенных функций могут быть константы, переменные, функции, выражения.
Текстовые фрагменты
Текстовые фрагменты представляют собой куски текста, которые пользователь хотел бы видеть в своем документе. Существуют два вида текстовых фрагментов:
- текстовая область предназначена для небольших кусков текста — подписей, комментариев и т. п. Вставляется с помощью команды Вставка à Текстовый регион (Insert →”Text Region”)или комбинации клавиш Shift+"(двойная кавычка);
- текстовый абзац применяется в том случае, если необходимо работать с абзацами или страницами. Вставляется с помощью комбинации клавиш Shift+ Enter.
Графические области
Графические области делятся на три основных типа — двумерные графики, трехмерные графики и импортированные графические образы. Двумерные и трехмерные графики строятся самим Mathcad на основании обработанных данных.
Для создания декартового графика (рис.1):
- Установить визир в пустом месте рабочего документа.
- Выбрать команду(Insert→Graph) Вставка à График à Х-У график , или нажать комбинацию клавиш
- Shift+ @, или щелкнуть кнопку  панели Графики. Появится шаблон декартового графика.
панели Графики. Появится шаблон декартового графика.
- Введите в средней метке под осью Х первую независимую переменную, через запятую — вторую и так до 10, например х1, х2,
- Введите в средней метке слева от вертикальной оси Y первую независимую переменную, через запятую — вторую и т. д., например у1(х1), у2(х2), …, или соответствующие выражения.
- Щелкните за пределами области графика, что бы начать его построение.
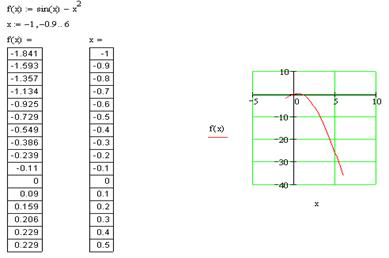
Рис. 1Пример табулирования функции с использованием
ранжированной переменной
Создание трехмерных графиков более подробно описано вметодических указаниях к лабораторной работе по этой теме
Рекомендации по использованию функции root
Для изменения точности, с которой функция root ищет корень, нужно изменить значение системной переменной TOL. Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, то функция root будет сходиться медленнее, но ответ будет более точен. Если два корня расположены близко друг от друга, следует уменьшить TOL, чтобы различить их.
Если функция f(x) имеет малый наклон около искомого корня, функция root(f(x), x) может сходиться к значению r, отстоящему от корня достаточно далеко. В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL.
Для выражения f(x) с известным корнем а нахождение дополнительных корней f(x) эквивалентно поиску корней уравнения h(x) = f(x)/(x — a). Подобный прием полезен для нахождения корней, расположенных близко друг к другу. Проще искать корень выражения h(x), чем пробовать искать другой корень уравнения f(x) = 0, выбирая различные начальные приближения.
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
vnxn + … + v2x2 + v1x + v0,
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения и возвращает сразу все корни, как вещественные, так и комплексные.
Polyroots(v)
Возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе v длины n + 1. Возвращает вектор длины n, состоящий из корней полинома.
Аргументы:
v — вектор, содержащий коэффициенты полинома.
Вектор v удобно создавать использую команду Символы à Коэффициенты полинома. рис. 5 иллюстрирует определение корней полинома средствами Mathcad.

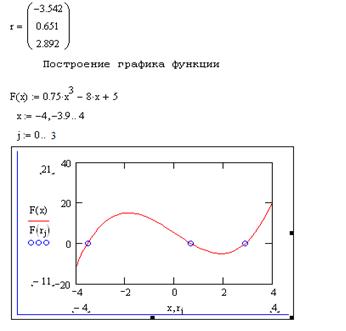
Рис. 5 Пример нахождения корней полинома
Решение систем уравнений
Mathcad дает возможность решать также и системы уравнений. Максимальное число уравнений и переменных равно 50. Результатом решения системы будет численное значение искомого корня.
Пример нахождения решений системы линейных уравнений
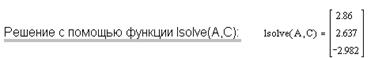




Как видно из анализа результатов, решения разными методами совпадают.
Использование блоков Given, Find. Minerr
для решения систм уравнений
Find(v1,v2,…,vn) – находит значение переменных для точного решения (решение реально существует, хотя и не является аналитическим),
Minerr(v1,v2,…,vn) – находит значение переменных для приближенного решения (находит максимальное приближение даже к несуществующему).
Эти функции могут применяться только после блока Given. Имена этих функций можно писать и строчными буквами. При вводе ограничительных условий необходимо использовать логические операторы: >, <, ³, £, ¹, =. Эти операторы вызываются с помощью палитры «Отношения». Рекомендуется после нахождения решения сделать проверку подстановкой.
Given – ключевое слово, открывающее блок решения систем уравнений (в котором обычно используются функции Find, Minerr, Maximize и Minimize)
Для решения системы уравнений необходимо выполнить следующее:
· Задать начальное приближение для всех неизвестных, входящих в систему уравнений. Mathcad решает систему с помощью итерационных методов.
· Напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений.
· Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >, ≤, и ≥.
· Введите любое выражение, которое включает функцию Find, например: а:= Find(х, у).
Find(var1,var2, …) значения var1, var2, …,дающие точные решения системы уравнений в блоке, объявленном директивой Given (число возвращаемых значений равно числу аргументов),который помимо решаемой системы уравнений, может содержать условия ограничения.
Пример решения системы нелинейных уравнений с использованием функции Find:
x:=0 y:=0
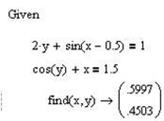
Внутри блока решения недопустимы следующие выражения:
· Ограничения со знаком ≠.
· Дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.
· Неравенства вида a < b < c.
Блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (рис.9).
Функция, которая завершает блок решения уравнений, может быть использована аналогично любой другой функции. Можно произвести с ней следующие три действия:
· Можно вывести найденное решение, напечатав выражение вида:
Find(var1, var2,…) =.
· Определить переменную с помощью функции Find:
a := Find(x) — скаляр, var := Find(var1, var2,…) — вектор.
Это удобно сделать, если требуется использовать решение системы уравнений в другом месте рабочего документа.
· Определить другую функцию с помощью Find
f(a, b, c, …) := Find(x, y, z, …).

Рис. 9. Решение систем уравнений в Mathcad
ПРАКТИЧЕСКАЯ ЧАСТЬ
Лабораторные работы направлены на получение навыков использования математических пакетов в решении различных математических и инженерных задачах, в представлении полученных результатов различными методами (табличном, графическом виде).
Все работы выполняются по вариантам, задаваемым преподавателем. После выполнения работы оформляется отчет.
Цель практической части:Научить студентов работе в системе Mathcad. Получить навыки решения уравнений разной сложности, использовать математические и статистические функции всистеме Mathcad.
Содержание отчета
- Название работы.
- Результаты выполнения заданий.
- Выводы по работе относительно используемых операторов, функций и полученных результатов.
Лабораторная работа №1
Табулирование функций и нахождение корней уравнений
в системе Mathcad
Подготовка к работе
По указанной литературе изучить:
- правила ввода текста, данных, переменных;
- задание функций пользователя;
- операторы присваивания;
- правила построения графиков и графические средства для работы с ними;
- правила вывода таблиц с результатами вычислений;
- состав и назначение элементов Math Palette (палитры математических символов).
Задание и порядок выполнения работы
- Создать в текстовой области заголовок документа "Вычисления в Mathcad".
- Задать выражение для расчета заданной переменной, выбранную из табл. 1. в соответствии с вариантом, для конкретного значения аргумента.
- Задать это выражение как функцию пользователя.
- Задать ранжированную переменную, изменяющуюся в пределах xo¸xn с шагом h=0.1. Рассчитать и вывести в виде таблицы значения функции при изменении аргумента в заданном интервале.
5. Для данной функции построить XY - график. Отформатировать его для наглядного представления заданной функции.
6. Построить график функции f(x) и приблизительно определить один из корней уравнения. Решить уравнение f(x)= 0 с точностью ε = 10 - 4 с помощью встроенной функции Mathcad root. Варианты заданий (Таблица 1);
Таблица 1
Варианты заданий
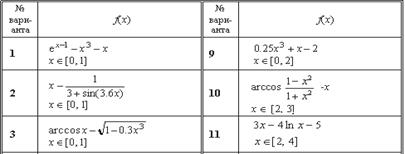
Продолжение таблицы 1
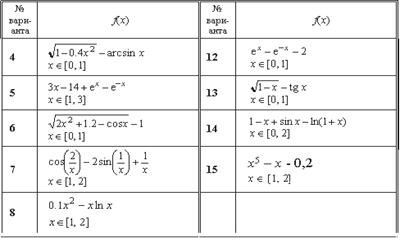
7. Найти корни полинома с помощью функции polyroots. Задать вектор V, содержащий коэффициенты полинома. Коэффициенты полинома найти с использованием символьной команды. Варианты заданий (Таблица 2)
Таблица 2
Варианты заданий
| № варианта | g(x) | № варианта | g(x) |
| x4 – 2x3+x2 – 12x+20 | x4+x3 – 17x2 – 45x – 100 | ||
| x4+6x3+x2+x2 – 4x – 60 | x4 – 5x3 +2x2 –15x+50 | ||
| x4 – 14x3 – 40x – 75 | x4 – x3 –x2 – 20x+25 | ||
| x4 – x3+x2 – 11x+10 | x4+5x3+7x2 – 5x+95 | ||
| x4 – x3+13x2 – 31x + 25 | x4 – 7x3+17x2+x – 20 | ||
| x4+7x3+9x2+13x – 30 | x4+10x3+36x2+70x+75 | ||
| x4+3x3 – 23x2 – 55x – 150 | x4+9x3+39x2+59x+60 | ||
| x4 – 6x3+4x2–10x+75 |
Методические указания
Пример выполнения задания лабораторной работы
Чтобы определить начальное приближение по хвоспользуемся графиком. По команде Format →Graph → Trace, выплывет окно, показанное на рис. 10, по нему определите приближенное значение х,предварительно нужно щелкнуть по точке пересечения графика функции с осью абсцисс.
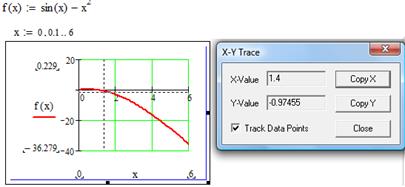
Рис. 10 Определение приближенного значения х
По графику обнаружено начальное приближение х= 1.4
Изменение системного параметра TOL (рис.11). Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL:=0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите команду Математика à Параметры… à Переменныеà Допуск сходимости (TOL), (Toolsà Workscheetà Convergence Tolerance(TOL) – в англоязычном Mathcad)
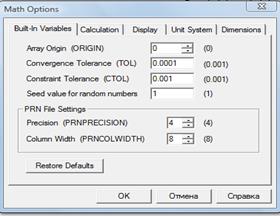
Рис. 11 Окно системных параметров
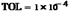 Установленозначение
Установленозначение
Контрольные вопросы
1. Поясните структуру окна системы Mathcad.
2. Какие приёмы создания текстовой области Вы знаете?
3. Перечислите приоритетность выполнения операций в выражениях.
4. Какие типы данных используются в системе Mathcad?
5. Дайте понятие идентификатора.
6. Какие требования предъявляются к идентификаторам?
7. Дайте понятие переменной.
8. Как задать переменную в системе Mathcad?
9. Что такое ранжированная переменная?
10. Для решения, каких задач используется ранжированная переменная?
11. Дать понятие функции пользователя?
12. Назовите оператор присвоения системы Mathcad?
13. Назовите оператор вывода системы Mathcad?
14. Как вывести результаты вычислений в виде таблиц?
15. Как создать и отредактировать XY - график?
Лабораторная работа №2
Функции условных выражений
Подготовка к работе
По указанной литературе изучить:
‒ категории функций;
‒ операции отношений;
‒ правила записи функции условных выражений;
‒ состав палитр Evaluation and Boolean (Отношения) .
Задание и порядок выполнения работы
1 Задать условную функцию с использованием функции if и условий. Варианты заданий в таблице 3
2 Задать эту функцию, используя операторы if и otherwise из палитры программирования
Выведите таблицы результатов и сравните их между собой.
Таблица 3
Варианты заданий
| № | Функция | x=[ ], a, b |
| 1. | 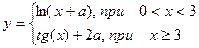 | x=[0 ..5] a=1.5 |
| 2. | 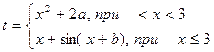 | x=[-2 ..2] a=5 b=2 |
| 3. | 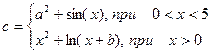 | x=[-5 ..5] a=2.5 b=3 |
| 4. | 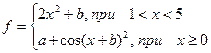 | x=[-4 ..4] a=3 b=1.5 |
| 5. | 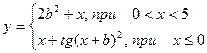 | x=[-3 ..4] a=6 b=3.5 |
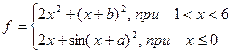 | x=[-2 .. 4] a=3 b=4 | |
| 6. | 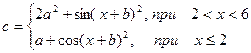 | x=[-4 5] a=2 b=1.5] |
Продолжение таблицы 3
| 7. | 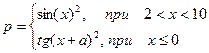 | x=[-5..5] a=3 b=4.5 |
| 8. | 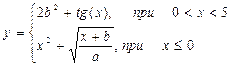 | x=[0..7] a=4 b=6 |
| 9. | 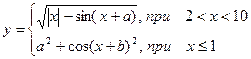 | x=[-1 .. 6] a=3 b=5 |
| 10. | 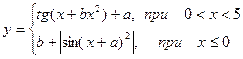 | x=[-2..7] a=2 b=4 |
| 11. | 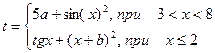 | x=[-1 5] a=3 b=8 |
| 12. | 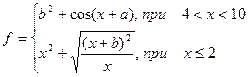 | x=[1 .. 8] a=2 b=4 |
| 13. | 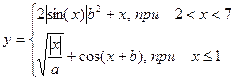 | x=[0…9] a=1.5 b=6 |
Методические указания
Для создания условных выражений можно использовать условия, функцию if , а также операторы программирования if и otherwise.
С помощью функции с элементами сравнения можно моделировать другие функции. Пример функции, описывающей импульсные сигналы различного вида, приведен на рис. 12.
Пример применения функции if
Пусть требуется найти значение функции
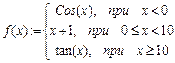 для x=7.
для x=7.
Mathcad-документ может быть составлен следующим образом:
f(x):= if(x<0,cos(x),if(x<10,x+1,tan(x))) f(7)= 8
Замечание: Функция f(x) может быть задана и таким образом:
f(x):=(x<0) cos(x)+(x>0) (x<10) (x+1)+(x>10) tan(x).
Для создания условия в Mathcad предусмотрены также операторы в палитре программирования if и otherwise (если, иначе).
На рис.12 приведен пример моделирования выпрямления функции sin(x).

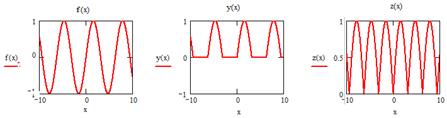
Рис. 12 Пример моделирования одно и двух–полупериодного
выпрямления функции
Контрольные вопросы
1. Какие виды встроенных функций имеются в системе Mathcad?
2. Как пользоваться встроенными функциями?
3. Запись условий в системе Mathcad.
4. Как записать условную функцию, используя условные выражения?
5. Синтаксис функции if, её аргументы?
6. Значения условного выражения при истинности условия?
7. Значения условного выражения при ложности условия?
Лабораторная работа №3
Функции для обработки векторов и матриц
Подготовка к работе
По указанной литературе изучить
- палитру Vector and Matrix (Векторы и матрицы) и назначение элементов этих палитр;
- ввод, вывод и обработку одномерных и двумерных массивов данных;
- приемы работы с массивами данных в Mathcad;
- векторные и матричные операторы;
- векторные и матричные функции;
Задание и порядок выполнения работы
1 Выполнить сортировку для векторов (Таблица 4)
2 Выполнить сортировку для матриц (Таблица 5).
3 Вычислить вектор VE собственных значений матрицы М .
Таблица 4
Варианты заданий
| № вар. | Заданный вектор | № вар. | Заданный вектор |
| V=[3, 2, 4, 5] | V=[7, 18, 3, 11] | ||
| V=[7, 8, 9, 5] | V=[1, 5, 3, 9] | ||
| V=[12, 14, 7, 11] | V=[24, 9, 12, 27] | ||
| V=[6, 8, 10, 15] | V=[9, 3, 17, 11] | ||
| V=[3, 9, 12, 14] | V=[4, 15, 2, 19] | ||
| V=[7, 9, 11, 13] | V=[11, 17, 1, 13] | ||
| V=[5, 7, 8, 12] | V=[5, 9, 15, 2] | ||
| V=[23, 25, 7, 19] |
Таблица 5
Варианты заданий
| № вар | Исходная матрица 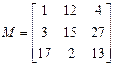 | № вар | Исходная матрица 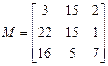 |
| Отсортировать по 1 столбцу. Вывести этот столбец | Отсортировать по 1 столбцу. Вывести этот столбец | ||
| Отсортировать по 1 строке. Вывести эту строку | Отсортировать по 1 строке. Вывести эту строку | ||
| Отсортировать по 2 столбцу. Вывести этот столбец | Отсортировать по 2 столбцу Вывести этот столбец |
Продолжение таблицы 5
| Отсортировать по 2 строке. Вывести эту строку | Отсортировать по 2 строке. Вывести эту строку | ||
| Отсортировать по 3 столбцу Вывести этот столбец | Отсортировать по 3 столбцу Вывести этот столбец | ||
| Отсортировать по 3 строке. Вывести эту строку | Отсортировать по 3 строке. Вывести эту строку |
Методические указания
Вывод элементов матрицы А и элементов вектора В и Х1
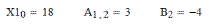
Транспонирование вектора Х
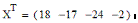
Исходный вектор Прямая сортировка Реверс сортировки
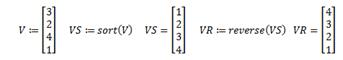
Исходная матрица Сортировка по первой строке Сортировка по первому столбцу
Начальный индекс столбца и строки ORIGIN = 0
Вывод второго столбца матрицы Вывод второй строки матрицы

Рис. 10 Примеры применения векторных и матричных функций
Контрольные вопросы
1. Какие операции можно производить с матрицами и векторами в Mathcad?
2. Назовите элементы палитры Vector and Matrix (Векторы и матрицы) и их назначение.
3. Назовите операции над матрицами и векторами в Mathcad?
4. Назовите функции сортировки векторов и матриц.
5. Как вывести нужный элемент массива?
6. Как вывести заданный столбец матрицы?
7. Как вывести заданную строку матрицы?
8. Назовите функцию вычисления следа матрицы, поясните, что называется следом матрицы.
Лабораторная работа №4
Решение систем линейных и нелинейных уравнений
Подготовка к работе
По указанной литературе изучить
- способы решения систем линейных уравнений в Mathcad;
- способы решения нелинейных уравнений в Mathcad
- функция для решения системы линейных уравнений методом Гаусса.
Задание и порядок выполнения работы
1. Решить систему линейных уравнений (Таблица 6):
- используя функцию Find, решить уравнение в символьном виде;
- матричным способом;
- используя функцию lsolve.
2. Решить систему нелинейных уравнений (Таблица 7)
- приближенно графически;
- используя функцию Find
- используя функцию Minerr.
Таблица 6
Варианты заданий
| № вар. | Система линейных уравнений | № вар. | Система линейных уравнений |
| 1. | 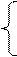 2x1 +x2 + 2x3+3x4=8 3x1+3x3=6 2x1 – x2 + 3x4=4 x1+2x2 – x3 + 2x4=4 2x1 +x2 + 2x3+3x4=8 3x1+3x3=6 2x1 – x2 + 3x4=4 x1+2x2 – x3 + 2x4=4 | 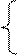 x1 +2x2 + 8x3+2x4= 114 8x1+x2 + 2x3 + x4=52 x1 + 5x2 + x3 =72 x1 – 12x2 +5x3 + x4= 97 x1 +2x2 + 8x3+2x4= 114 8x1+x2 + 2x3 + x4=52 x1 + 5x2 + x3 =72 x1 – 12x2 +5x3 + x4= 97 | |
| 2. | 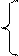 x1 +2x2 + 3x3+4x4=22 2x1+3x2+ x3 + 2x4=17 2x1 + x2 + x3 – 7x4=8 x1 – x3 + 3x4= – 7 x1 +2x2 + 3x3+4x4=22 2x1+3x2+ x3 + 2x4=17 2x1 + x2 + x3 – 7x4=8 x1 – x3 + 3x4= – 7 | 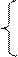 6x1 - 4x2 + 12x3 - 2x4= 132 2x1+x2 + 9x3 + 5x4=118 3x1 - 2x2 - 2x3 - x4=7 x1 - 12x2 +2x3 - x4= 17 6x1 - 4x2 + 12x3 - 2x4= 132 2x1+x2 + 9x3 + 5x4=118 3x1 - 2x2 - 2x3 - x4=7 x1 - 12x2 +2x3 - x4= 17 | |
| 3. | 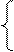 2x1 +x2 - 5x3+x4= – 4 x1+3x2 - 6x4=9 x1 – x2 + 3x3=6 x1+4x2 –7x3 + 2x4= – 2 2x1 +x2 - 5x3+x4= – 4 x1+3x2 - 6x4=9 x1 – x2 + 3x3=6 x1+4x2 –7x3 + 2x4= – 2 | 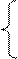 x1 - 2x2 - x4= 86 5x1 + 2x3 - 3x4=88 7x1 - 3x2 + 7x3 +2x4=146 3x1 – 7 x2 +6x3 + 3x4= 89 x1 - 2x2 - x4= 86 5x1 + 2x3 - 3x4=88 7x1 - 3x2 + 7x3 +2x4=146 3x1 – 7 x2 +6x3 + 3x4= 89 | |
| 4. | 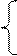 x1 +2x2 + 3x3+2x4= 24 2x1+3x2 + 4x3 + x4=32 3x1 + 4x2 + x3 +2x4=26 4x1+2x2 +x3 + 3x4= 24 x1 +2x2 + 3x3+2x4= 24 2x1+3x2 + 4x3 + x4=32 3x1 + 4x2 + x3 +2x4=26 4x1+2x2 +x3 + 3x4= 24 | 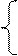 x1 - 2x2 - 8x4= – 8 x1+5x2 - 7x3 + 5x4= – 12 x1 + x2 - 5x3 +2x4= – 15 3x1 – x2 + 3x4= 9 x1 - 2x2 - 8x4= – 8 x1+5x2 - 7x3 + 5x4= – 12 x1 + x2 - 5x3 +2x4= – 15 3x1 – x2 + 3x4= 9 |
Продолжение таблицы 6
| 5. | 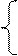 2x1 +x2 + 5x3 - x4= 14 7x2 - x3 + 3x4= – 5 4x1 + x2 + 2x3 =16 x1+5x2 +2x3 - 7x4= – 13 2x1 +x2 + 5x3 - x4= 14 7x2 - x3 + 3x4= – 5 4x1 + x2 + 2x3 =16 x1+5x2 +2x3 - 7x4= – 13 | 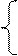 2x1 +2x2 + 7x3+x4= 14 – 2x2 + 3x3 + x4=19 2x1 + 2x2 + x3 +x4=22 3x1 - 5x2 +x3 - x4= 32 2x1 +2x2 + 7x3+x4= 14 – 2x2 + 3x3 + x4=19 2x1 + 2x2 + x3 +x4=22 3x1 - 5x2 +x3 - x4= 32 | |
| 6. | 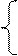 4x1 +7x2 + x3 - 4x4= 12 x1 + 6x3 + x4=21 x1 + 4x2 + 6x4=16 2x2 +4x3 + x4= 15 4x1 +7x2 + x3 - 4x4= 12 x1 + 6x3 + x4=21 x1 + 4x2 + 6x4=16 2x2 +4x3 + x4= 15 | 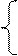 8x1 - x2 + 7x3+5x4= 156 2x1+x2 - 3x3 - x4= – 17 11x1 + 4x2 + x3 =176 x1 - x2 - 3x3 - 4x4= – 25 8x1 - x2 + 7x3+5x4= 156 2x1+x2 - 3x3 - x4= – 17 11x1 + 4x2 + x3 =176 x1 - x2 - 3x3 - 4x4= – 25 | |
| 7. | 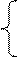 7x1 +7x2 - 3x3+2x4= 8 2x1+4x2 + 5x3 + 8x4=42 2x1 + 2x2 + 2x3 +2x4=28 2x1 - 2x3 - x4= – 2 7x1 +7x2 - 3x3+2x4= 8 2x1+4x2 + 5x3 + 8x4=42 2x1 + 2x2 + 2x3 +2x4=28 2x1 - 2x3 - x4= – 2 | 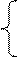 6x1 - 9x2 + 7x3= 75 7x1 - 3x3 - x4= – 35 9x2 + 7x3 +x4=97 5x1 - 9x2 +x3 + 6x4= 45 6x1 - 9x2 + 7x3= 75 7x1 - 3x3 - x4= – 35 9x2 + 7x3 +x4=97 5x1 - 9x2 +x3 + 6x4= 45 | |
| 8. | 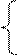 6x1 - 7x2 + 5x3+2x4= 64 5x1+5x2 - 14x3 = – 27 4x1 + 3x2 – 11x4=6 x1+2x2 +2x3 + x4= 42 6x1 - 7x2 + 5x3+2x4= 64 5x1+5x2 - 14x3 = – 27 4x1 + 3x2 – 11x4=6 x1+2x2 +2x3 + x4= 42 |
Таблица 7
Варианты заданий
| № | Функции F1(x), F2(x) интервал x=[ ], шаг h | № | Функции F1, F2 интервал x=[ ], шаг h |
| 1. | F1(x)= – 1.5x3 – 5x2+3x+45 F2(x)= – 75│cos(x)│ x=[ – 10..10] h=0.3 | 9. | F1(x)=2.5x3 + 2.9x2+x+17 F2(x)= 20sin(x2) x=[ – 20..20] h=0.2 |
| 2. | F1(x)=5x3 + x2+12x+9 F2(x)= 25│sin(x)│(1) x=[ – 10..10] h=0.2 | 10. | F1(x)= – 3.5x3 +10x+65 F2(x)= 55│cos(x)│ x=[ – 10..10] h=0.3 |
| 3. | F1(x)=– 0.5x3 + 5x2+5x – 15 F2(x)= – 15│tg(x)│ x=[ – 10..10] h=0.1 | 11. | F1(x)=7.5x3 – x2 – 13x +35 F2(x)= 10│cos(x)│ x=[ – 10..10] h=0.3 |
| 4. | F1(x)=x3 + 2x2+15x – 27 F2(x)= 53│cos(x)│ x=[ – 15..15] h=0.5 | 12. | F1(x)=– 3x3 + x2 – 20x – 7 F2(x)= 20│tg(x)│ x=[ – 10..10] h=0.3 |
| 5. | F1(x)=4.6x2+10x + 30 F2(x)= 40sin(x) x=[ – 10..10] h=0.3 | 13. | F1(x)=6.5x3 – 9x2+7x – 19 F2(x)= – 15│tg(3x)│ x=[ – 15..15] h=0.1 |
| 6. | F1(x)=– 4.5x3 + 3x2 – 4 x+60 F2(x)= 90│cos(x)│ x=[ – 20..20] h=0.4 | 14. | F1(x)=– 8.5x3 – 2x2+20x+5 F2(x)= – 35│cos(x)│ x=[ – 10..10] h=0.2 |
| 7. | F1(x)=– 7.5x3 + 16x2+54 F2(x)= – 45│cos(2x)│ x=[ – 25..20] h=0.2 | 15. | F1(x)= – 15x2+9x+70 F2(x)= 5│sin(x)│ x=[ – 20..20] h=0.5 |
| 8. | F1(x)=– 5x3 +13x+40 F2(x)= 50cos(3x) x=[ – 10..10] h=0.5 |
Методические указания
Решить систему линейных уравнений: 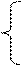
4x1 +x2 + x3+3x4=25
3x1 – x2+3x3=16
2x1 – 2x2 + 3x4=– 4
x1+2x2 – x3 + 2x4=4
Матричным способом X:=A-1 × B, где А- матрица, составленная из коэффициентов перед неизвестными, В – вектор свободных членов, X – вектор корней x1, x2, x3 …;
С помощью встроенной функции lsolve(А,В).
Проверить результаты решения непосредственной подстановкой полученных корней х1, х2, х3 в одно из заданных уравнений.
Решение в матричной форме
А – матрица коэффициентов системы при неизвестных
В – вектор свободных членов
Решение системы в матричной форме A × Х:=В, где Х – вектор корней системы линейных уравнений.
Результат решения системы линейных уравнений Х=(х1,х2,х3,х4)
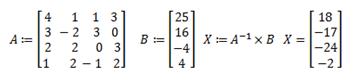
Результат решения системы линейных уравнений Х1=(x1,х2,х3,х4)
Результат решения системы линейных уравнений с использованием функции lsolve

Проверка решения системы линейных уравнений
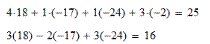
Подготовка к работе
По указанной литературе изучить:
- задание функций пользователя;
- операторы присваивания;
- состав палитры Programming Palette (Программирование);
- программирование вложенных условных выражений;
- возможности системы программирования для организации циклов с известным числом повторений с помощью оператора for…;
- возможности системы программирования для организации циклов с неизвестным числом повторений с помощью операторов while…;
Задание и порядок выполнения работы.
1. Рассчитать значения заданной функции с использованием программного блока. Предусмотреть ввод данных с использованием оператора как локального, так и глобального присваивания. Задание в таблице 8. Построить график заданной функции с шагом 0,3.
2. Используя оператор условных выражений, вычислить функцию, выбранную из табл. 2 согласно варианту. Протестировать все ветви разветвляющегося процесса: вывести несколько з
