Решение задачи 7 контрольной работы № 1

Задача. Отношения R и S заданы в виде таблиц (рис. 1.19, а). Совместимы ли эти отношения? Записать обозначение проекции R на список 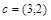и выполнить эту операцию. Записать обозначение соединения отношений R и S по условию F – “A₂³B₁” и выполнить эту операцию.

Решение. Степень отношения R равна 3 (три столбца в таблице), степень отношения S равна 2 (два столбца), значит, отношения R и S несовместимы и над ними нельзя выполнять операции пересечения, объединения, разности.

	R S pCR A1 A2 A3 B1 B2 C1 C2 D1 D2 D3 D4 D5 a b c b k c b a b c b k k m t c m t m k m t b k b a d d t d a k m t c m k m t d l а) б) в) Рис. 1.19. Операции над отношениями R и S а) данные отношения; б) проекция отношения R на список c =(3,2); в) соединение отношений R и S по условию F= ”A2³ B1”

Обозначение операции проекции 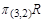. Чтобы выполнить эту операцию, выписываем третье и второе поле всех записей в новую таблицу (вычеркнули столбец 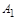, столбцы 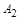и 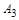поменяли местами); одинаковых строк нет (рис. 1.19, б).

Обозначение операции соединения - .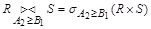

Результат операции 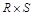– девять записей (к каждой строке таблицы R приписываем строку таблицы S). Вычеркиваем строки, не удовлетворяющие условию 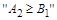, т.е. строки, второй элемент которых стоит в алфавите раньше четвертого ( рис. 1.19, в).

1.4.1. Контрольные вопросы и упражнения

1. При каких условиях таблица является аналогом n-арного отношения?

2. Что называется степенью такого отношения?

3. Какие отношения в реляционной алгебре называются совместимыми?

4. Составьте конкатенацию записей “ пас ” и “ тор ”.

5. Отношение R имеет степень 3, отношение S – 4. Какую степень будет иметь отношение ?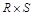

6. Операция проекции отношения R на список столбцов обозначается _____________________ .

7. Как выполняется операция селекции отношения R по условию F?

8. Какие операции и в каком порядке нужно выполнить:

?

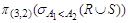Конечные и бесконечные множества

Равномощные множества

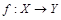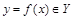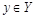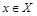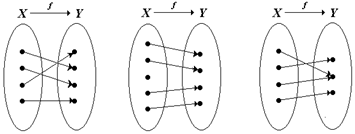
Напомним, что отображение является биекцией (см.1.2.1) тогда и только тогда, когда каждый элемент х множества Х имеет единственный образ , а каждый элемент имеет единственный прообраз , т.е. 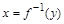. Так, соответствие между множествами X и Y на рис. 1.20, а является биекцией, а на рис. 1.20, б, в – не является биекцией (объясните почему).

а) б) в)

Рис. 1.20. Соответствие множеств X и Y

а) биективное;

б) в) не биективное

Определение. Будем говорить, что множества X и Yравномощны, если существует биекция множества X на множество Y.

Пример. Покажем, что множества 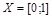и 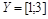равномощны. Действительно, можно установить биекцию 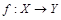, например, по закону 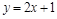(рис. 1.19, а). Биекцию между множествами X и Y можно установить и геометрически (рис. 1.19, б). Через левые концы отрезков проведена прямая l , через правые – прямая m. Точка пересечения прямых l и m обозначена М. Из точки М проводим лучи, пересекающие оба отрезка; при этом точке пересечения с лучом на первом отрезке соответствует единственная точка пересечения с лучом на втором отрезке (и наоборот).

Классы равномощных множеств

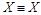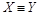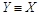Введенное в 1.4.1 отношение равномощности является отношением эквивалентности “ º “. В самом деле, оно рефлексивно: для каждого множества Х справедливо (Х равномощно Х), так как существует тождественное отображение множества Х на множество Х. Это отношение симметрично: если существует биекция X на Y , то обратное отображение также является биекцией (если , то ). 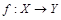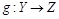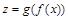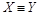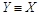Отношение транзитивно: если существует биекция и существует биекция , то соответствие отображает X на Z биективно (если и , то ).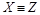

По свойству отношения эквивалентности (см. 1.2.5) получаем разбиение всех множеств на непересекающиеся классы равномощных множеств. Каждому классу присвоим название - кардинальное число. Таким образом, кардинальное число – это то общее, что есть у всех равномощных множеств. Обозначим кардинальное число множества 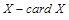или ½Х½. Пустое множество имеет кардинальное число 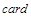Æ =0; для всех конечных множеств кардинальное число совпадает с количеством элементов множества; а для обозначения кардинального числа бесконечных множеств используется буква À (алеф). Понятие кардинального числа (мощности множества) обобщает понятие “ количество элементов ” на бесконечные множества.