Свойства операций сложения векторов и умножения вектора на скаляр
1.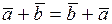 | 6. 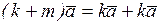 |
2. 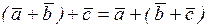 | 7. 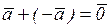 |
3. 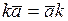 | 8. 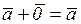 |
4. 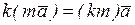 | 9. 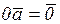 |
5. 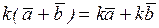 | 10. 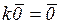 |
Векторы 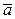 и
и 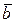 , лежащие на параллельных прямых (на одной прямой) называются коллинеарными.
, лежащие на параллельных прямых (на одной прямой) называются коллинеарными.
 или
или 
Если векторы 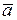 и
и 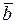 заданы своими координатами:
заданы своими координатами:
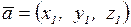 и
и 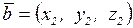 , то выполняется
, то выполняется
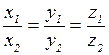 .
.
Это условие коллинеарности векторов.
Замечание 1:Векторы 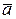 и
и 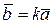 – коллинеарны.
– коллинеарны.
Векторы 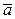 ,
, 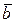 и
и 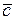 , лежащие в параллельных плоскостях (в одной плоскости) называются компланарными.
, лежащие в параллельных плоскостях (в одной плоскости) называются компланарными.
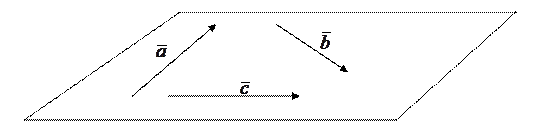
Если векторы 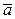 ,
, 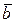 и
и 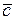 заданы своими координатами:
заданы своими координатами:
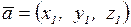 ,
, 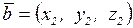 и
и 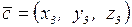 , то выполняется
, то выполняется
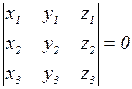 .
.
Это условие компланарности векторов.
Скалярным произведением векторов 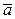 и
и 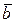 называется число, находимое по формуле:
называется число, находимое по формуле:
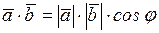 , где
, где 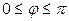 – угол между векторами
– угол между векторами 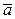 и
и 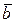 .
.
Если векторы 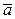 и
и 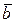 заданы своими координатами:
заданы своими координатами:
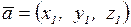 и
и 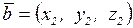 , то скалярное произведение векторов
, то скалярное произведение векторов
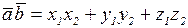 .
.
Например: 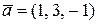 ,
, 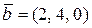 .
.
Тогда 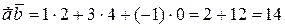
Векторы 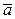 и
и 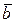 называются ортогональными, они лежат на перпендикулярных прямых.
называются ортогональными, они лежат на перпендикулярных прямых.
Замечание 2:Ненулевые векторы 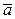 и
и 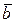 – ортогональны тогда и только тогда, когда
– ортогональны тогда и только тогда, когда 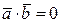 .
.
Если векторы 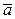 и
и 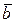 заданы своими координатами:
заданы своими координатами: 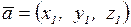 и
и 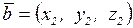 , то ортогональными они будут тогда и только тогда, когда
, то ортогональными они будут тогда и только тогда, когда
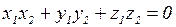 .
.
Это условие ортогональности векторов.
Длина вектора 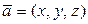 находится по формуле:
находится по формуле:
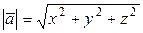 .
.
Например: 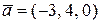 .
.
Тогда 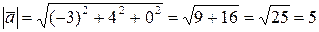 .
.
Если начало вектора – точка 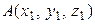 , а конец его – точка
, а конец его – точка 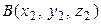 , то координаты вектора
, то координаты вектора
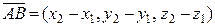 ,
,
и его длина находится по формуле:
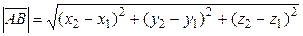 .
.
По этой же формуле находится длина вектора 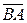 , расстояние между точками А и В.
, расстояние между точками А и В.
Например: 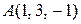 ,
, 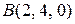 .
.
Тогда 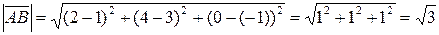 .
.
Координаты середины отрезка АВпри 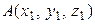 и
и 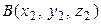 , найдутся по формуле:
, найдутся по формуле:
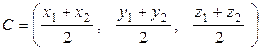 .
.
Например: 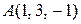 ,
, 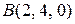 .
.
Тогда 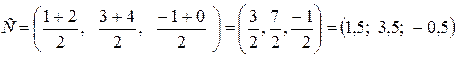
Векторным произведениемвекторов 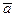 и
и 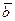 называется вектор
называется вектор 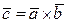 , который ортогонален векторам
, который ортогонален векторам 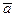 и
и 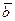 , составляет с ними правую тройку, модуль которого находится по формуле
, составляет с ними правую тройку, модуль которого находится по формуле 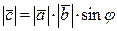 и численно равен площади параллелограмма, построенного на этих векторах.
и численно равен площади параллелограмма, построенного на этих векторах.
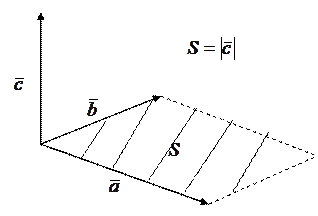
Если векторы 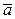 и
и 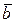 заданы своими координатами:
заданы своими координатами:
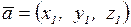 и
и 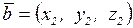 , или
, или
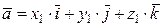 ,
,
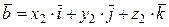 ,
,
тогда
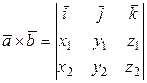 .
.
Например: 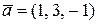 ,
, 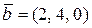 .
.
Тогда
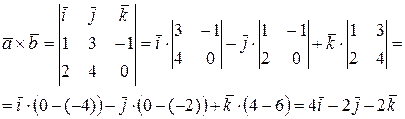
Свойства векторного произведения
1.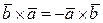 ;
;
2. 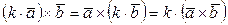 ;
;
3. 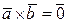 ,если
,если 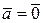 ,
, 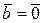 или
или 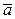 и
и 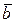 – коллинеарны;
– коллинеарны;
4. 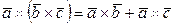 .
.
Смешанным произведениемвекторов 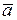 ,
, 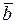 и
и 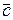 называется результат скалярного произведения вектора
называется результат скалярного произведения вектора 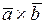 на вектор
на вектор 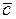 , то
, то 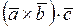 .
.
Свойства смешанного произведения
1. Смешанное произведение не изменяется, если поменять местами знаки векторного и скалярного произведения, то есть 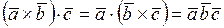 .
.
2. Модуль 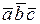 равен объему параллелограмма, построенного на этих векторах.
равен объему параллелограмма, построенного на этих векторах.
3. 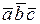 = 0, если, хотя бы один из множителей равен нулевой, любые два вектора коллинеарны, все три вектора компланарны.
= 0, если, хотя бы один из множителей равен нулевой, любые два вектора коллинеарны, все три вектора компланарны.
4. 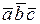 не изменяется при циклической перестановке сомножителей:
не изменяется при циклической перестановке сомножителей: 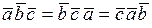 .
.
5. При перестановке местами двух сомножителей 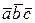 меняет знак:
меняет знак:
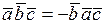 ;
; 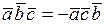 ;
; 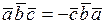 .
.
Если векторы 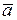 ,
, 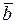 и
и 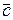 заданы своими координатами
заданы своими координатами 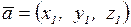 ,
, 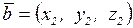 и
и 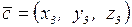 или
или
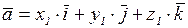 ,
,
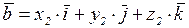 ,
,
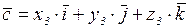
тогда
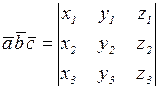 .
.
Например: 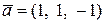
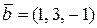 ,
, 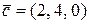 .
.
Тогда
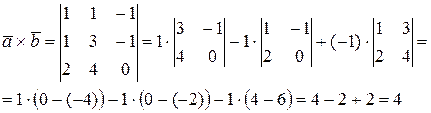
Замечание 3.Объем V треугольной призмы, построенной на векторах 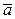 ,
, 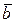 и
и 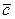 находится по формуле:
находится по формуле:
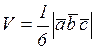 .
.
ПРЯМАЯ НА ПЛОСКОСТИ
Вопросы
1. Уравнение прямой на плоскости с угловым коэффициентом.
2. Уравнение прямой с угловым коэффициентом, проходящей через данную точку.
3.Уравнение прямой, проходящей через две данные точки.
4. Уравнение прямой, проходящей через данную точку параллельно данному вектору.
5. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
6. Уравнение прямой в отрезках.
7. Общее уравнение прямой.
8. Расстояние от точки до прямой.
Прямая – это линия на плоскости, точки которой 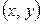 удовлетворяют уравнению:
удовлетворяют уравнению:
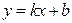 . (1)
. (1)
Коэффициент 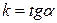 называется угловым коэффициентом прямой. Он равен тангенсу угла наклона прямой к положительному направлению оси ОХ (рис.1). Коэффициент b равен координате точки, в которой прямая пересекает ось ОY.
называется угловым коэффициентом прямой. Он равен тангенсу угла наклона прямой к положительному направлению оси ОХ (рис.1). Коэффициент b равен координате точки, в которой прямая пересекает ось ОY.

Рис 1.
Помимо уравнения (1) – уравнения прямой с угловым коэффициентом, существуют другие уравнения прямой.
Уравнение прямой с угловым коэффициентом k, проходящей через данную точку 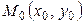 (рис 2.) имеет вид:
(рис 2.) имеет вид:
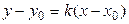 . (2)
. (2)
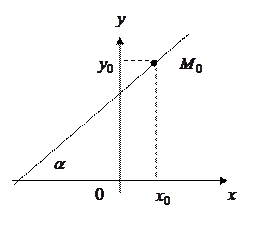
Рис 2.
Уравнение прямой, проходящей через две данные точки 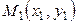 и
и 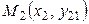 (рис 3.) имеет вид:
(рис 3.) имеет вид:
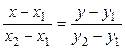 . (3)
. (3)
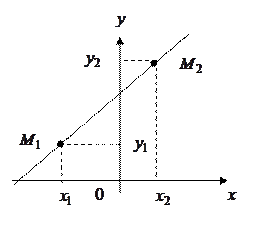
Рис 3.
Уравнение прямой, проходящей через данную точку 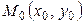 , параллельно данному вектору
, параллельно данному вектору 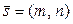 (рис 4.) имеет вид:
(рис 4.) имеет вид:
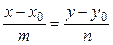 . (4)
. (4)
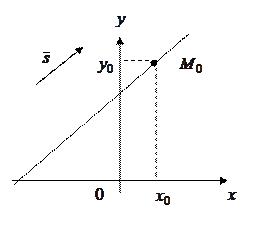
Рис 4.
Уравнение прямой, проходящей через данную точку 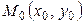 , перпендикулярно данному вектору
, перпендикулярно данному вектору 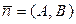 (рис 5.) имеет вид:
(рис 5.) имеет вид:
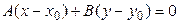 . (5)
. (5)
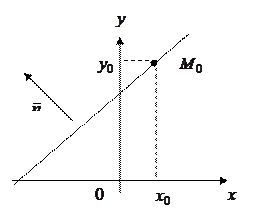
Рис.5
Уравнение прямой в отрезках (рис 6.) имеет вид:
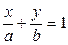 . (6)
. (6)
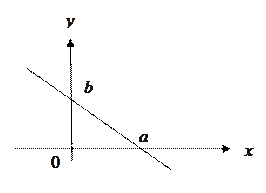
Рис 6.
Общее уравнение прямой имеет вид:
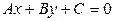 . (7)
. (7)
Замечание:
Все уравнения прямой могут быть приведены к общему уравнению прямой.
Расстояние от точки 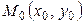 до прямой
до прямой 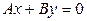 , заданной общим уравнением находится по формуле:
, заданной общим уравнением находится по формуле:
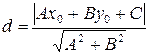 . (8)
. (8)
Например:
Задано общее уравнение прямой: 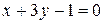 . Найти расстояние от точки
. Найти расстояние от точки 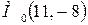 до этой прямой.
до этой прямой.
Тогда 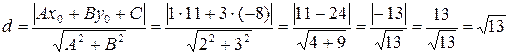 .
.
ПРЯМЫЕ И ПЛОСКИСТИ В 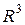
Вопросы
1. Общее уравнение плоскости.
2. Частные случаи уравнения плоскости.
3. Уравнение плоскости, проходящей через данную точку 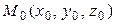 , перпендикулярно данному вектору
, перпендикулярно данному вектору 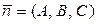 .
.
4. Как узнать, принадлежит ли произвольная точка плоскости.
5. Расстояние от точки до плоскости.
6. Взаимное расположение плоскостей.
7. Уравнение прямой в 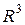 , проходящей через данную точку
, проходящей через данную точку 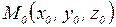 , параллельно данному вектору
, параллельно данному вектору 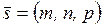 .
.
8. Уравнение прямой в 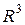 , проходящей через две данные точки
, проходящей через две данные точки 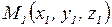 и
и 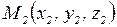 .
.
Плоскостьюназывается поверхность, все точки которой удовлетворяют общему уравнению плоскости:
Ax + By + Cz + D = 0,
где А, В, С – координаты вектора 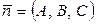 – вектор нормали к плоскости, т. е. вектор, перпендикулярный плоскости.
– вектор нормали к плоскости, т. е. вектор, перпендикулярный плоскости.
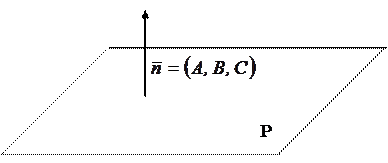
Возможны следующие частные случаи:
А = 0 – плоскость параллельна оси Ох;
В = 0 – плоскость параллельна оси Оу;
С = 0 – плоскость параллельна оси Оz;
D = 0 – плоскость проходит через начало координат;
А = В = 0 – плоскость параллельна плоскости хОу
А = С = 0 – плоскость параллельна плоскости хОz
В = С = 0 – плоскость параллельна плоскости yOz
А = D = 0 – плоскость проходит через ось Ох
В = D = 0 – плоскость проходит через ось Оу
С = D = 0 – плоскость проходит через ось Oz
А = В = D = 0 – плоскость совпадает с плоскостью хОу
А = С = D = 0 – плоскость совпадает с плоскостью xOz
В = С = D = 0 – плоскость совпадает с плоскостью yOz
| Например: | 1. 3x + 4y = 0 | проходит через ось ОZ, так как С=о, D=0 |
| 2. x + 4y – 5z = 0 | проходит через начало координат, так как D=0 | |
| 3. у – 5 = 0 | параллельна координатной плоскости XOZ, так как A=B=0 | |
| 4. 3x –z = 0 | проходит через ось ОУ, так как В=D=0 | |
| 5. 4y – 5z + 6 = 0 | параллельна оси ОХ, так как А=0 |
Уравнение плоскости, проходящей через данную точку, перпендикулярно данному вектору имеет вид:
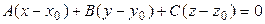
Здесь вектор 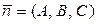 – нормаль к плоскости Р; точка
– нормаль к плоскости Р; точка 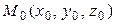 – точка, через которую проходит плоскость Р.
– точка, через которую проходит плоскость Р.
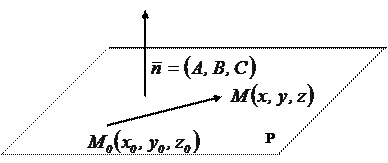
Этот факт вытекает из следующих рассуждений.
Для произвольной точки 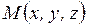 , принадлежащей плоскости, составим вектор
, принадлежащей плоскости, составим вектор 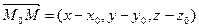 . Т.к. вектор
. Т.к. вектор 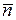 - вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору
- вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору 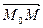 . Тогда скалярное произведение
. Тогда скалярное произведение
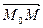 ×
× 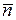 = 0
= 0
Согласно условию ортогональности векторов, получаем уравнение плоскости
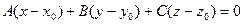 .
.
Например: 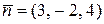 ,
, 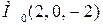 . Тогда уравнение плоскости имеет вид:
. Тогда уравнение плоскости имеет вид: 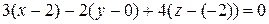 . Раскроем скобки и приведем подобные.
. Раскроем скобки и приведем подобные. 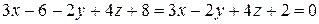 .
.
Чтобы узнать, принадлежит ли точка М(х,у,z) плоскостиР, необходимо подставить ее координаты в уравнение плоскости и убедится, что получилось истинное равенство.
Например: Плоскость Р задана своим общим уравнением.
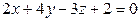 .Проверить, будут ли принадлежать плоскости Р точки
.Проверить, будут ли принадлежать плоскости Р точки 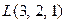 и
и 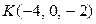 .
.
Подставим в заданное уравнение координаты точки L.
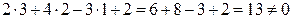 , следовательно
, следовательно 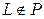 .
.
Подставим в заданное уравнение координаты точки K.
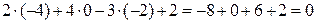 , следовательно
, следовательно 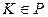 .
.
