Моделирование в процессе решения задач

Моделирование - один из математических методов познания окружающей действительности, при котором строятся и исследуют­ся модели. Моделирование упрощает процесс познания, так как вы­деляет и отображает только нужную грань реальности, абстрагиру­ясь от незначимых факторов.

Текстовая задача — это словесная модель некоторой реальной ситуации. Чтобы решить задачу, надо построить ее математическую модель.

Математическая модель — это описание реального процесса на математическом языке.

Моделирование в процессе решения задач

Математической моделью текстовой задачи является числовое выражение (или несколько числовых выражений, если задача реша­ется по действиям) и уравнение (либо система уравнений).

Этапы моделирования в процессе решения текстовой задачи.

I этап — перевод задачи на математический язык,

II этап - внутримодельное решение.

III этап - перевод полученного решения на естественный язык. На первом этапе происходит переход от одной модели к другой: от словесной модели (текстовой задачи) к вспомогательным моде­лям (рисункам, кратким записям, таблицам и др.), а от них к мате­матической модели задачи (числовым выражениям и уравнениям). На втором этапе находятся значения числовых выражений, решают­ся уравнения. На третьем этапе происходит интерпретация резуль­татов, используя полученное решение, формулируется ответ на воп­рос, поставленный в задаче.

Задание 78

Решите задачу. Выделите этапы моделирования в процессе ее ре­шения.

«Сколько надо купить линолеума, чтобы застелить полы в комнате шириной 3 м и длиной 6 м?»

В процессе развития мышление ребенка переходит от нагляд­но-действенного к наглядно-образному, а впоследствии — к словес­но-логическому. Применение наглядности на любом уровне мыш­ления помогает детям в восприятии и осмыслении задачи, в поиске решения и формулировке ответа. Наглядность может быть непосредственно демонстрирующая задачу — применение конкрет­ных предметов, о которых говорится в задаче. Реальные предметы можно заменить моделями, рисунками, схемами, знаками. Модели­рование в процессе решения задачи развивает образное мышление и учит логически рассуждать.

В зависимости от используемых средств модели можно разделить на схематизированные и знаковые.

К схематизированным моделям относятся:

— вещественные (обеспечивающие физическое действие с предметами, описанными в задаче, или их заместителями, например счетными палочками),

— графические (рисунки, условные рисунки, чертежи, схемы). К знаковым моделям относятся:

Решение задач является одним из средств развития у детей ло­гического мышления, смекалки, сообразительности. В работе с за­дачами совершенствуется умение проводить анализ и синтез, обоб­щать и конкретизировать, выделять главное, отбрасывать несущес­твенное.

Задание 79

1. Для решения предложенной задачи постройте все виды схема­тизированных моделей:

«В коробке 12 карандашей. Скольким детям можно поровну раз­делить все карандаши?»

2. Продемонстрируйте использование различных моделей для ре­шения данной задачи:

«У Пети с Машей всего 15 фломастеров, причем у Маши на 3 фло­мастера больше, чем у Пети. Сколько фломастеров у каждого ре­бенка?»

Вопросы для самоконтроля к теме № 6

1. Какая задача называется текстовой?

2. Какова структура текстовой задачи? З.Что значит решить задачу?

4. Что значит задача решена практическим методом?

5. Что значит задача решена арифметическим методом?

6. Что значит задача решена алгебраическим методом?

7. Что значит задача решена геометрическим методом?

8. Что значит задача решена логическим методом?

9. Назовите основные этапы решения текстовой задачи, раскройте цели и приемы их выполнения.

10. Что такое математическая модель?

11. Назовите этапы моделирования в процессе решения текстовых за­дач.

12. Какие виды моделей используют в процессе решения текстовых задач?

Задания для самостоятельной работы к теме №6

1. Придумайте простую задачу и решите ее различными возможны­ми методами.

2. Придумайте составную задачу и решите ее арифметическим мето­дом двумя способами.

3.Напишите диалог с ребенком (возраст определите сами), отража­ющий процесс решений конкретной задачи по этапам.

4.Придумайте педагогическую ситуацию, в которой ребенок непра­вильно решил задачу, и продемонстрируйте различные способы про­верки правильности ответа.

5.Придумайте задачу, постройте для ее решения различные модели: вспомогательные (реальные предметы, предметы-заместители, рису­нок, схему, чертеж, краткую запись, таблицу) и решающие (число­вое выражение, уравнение).

6.Подберите логические задачи для дошкольников и младших школь­ников и проведите рассуждения в процессе их решения. 7. Предложите бытовую ситуацию (ремонт квартиры, приготовление пищи или др.), в которой вы вынуждены прибегнуть к решению зада­чи. Выявите этапы моделирования в процессе решения этой задачи. 9-7975

ПРИЛОЖЕНИЕ №1Государственный образовательный стандарт по предмету Математика (цикл «Математические и общие естественнонаучные дисциплины») для специальностей: 050704 («Дошкольное образование»), 050705 («Специальное дошкольное образование»),050718 («Специальная педагогика в специальных (коррекционных)

образовательных учреждениях») ЕН.01.

Роль математики в жизни общества; математические понятия, предло­жения, доказательства; элементы теории множеств; понятие величины и ее измерения; история создания систем единиц величин; этапы развития поня­тий натурального числа и нуля; системы счисления; понятие текстовой задачи и процесса ее решения; из истории развития геометрии; основные свойства геометрических фигур на плоскости и в пространстве.

ПРИЛОЖЕНИЕ №2

ВАРИАНТ РАБОЧЕЙ ПРОГРАММЫ ПО МАТЕМАТИКЕ

для специальностей 050704, 050705, 050718

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Курс математики представляет собой дисциплину цикла «Математичес­кие и общие естественнонаучные дисциплины» (ЕН.01.), изучающуюся на базе знаний средней школы в педагогических колледжах на отделениях «Дошкольное образование» (050704), «Специальное дошкольное образова­ние» (050705), «Специальная педагогика в специальных (коррекционных) об­разовательных учреждениях» (050718).

Основная его цель — повысить общеобразовательный и культурный уро­вень будущих воспитателей, дать возможность осуществлять принцип на­учности в работе по математическому развитию детей.

Задачи курса:

1. Выявить место математики среди других наук и ее использование в различных сферах жизни.

2.Расширить знания научных основ предмета (элементы логики, теории множеств, чисел, величин, элементы геометрии).

3.Создать необходимую базу для изучения курсов «Методика матема­тического развития» (специальности 05070Л, 050705), «Методика организа­ции самоподготовки школьников по математике» (специальность 050718) и профессиональной деятельности (развития, воспитания и образования де­тей).

Для целенаправленной и плодотворной работы воспитателю общеобра­зовательных и специальных учреждений необходимо знать суть математических представлений, которые формируются у детей в дошкольном и школьном возрасте.

В данном курсе уделяется внимание вопросам логики и элементам тео­рии множеств, которые не изучаются в явном виде в средней школе, но яв­ляются не только фундаментом всей математики, но основой математичес­кого развития ребенка и формирования всех видов деятельности. Лекции о геометрических фигурах, величинах, натуральных числах расширяют и сис­тематизируют школьные знания, что обеспечит возможность грамотно осу­ществлять помощь детям в изучении математики. Формирование умения решать задачи - одно из условий успешного обучения в школе. Этой про­блеме посвящена последняя тема, которая раскрывает понятие текстовой задачи и ее решения.

Умение пользоваться математическими методами познания, владение математическим языком, сформированное математических представле­ний, знание основных математических понятий и их взаимосвязей необходи­мо воспитателю для осуществления не только образовательных, но и обще-развивающих и коррекционных задач в процессе воспитания детей.

Для усвоения данного содержания возможны различные формы работы со студентами: лекции, семинары, практические занятия и самостоятельная работа. Семинары и практические занятия проводится с целью уточнить и систематизировать знания студентов, полученные на лекциях и в процессе самостоятельной работы, сформировать некоторые профессиональные умения. Самостоятельная работа студентов предусматривает изучение лите­ратуры, составление рефератов, подготовку докладов и сообщений.

В течение семестра проводятся письменные и устные тематические за­четы, на основании результатов которых выставляется семестровая отметка. В конце изучения предмета возможно проведение экзамена.

Данная дисциплина преподается на 2-м курсе, на нее отводится пример­но 40 учебных часов, из них 27 - лекционных и 13 - практических. Возмож­на корректировка в соответствии с учебным планом.

В результате изучения курса «Математики» студенты должны

иметь представление:

о роли математики в жизни общества;

о методах математического познания действительности;

об истории развития геометрии;

об истории развития систем единиц величин;

об этапах развития понятия числа;

знать:

объем и содержание изучаемых математических понятий;

виды явных и неявных определений;

структуру определения понятия через род и видовое отличие;

виды математических предложений;

схемы дедуктивных умозаключений;

Способы доказательства высказываний;

способы задания множеств, соответствии между двумя множествами и отношений между элементами одного множества;

виды отношений между множествами, определения подмножества, равных множеств, дополнения подмножества, равномощных и равночислен­ных множеств;

определения пересечения, объединения, разности множеств;

правила правильной классификации множества;

определение взаимно однозначного соответствия между двумя мно­жествами;

свойства отношений между элементами одного множества;

определения и свойства геометрических фигур на плоскости и в про­странстве;

свойства однородных величин;

значение измерения величин;

свойства натурального ряда;

определение счета элементов множества;

теоретико-множественный смысл натурального числа и нуля;

смысл натурального числа как результата измерения величины;

особенности десятичной системы счисления;

структуру текстовой задачи и методы ее решения;

виды моделей, используемых в процессе решения текстовых задач;

уметь:

правильно формулировать определения математических понятий курса;

определять родовидовые отношения между понятиями;

определять значение истинности высказываний;

задавать отношения на множестве с целью его упорядочения или разби­ения на классы,

изображать изучаемые геометрические фигуры;

измерять величины (длину отрезка, площадь фигуры, объем вещества, массу тела);

записывать число в десятичной системе счисления;

моделировать в процессе решения текстовых задач.

ПРИМЕРНЫЙ ТЕМАТИЧЕСКИЙ ПЛАН

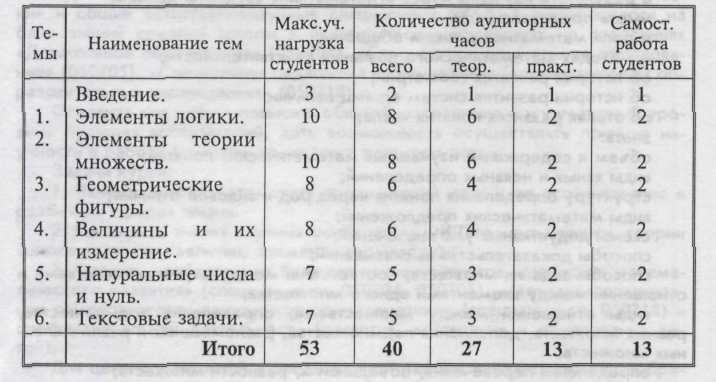
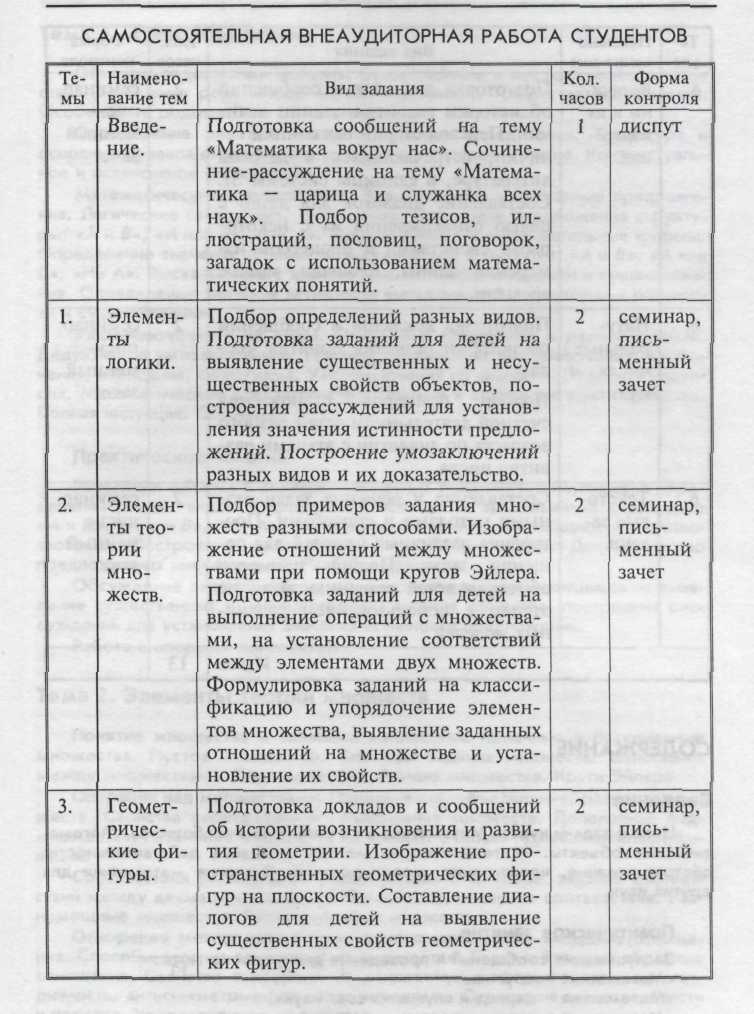
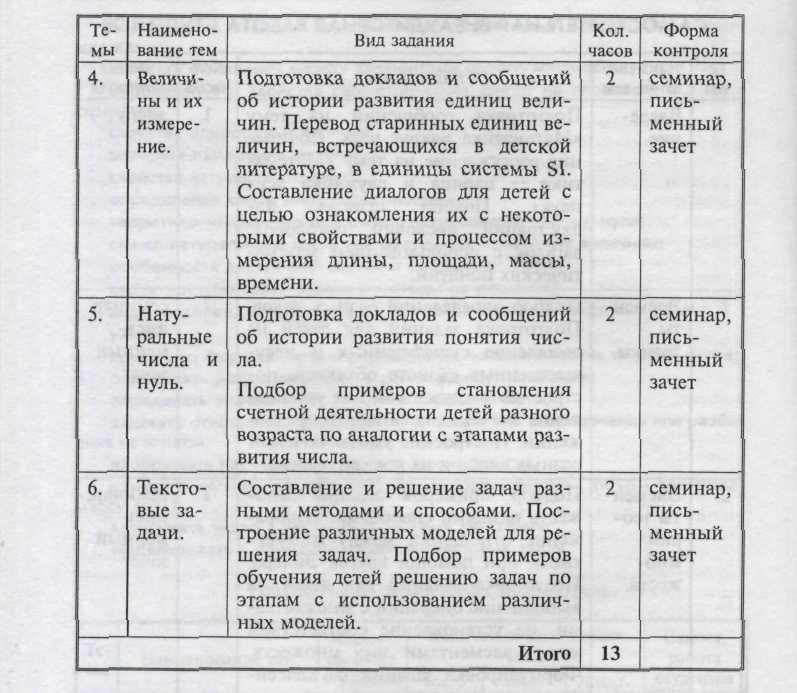
СОДЕРЖАНИЕ

Введение

Цель и задачи курса. Математика и ее роль в жизни общества. Матема­тические объекты. Математические методы познания действительности: абстрагирование, идеализация, моделирование. Значение математики для других наук.

Практическое занятие

Заслушивание сообщений и проведение дискуссии на темы: «Математика вокруг нас»,

«Математика — царица и служанка всея наук», «Математика в устном народном творчестве)! и др.

Тема 1. Элементы логики

Объем и содержание понятия. Существенные и несущественные свой­ства. Отношение рода и вида между понятиями. Тождественные понятия. Особенности родовидовых отношений между понятиями.

Определение понятий. Явные и неявные определения. Структура и основные правила определения через род и видовое отличие. Контекстуаль­ное и остенсивное определения.

Математические предложения. Элементарные и составные предложе­ния. Логические связки: «ив, «или», «не». Составные предложения структу­ры: «А и В», «А или Й», «Не А». Высказывания и высказывательные формы. Определение значения истинности высказываний структуры: «А и В», «А или В», «Не А». Высказывания с кванторами. Кванторы общности и существова­ния. Определение значения истинности высказываний с кванторами общнос­ти и существования.

Умозаключения и их виды. Отношения следования и равносильности. Дедуктивное умозаключение. Правила дедуктивных умозаключений: заклю­чения, отрицания, силлогизма. Умозаключения по аналогии. Неполная индук­ция. Математическое доказательство. Прямые и косвенные доказательства. Полная индукция. Софизмы.

Практическое занятие

Выявление объема и содержания разных понятий. Формулировка опре­делений разных видов. Определение истинности высказываний структуры: «А и В», «А или В», «Не А», высказываний с кванторами общности и сущес­твования. Построение умозаключений различных видов. Доказательство предложенных высказываний. Разбор софизмов.

Обсуждение заданий для дошкольников и младших школьников на выяв­ление существенных и несущественных свойств объектов, построения рас­суждений для установления значения истинности предложений.

Работа с опорным конспектом.