Основные правила комбинаторики

В 1.4.6 мы доказывали теоремы о свойствах конечных множеств. Именно они, лишь в другой формулировке, используются при выводе формул комбинаторики как основные правила.

Правило суммы. Если элемент a может быть выбран m способами, а элемент b другими k способами, то выбор одного из этих элементов – a или b может быть сделан m+k способами.

Пример. На конюшне четыре лошади и два пони. Сколько возможностей выбрать себе скакуна? Здесь используем правило суммы: выбираем один элемент из двух множеств (лошадь или пони) 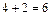способами.

Правило произведения. Если элемент a может быть выбран m способами, а после этого элемент b выбирается k способами, то выбор пары элементов 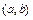в заданном порядке может быть произведен 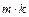способами.

Пример. Пару лыж можно выбрать шестью способами, пару ботинок – тремя. Сколькими способами можно выбрать лыжи с ботинками? Здесь выбираем пару элементов (лыжи, ботинки) – всего 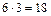способов.

Правило включения-исключения. Если свойством S обладает m элементов, а свойством P обладает k элементов, то свойством S или P обладает 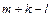элементов, где l – количество элементов, обладающих одновременно и свойством S, и свойством P.

Пример. На полке стоят банки с компотом из яблок и груш. В десяти банках есть яблоки, в шести – груши, в трех – и яблоки, и груши. Сколько всего банок на полке? Здесь 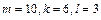, т.е. всего на полке 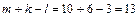банок.

Размещения с повторениями

Задача. Определить количество всех упорядоченных наборов 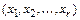длины r, которые можно составить из элементов множества X ( 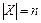), если выбор каждого элемента 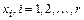, производится из всего множества X.

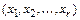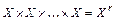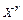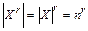Упорядоченный набор – это элемент декартова произведения , состоящего из r одинаковых множителей X. По правилу произведения количество элементов множества равно . Мы вывели формулу .

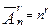Пример. Сколько четырехзначных телефонных номеров можно составить, если использовать все десять цифр?

Здесь 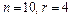, и количество телефонных номеров равно

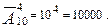
Размещения без повторений

Задача. Сколько упорядоченных наборов 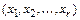можно составить из n элементов множества X, если все элементы набора различны?

Первый элемент 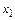можно выбрать n способами. Если первый элемент уже выбран, то второй элемент 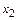можно выбрать лишь 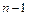способами, а если уже выбран 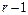элемент 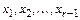, то элемент 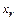можно выбрать 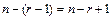способами (повторение уже выбранного элемента не допускается). По правилу произведения получаем

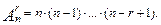
Эта формула записывается иначе с использованием обозначения 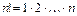. Так как

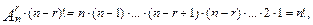
то

.

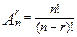Пример. Сколько может быть различных списков победителей олимпиады (первое, второе, третье место), если участвовало 20человек?

Здесь 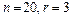, искомым является число

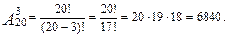
Перестановки без повторений

Рассмотрим частный случай размещения без повторений: если 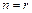, то в размещении участвуют все элементы множества X, т.е. выборки имеют одинаковый состав и отличаются друг от друга только порядком элементов. Такие выборки называются перестановками. Количество перестановок из n элементов обозначают :

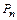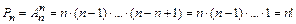
Пример. Сколькими способами можно выстроить очередь в кассу, если хотят получить зарплату шесть человек?

.

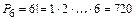Перестановки с повторениями

Пусть множество X состоит из k различных элементов: 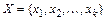. Перестановкой с повторениями состава 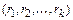будем называть упорядоченный набор длины 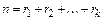, в котором элемент 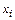встречается 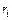раз 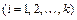. Количество таких перестановок обозначается .

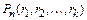Пример. Из букв 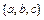запишем перестановку с повторением состава 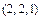. Ее длина 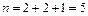, причем буква a входит 2 раза, b – 2 раза, c – один раз. Такой перестановкой будет, например, 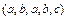или .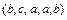

Выведем формулу количества перестановок с повторениями. Занумеруем все одинаковые элементы, входящие в перестановку, различными индексами, т.е. вместо перестановки 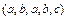получим 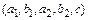. Теперь все элементы перестановки различны, а количество таких перестановок равно 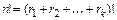. Первый элемент встречается в выборке 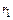раз. Уберем индексы у первого элемента (в нашем примере получим перестановку 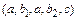), при этом число различных перестановок уменьшится в 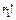раз, т.к. при изменении порядка одинаковых элементов наша выборка не изменится. Уберем индексы у второго элемента – число перестановок уменьшится в 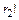раз. И так далее, до элемента с номером k – число перестановок уменьшится в 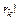раз. Получим формулу

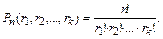
Пример. Сколько различных “слов” можно получить, переставляя буквы слова “передача” ?

В этом слове буквы “е” и “а” встречаются два раза, остальные по одному разу. Речь идет о перестановке с повторением состава 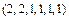длины 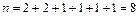. Количество таких перестановок равно

.

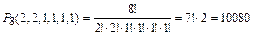Сочетания

Задача. Сколько различных множеств из r элементов можно составить из множества, содержащего n элементов?

Будем составлять вначале упорядоченные наборы по r элементов в каждом. Количество таких наборов (это размещения из n элементов по r) равно 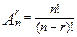. Теперь учитываем, что порядок записи элементов нам безразличен. При этом из 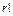различных размещений, отличающихся только порядком элементов, получим одно сочетание. Например, два различных размещения 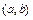и 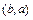из двух элементов соответствуют одному сочетанию 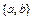. Таким образом, число сочетаний 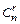в 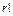раз меньше числа размещений :

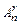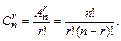
Пример. Количество способов, которыми мы можем выбрать из восьми дворников троих равно

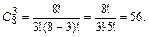
Сочетания с повторениями

Задача. Найти количество 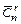сочетаний с повторениями из n предметов по r.

Рассмотрим вывод формулы на примере с фотографиями (см. 2.1.2). Имеется n типов предметов ( 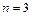негатива). Нужно составить набор из r предметов ( 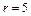фотографий). Наборы различаются своим составом, а не порядком элементов. Например, разными будут наборы состава 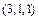и 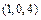– один содержит три фотографии с первого негатива и по одной со второго и с третьего, а другой – одну с первого и четыре с третьего. Разложим эти наборы на столе, разделяя фотографии разного типа карандашами. Карандашей нам понадобится 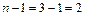, а фотографий 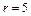. Мы будем получать различные сочетания с повторениями, переставляя между собой эти 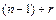предметов, т.е. 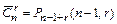- число сочетаний с повторениями из n предметов по r равно числу перестановок с повторениями длины 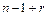состава 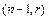. В нашем примере

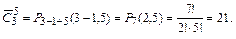
Иначе формулу сочетаний с повторениями можно записать
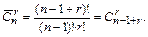
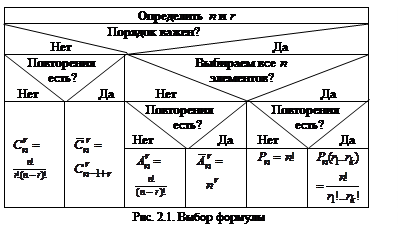