Основные правила комбинаторики

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

ОСНОВНЫЕ ПОНЯТИЯ

Комбинаторика занимается изучением свойств конечных конструкций или объектов, составленных по определенным правилам из элементов счетных множеств. Такие объекты будем называть комбинаторными объектами.

Рассмотрим несколько примеров:

1) последовательности десятичных цифр, образующих правильные записи, представляющие натуральные числа. В этом случае рассматриваемые конструкции собираются в виде записей, составленных из символов десятичных цифр, в которых допускается многократное вхождение одних и тех же символов;

2) правильные записи математических выражений, составленных с помощью математических символов;

3) разнообразные комбинации цветов (букеты) также представляют собой примеры конструкций (заметим, что в данном случае правила составления букетов могут быть достаточно сложными и даже трудно объяснимыми);

4) радиоустройства, конструируемые как соединения различных радиодеталей, также можно рассматривать как комбинаторные объекты;

5) мозаики, составляемые из геометрических фигур заданной формы.

К постановкам задач изучения комбинаторных объектов приводят различные практические потребности в разнообразных областях деятельности.

Например, рассмотрим задачу нахождения вида полинома, получаемого после раскрытия скобок в выражении (x + y)^k.

Понятно, что этот полином представляет собой сумму вида: 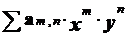Здесь a_m,n - коэффициент при произведении переменных x^myⁿ.

Для нахождения значения произвольного коэффициента a_m,n достаточно определить, сколькими разными способами в последовательности из k перемножаемых выражений (x + y) можно выделить m таких, из которых в составляемое произведение входит x. При этом из остальных m - k выражений x + y произведения (x + y)^k выбирается y.

Рассмотрим еще один пример. Пусть в продаже имеются 15видов игрушечных автомобилей, из которых составляются подарки, содержащие по три разных автомобиля.

Сколько детей может присутствовать на новогоднем празднике так, чтобы каждый ребенок получил подарок, отличный от подарков для других детей.

Нетрудно видеть, что приведенная задача равносильна задаче нахождения числа трехэлементных подмножеств множества, состоящего из 15 элементов.

ВИДЫ КОМБИНАТОРНЫХ ЗАДАЧ

В комбинаторике решаются следующие основные типы задач:

1. Существует ли конструкция, которую можно построить из элементов данного множества по заданным правилам?

2. Как выглядит описание структуры всех комбинаторных объектов, обладающих заданными свойствами?

3. Как построить пример комбинаторного объекта, имеющего заданные свойства?

4. Как построить все комбинаторные объекты с заданными свойствами?

5. Сколько существует различных комбинаторных объектов, обладающих заданными свойствами?

Для получения ответов на перечисленные вопросы используются специфические приемы представления и обработки комбинаторных объектов. Такая специфика определяется тем, что комбинаторные объекты, как правило, являются конечными и могут быть полностью представлены. Конечными или счетными оказываются и конкретные множества таких объектов.

По сравнению с традиционными объектами математики комбинаторные объекты могут иметь более сложную структуру и поэтому оказываются сложными для изучения. Для таких объектов характерно отсутствие непрерывности свойств, проявляющееся в возможности значительного изменения свойств уже при незначительных изменениях в самих объектах.

В настоящем пособии в основном будут рассматриваться задачи, связанные с построением комбинаторных описаний объектов, обладающих заданными свойствами. Кроме того, будет рассмотрена задача определения числа таких объектов. Решение этих задач делает возможным принципиальное решение и других задач. Например, знание структуры описаний объектов из класса, в котором содержатся необходимые объекты, позволяет организовать перебор всех возможных объектов с целью нахождения подходящих. При этом знание количества объектов заданной структуры позволяет оценить возможную продолжительность перебора.

Арифметические выражения и конструкции, позволяющие определять количество комбинаторных объектов с заданными свойствами, называются комбинаторными формулами.

Базис индукции

Для n = 1 правило умножения является справедливым, так как существует ровно m ₁одноэлементных последовательностей, первый элемент которых можно выбрать m₁ разными способами.

Индуктивное предположение

Пусть для n = k количество различных последовательностей, удовлетворяющих условиям правила умножения, равно m₁ m₂ ... m_k.

Индуктивный переход

Пусть n = k + 1. По индуктивному предположению существует ровно m₁m₂ ... m_k различных последовательностей длины k, удовлетворяющих условиям правила умножения, каждая из которых при добавлении еще одного элемента преобразуется в m_k+1 различных последовательностей длины k+1, также удовлетворяющих условиям этого правила. Поэтому общее число последовательностей длины k+1в m_k+1 раз больше числа различных последовательностей, имеющих длину k. То есть всего таких последовательностей ровно m₁ m₂ ... m_k m_k+1.

3. Правило сложения

Пусть заданы непересекающиеся конечные множества A₁, ... , A_k. Тогда мощность объединения этих множеств может быть определена по формуле:

| | = .

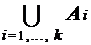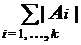Для обоснования справедливости правила сложения заметим, что в значении левой части записи правила каждый элемент объединения непересекающихся множеств A₁, . . . , A_k учтен ровно один раз. Значение в правой части правила учитывает все элементы каждого из множеств A₁, . . . , A_k. Поскольку последние множества непересекающиеся, то всякий элемент их объединения учитывается в правом значении также ровно один раз. Это означает справедливость правила сложения.

Правило умножения - основное для определения количества комбинаторных объектов. К нему сводятся различные вспомогательные комбинаторные соотношения и задачи, преобразуемые в семейства задач, решаемых с помощью этого правила.

Рассмотрим примеры задач, в которых применимо или неприменимо правило умножения.

Пример 1. Определить число различных двоичных наборов длины n, содержащих нечетное число единиц.

Решение

Очевидно, что если n > 1, то первая цифра таких наборов может быть выбрана двумя разными способами. Для всякого i < n - 1 и выбранного начала набора длины i значение следующей цифры набора может быть выбрано двумя способами. Если уже выбраны значения первых n – 1 цифр набора, то значение последней цифры может быть выполнено единственным способом так, чтобы дополнить сумму предшествующих цифр до нечетного значения. Поэтому условия правила умножения выполнены со значениями m₁, . . . , m_n-1, m_n, равными 2, . . . , 2, 1. Следовательно, число двоичных наборов, содержащих нечетное число единиц, равно 2^n-1.

Пример 2. Сколько различных последовательностей десятичных цифр длины 12 можно составить так, чтобы каждая последующая цифра последовательности была не меньше предыдущей.

Решение

Понятно, что первая цифра в таких последовательностях может быть выбрана любой, а число выборов значения каждой последующей цифры в последовательности зависит от предшествующей ей цифры набора. Например, двухэлементная последовательность 2, 3 может быть продолжена 8 способами, а другую двухэлементную последовательность 2, 5 можно продолжить лишь 6 разными способами. Следовательно, для данной задачи условия правила умножения не выполнены. Поэтому для её решения, нельзя использовать правило умножения.

Правило сложения обычно применяется в случаях, когда множество комбинаторных объектов неоднородно, не может быть представлено конструкциями одной и той же структуры, для которой существует простая формула определения числа разных конструкций.

В таких случаях множество всех объектов разбивается на конечное число непересекающихся и более простых классов, в каждом их которых задача подсчета количества объектов может быть решена. Тогда число элементов исходного множества равно сумме мощностей всех непересекающихся классов, на которые было разбито исходное множество.

Рассмотрим пример задачи, решаемой с помощью правила сложения.

Пусть требуется определить число различных слов в английском алфавите, имеющих длину 7 и начинающихся либо с символов WH, либо с символа F. Напомним, что английский алфавит состоит из 26 символов.

Очевидно, что заданное множество слов распадается на две части:

1) множество A₁ - слова, начинающиеся с WH;

2) множество A₂ - слова, начинающиеся с F.

С помощью правила умножения можно показать, что A₁ содержит 26⁵ различных слов, а A₂ - 26⁶ слов. Поэтому общее количество слов в рассматриваемом множестве равно

26⁵ + 26⁶ = 26⁵·27.

РАЗМЕЩЕНИЯ И СОЧЕТАНИЯ

Пусть D - конечное множество, содержащее n элементов.

ОПРЕДЕЛЕНИЕ

Размещениями из n элементов по m элементов множества D называются m-элементные последовательности, каждый член которых является элементом D.

Здесь предполагается, что m ³ 0. При этом, если m = 0, то соответствующее размещение не содержит ни одного элемента и является пустым.

Если множество D неизвестно или не уточняется, то говорят о размещениях из n по m.

Например, слово FALKON может рассматриваться как размещение из 26 элементов символов английского алфавита по 6.

Размещение называется размещением без повторений, если все входящие в него элементы являются разными.

Заметим, что для размещений с повторениями должно выполняться условие m 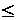n, так как в противном случае по правилу птичьих гнезд в размещении, длина которого больше числа элементов множества, из которого выбираются элементы размещения, будет повторяться хотя бы один символ.

Размещение, в котором могут встречаться одинаковые элементы, называется размещением с повторениями. Из приведенных определений следует, что всякое размещение без повторений одновременно является и размещением с повторениями.

Размещения используются для представления таких комбинаторных объектов, каждому элементу которых должно быть сопоставлено свойство, отличающее его любого из остальных элементов в составе объекта.

Определим число различных размещений из n по m без повторений. В таких размещениях первый элемент может быть выбран n способами, при всяком способе выбора первого элемента выбор второго элемента может быть осуществлен n-1разными способами и т.д. При всяком способе выбора значений первых m -1 элементов последний m-й элемент может быть выбран n - m + 1 способом.

По правилу умножения число таких размещений не зависит от множества A и равно значению произведения:

n ×(n - 1) ×... × (n - m + 1).

Для обозначения число размещений без повторений из n по m применяется специальное выражение 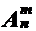. Поэтому: = .

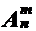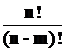В размещениях из n по m с повторениями каждый элемент такого размещения может быть выбран n способами. Поэтому по правилу умножения число размещений с повторениями из n по m равно .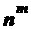

Число размещений с повторениями обозначается как 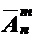. Следовательно, справедливо соотношение: = .

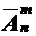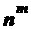Частным случаем размещений без повторений являются размещения всех элементов множества или перестановки элементов множества. Как следует из приведенных формул число P_n перестановок элементов произвольного n элементного множества равно n!

ОПРЕДЕЛЕНИЕ

Сочетанием из n элементов по m элементов n-элементного множества D называется всякая совокупность, состоящая из m элементов D.

Если множество D неизвестно или не уточняется, то говорят о размещениях из n по m.

Так же, как и для размещений, предполагается, что m ³ 0. Если m= 0, то такое сочетание не содержит элементов, т.е. является пустым множеством.

Как следует из приведенного определения в сочетаниях, в отличие от размещений, важен только состав входящих в них элементов, которые в составе сочетания не различаются между собой.

Сочетания могут быть с повторениями и без них.

В сочетании без повторений все элементы совокупности являются разными. Для существования таких сочетаний необходимо выполнение дополнительного условия n ³ m. Всякое такое сочетание может рассматриваться как подмножество того множества, из которого выбираются элементы сочетания. Поэтому множества всех сочетаний без повторений некоторого конечного множества и множество подмножеств этого множества равны.

Из приведенных определений следует, что в сочетании с повторениями могут содержаться одинаковые элементы. Поэтому сочетания без повторений одновременно являются и сочетаниями с повторениями.

Рассмотрим примеры сочетаний

Если покупатель оплачивает сделанную в магазине покупку, то совокупность передаваемых кассиру денег может рассматриваться как:

a) сочетание без повторений, если оплата осуществляется только банкнотами, каждая из которых имеет уникальный номер;

b) сочетание с повторениями, если оплата осуществляется монетами, среди которых могут встречаться неотличимые монеты одного достоинства.

Выведем формулы для определения числа сочетаний из n по m с повторениями и без повторений.

1.Число сочетаний без повторений из nпо m.

Пусть D это некоторое множество, состоящее из n элементов. Рассмотрим все размещения без повторений из n по m, составленные из элементов этого множества. Число таких размещений равно .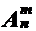

Компоненты каждого такого размещения определяют некоторое сочетание без повторений из n по m, составленное из элементов этого размещения. При этом размещения, отличающиеся лишь порядком вхождения значений, образуют одно и то же сочетание.

Поскольку размещения, соответствующие одному и тому же сочетанию являются перестановками элементов этого сочетания, то всякое сочетание порождается m! различными размещениями. Обозначим число сочетаний из n по m без повторений как .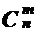

Поэтому имеет место равенство 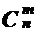m! = .

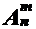Следовательно, справедлива следующая формула для числа сочетаний без повторений: = .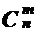

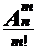Пусть D - это произвольное множество, содержащее n элементов. Тогда число m-элементных подмножеств этого множества равно 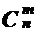. Значит число всех различных подмножеств данного множества равно + + ... + .

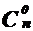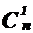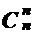С другой стороны, поскольку число подмножеств n-элементного множества равно 2ⁿ, то для сочетаний без повторений справедливо равенство:

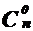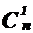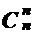+ + ... + = 2ⁿ.

Упражнение

Используя комбинаторные доводы доказать справедливость равенств:

1) (1 - x)^r = 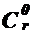x⁰ + ... + (-1)ⁱ 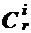xⁱ+ ... + (-1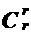)^r x^r.

2) = .

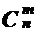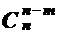2. Число сочетаний с повторениями из nпо m.

Пусть D = {a₁, ... , a_n} - некоторое множество. Сочетания с повторениями, содержащие по m элементов этого множества, будем представлять двоичными последовательностями длины n + m - 1, составленными из m нулей и n - 1 единиц.

Двоичная последовательность, сопоставляемая отдельному сочетанию, состоит из n групп последовательно идущих нулей разделенных, n - 1 единицами.

В i-й группе нулей, отсчитываемой слева направо, столько нулей, сколько экземпляров элемента a_i входит в выбранное сочетание. Если некоторый элемент не входит в сочетание без повторений ни одного раза, то соответствующая ему группа нулей окажется пустой.

Например, если A = {a₁, a₂, a₃, a₄}, то сочетание с повторениями, содержащее 2 элемента a₁, 3 элемента a₂и 2 элемента a₄ представляется двоичным набором:

(0 0 1 0 0 0 1 1 0 0).

Покажем, что определенное ранее соотношение между сочетаниями с повторениями из n по m и двоичными последовательностями длины n + m - 1, содержащими по m нулей, является биективным.

Всякая двоичная последовательность длины n + m - 1, содержащая m нулей, разбивается входящими в неё единицами на n последовательно идущих групп нулей, определяющих количества вхождений элементов a₁, ... , a_n в m элементное сочетание с повторениями. Следовательно, соотношение сочетаний с повторениями и двоичных последовательностей является сюрьективным.

Покажем, что если a = s₁, . . . , s_m+n-1 и b = d₁, . . . , d_m+n-1 - две разные двоичные последовательности, то они представляют разные сочетания с повторениями. Пусть V₁, . . . , V_n и W₁, . . . , W_n - последовательности групп нулей разделенных единицами в последовательностях a и b. Тогда найдется такое i, что V_i ¹ W_i. В противном случае a и b оказываются равными. Следовательно, соотношение сочетаний с повторениями и двоичных последовательностей является инъективным.

Поэтому, число сочетаний с повторениями из n по m равно числу рассматриваемых двоичных последовательностей.

Легко проверить, что последних ровно столько, сколько имеется различных способов выбора из n + m - 1 позиций в двоичных последовательностях, таких n - 1 позиций, в которые записываются единицы. В каждом случае остальные позиции последовательности заполняются нулями.

Число способов выбора различных n - 1 позиций, если имеется n + m -1 разных позиций, равно: .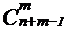

Для обозначения числа сочетаний с повторениями из n по m применяется запись 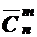. Поэтому справедлива формула:

= _.

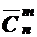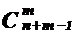Рассмотрим несколько примеров задач, приводящих к использованию сочетаний с повторениями.

1. Определить число способов составления букета из 7 гвоздик, если имеются гвоздики трех цветов.

Очевидно, что букеты как комбинаторные объекты представляют собой сочетания с повторениями из 3 по 7. Поэтому число различных букетов равно .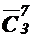

2. Пусть имеется n одинаковых книг. Сколько может быть способов расстановки таких книг на шести полках книжного шкафа?

Очевидно, что всякая расстановка книг на полках соответствует сочетанию с повторениями из 6 элементов по n. В таком сочетании содержатся номера полок. Число вхождений номера некоторой полки в сочетание равно количеству книг, помещенных на эту полку.

Поэтому число указанных расстановок книг на полках равно .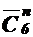

РАЗБИЕНИЯ МНОЖЕСТВ НА ЧАСТИ

Пусть задано множество S = {a₁, ... , a_n}. Требуется распределить элементы S по k именованным множествам S₁, ... , S_kтак чтобы в S₁ попало n₁ элементов, в S₂ - n₂ элементов, . . . , в S_k - n_k элементов множества S. При этом всякий элемент множества S попадает лишь в одно из множеств S₁, ... , S_k.

Поэтому справедливы соотношения:

S = 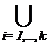S_i и n = 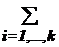|S_i |.

Такое распределение элементов S среди множеств S₁, ... , S_k называется разбиением S на части, имеющие заданные мощности. При этом множества, на которые разбивается S, являются именованными, то есть различаются не только по составу, но и по именам. Поэтому в задаче разбиения S на части важно не только выделение систем подмножеств с заданными мощностями, на которые распадается исходное множество, но и то какие множества образуют какие части.

Рассмотрим несколько примеров задач, приводящих к разбиениям множеств на части.

1. Имеется 15 разных картин, которые требуется разместить в трех залах музея так, чтобы в первом зале было выставлено 6 картин, во втором - 5 картин, в третьем - 4 картины.

Всякое распределение картин по залам, с выполнением сформулированных условий, является разбиением множества из 15 картин на три части, мощности которых равны соответственно 6, 5, 4.

2. Требуется распределить 20заданий поровну между пятью служащими.

Любое распределение заданий представляет собой разбиение множества всех заданий на 5 подмножеств, каждое из которых содержит четыре элемента.

Выведем формулу для нахождения числа различных разбиений конечного множества на части.

Пусть задано множество S = {a₁, ... , a_n}, которое требуется разбить на k подмножеств S₁, ... , S_k, содержащих соответственно по n₁, . . . , n_k элементов.

Возьмем произвольную перестановку a_i1, . . . , a_in элементов S. Для этой перестановки определим разбиение S на части, полагая, что первые n₁ элементов в ней образуют множество S₁, следующие за ними n₂ элементов перестановки образуют S₂ и т.д. Последние n_k элементов перестановки образуют множество S_k. Приведённое правило определяет отображение множества перестановок элементов S во множество разбиений S на части.

Определим свойства этого отображения.

Пусть множества S₁, ... , S_k образуют разбиение S на части с заданными количествами элементов в них. Тогда всякое размещение без повторений всех элементов S, получаемое выписыванием без повторений сначала всех элементов S₁, затем всех элементов S₂ и т.д., пока не будут выписаны без повторений все элементы множества S_k, образует перестановку элементов S. Такая перестановка отображается в исходное разбиение S₁, ... , S_k. Поэтому отображение перестановок множества S в разбиения S является сюрьективным.

Число перестановок, порождающих одно и то же разбиение множества S на части равно количеству последовательностей, составленных из перестановок элементов множеств S₁, ... , S_k, то есть определяется выражением: n₁!... n_k!.

Поскольку всего существует n! перестановок элементов A, и каждому разбиению S соответствует n₁!... n_k! таких перестановок то число различных разбиений S на части S₁, . . . , S_k равно

.

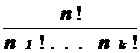Применение последней формулы к приведенному ранее примеру задачи на распределение картин по трем залам музея позволяет утверждать, что существует ровно 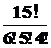вариантов такого распределения.

Упражнения

1.Покажите, используя только комбинаторные доводы (т.е. не прибегая к арифметическим преобразованиям), что число разбиений множества мощности n, на именованные подмножества, имеющие мощности n₁, ... , n_k, равно:

... .

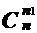
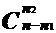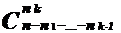2. Сколько существует разбиений множества S = {a₁, ... , a_n} на части S₁, . . . , S_k, имеющие произвольные, в том числе равные нулю, мощности.

3. Сколько имеется способов разбиения n-элементного множества на неименованные части, содержащие n₁, . . . , n_k элементов.

Введенные в рассмотрение комбинаторные конструкции размещений, перестановок, сочетаний и разбиений позволяют решать несложные комбинаторные задачи на представление структуры комбинаторных объектов, составляющих заданные множества, а также определять число элементов в этих множествах.

Процесс решения таких задач состоит в том, чтобы представить элементы множеств в виде конструкций, составленных с помощью размещений, сочетаний или разбиений. При построении таких конструкций может потребоваться использование правил сложения и умножения. Для этого строится подходящее разбиение исходного множества на более однородные классы элементов. При необходимости некоторые классы могут быть дополнительно разбиты на подклассы. Процесс разбиения на подклассы продолжается до получения классов, элементы которых могут быть подсчитаны с помощью уже известных комбинаторных конструкций и соотношений для них. Для множеств, элементы которых значительно различаются между собой по структуре, возможна ситуация, когда разбиение на классы приводит к системе одноэлементных или близких к ним множеств.

В качестве примера рассмотрим следующую задачу.

Сколькими способами можно распределить 10различных предметов среди трех человек, которых обозначим как a, b и c, так чтобы каждому досталось не менее двух предметов.

Понятно, что формула числа разбиений на части для решения этой задачи непосредственно не применима, поскольку мощности множеств предметов, назначаемых a, b и c, на которые разбиваются 10 предметов, не имеют фиксированные мощности и могут изменяться.

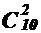
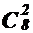
Кажется правдоподобным, что решение рассматриваемой задачи можно получить через рассмотрение таких распределений предметов, при котором сначала a, b и cполучают по два предмета, а после этого между ними произвольным образом распределяются оставшиеся 4 предмета. Число вариантов выполнения первого действия равно 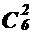. Количество способов выполнения второго действия, для каждого способа выполнения первого действия представляется четырёхэлементным размещением с повторениями из элементов множества {a, b, c}. В этом размещении на первом, втором, третьем, четвертом месте указан человек, который получает соответственно первый, второй, третий и четвёртый предмет из, числа предметов нераспределенных после первого действия. Следовательно, второе действие можно выполнить 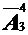= 4³ разными способами. 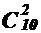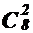Тогда предполагаемый ответ представляет собой произведение чисел 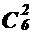и 4³.

Однако нетрудно убедиться в том, что если один человек получает 4 предмета, а два других человека - по 3 предмета, то одни и те же предметы могут назначаться первому человеку несколькими разными способами при выполнении приведенной выше последовательности из первого и второго действия.

Поэтому разные способы выполнения указанного распределения предметов приводят к одному и тому же распределению предметов между a, b и c. Как следствие, число таких распределений не равно числу последовательностей из двух действий, определяемых по правилу умножения как произведение числа вариантов выполнения первого шага на число вариантов выполнения второго шага.

Будем решать рассматриваемую задачу через разложение множества всех распределений предметов среди трёх человек на непересекающиеся случаи, каждый из которых определяется своим набором значений числа предметов, достающихся a, b и c.

Для этого построим все различные разбиения числа 10 на три слагаемых, каждое из которых не меньше, чем 2. Число 10 не велико. Поэтому все варианты можно перебрать, выписывая тройки чисел, суммы которых равны 10, в порядке убывания значений элементов в них. Тогда множество всех наборов из трех чисел, суммы которых равны 10, для которых не уточняются количества предметов каждого конкретного человека, имеет вид:

{(6, 2, 2), (5, 3, 2), (4, 4, 2), (4, 3, 3)}.

Рассмотрим последовательно все 4 случая.

1. Для набора (6, 2, 2) имеется ровно 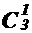способов назначения чисел набора в качестве числа предметов, получаемых a, b и c. (Это следует из того, что достаточно выбрать одного из 3 лиц, который получит 6 предметов.)

После этого для каждого способа такого назначения чисел 6, 2 и 2между a, b и cсуществует ровно 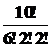способов разбиения множества предметов на 3 именованных подмножества, содержащих соответственно 6, 2и 2 элементов.

По правилу умножения число вариантов распределения предметов в рассматриваемом случае равно: .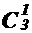

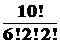2. Для набора (5, 3, 2) существует 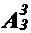способов назначения чисел этого набора в качестве количеств предметов, получаемых a, b и c.

Для каждого способа такого назначения существует 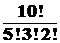способов разделения множества предметов между тремя лицами.

Поэтому число вариантов разбиения множества предметов во втором случае равно .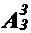

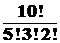3. Для набора (4, 4, 2) окончательное число вариантов равно:

.

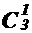
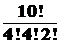4. Для набора (4, 3, 3) окончательное число вариантов равно:

.

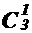
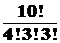На основании правила сложения, суммируя число вариантов в каждом из перечисленных случаев, получим, что искомое число распределений предметов равно:

+ + + .

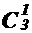
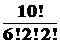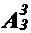
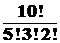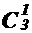
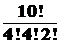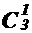
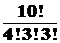ТЕОРЕМА 2.1

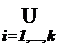| A_i | = n₁ + ... + (-1)^i-1n_i + ... + (-1)^k-1<