Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида:
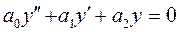 ,
,
где 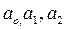 - постоянные коэффициенты,
- постоянные коэффициенты, 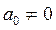
Метод решения. Составляют характеристическое уравнение
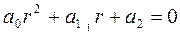 , которое получается из дифференциального уравнения заменой в нем производных искомой функции y соответствующими степенями r, причем сама функция у заменяется единицей.
, которое получается из дифференциального уравнения заменой в нем производных искомой функции y соответствующими степенями r, причем сама функция у заменяется единицей.
Тогда общее решение дифференциального уравнения составляется в зависимости от дискриминанта D характеристического уравнения.
Рассмотрим следующие случаи:
а) D>0; два различных действительных корня 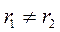 ; тогда
; тогда 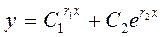 - общее решение дифференциального уравнения;
- общее решение дифференциального уравнения;
б) D=0; два равных действительных корня 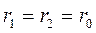 ; тогда
; тогда 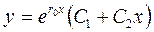 - общее решение дифференциального уравнения;
- общее решение дифференциального уравнения;
в) D<0; два различных комплексных корня: 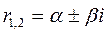 , где
, где 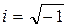 ,
,
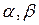 - действительные числа, причем
- действительные числа, причем 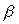 >0.
>0.
Тогда 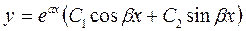 - общее решение дифференциального уравнения.
- общее решение дифференциального уравнения.
Задача. Найти частное решение уравнения 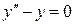 , удовлетворяющее начальным условиям у(0)=0,
, удовлетворяющее начальным условиям у(0)=0, 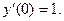
Данная задача с начальными условиями носит название задачи Коши. Составим характеристическое уравнение: r2-1=0. Его решениями являются 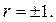 Общее решение уравнения в этом случае (Д>0) находится по формуле
Общее решение уравнения в этом случае (Д>0) находится по формуле 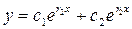 , т.е.
, т.е. 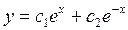 - общее решение.
- общее решение.
Найдем 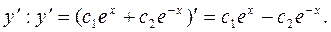
Подставим в уравнения начальные условия:
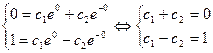
Решая эту систему, получаем 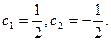 Найденные значения постоянных с1 и с2 подставляем в общее решение и получаем искомое решение
Найденные значения постоянных с1 и с2 подставляем в общее решение и получаем искомое решение 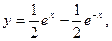 или
или 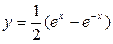
Задача. Найти α и β, если корни уравнения имеют вид:
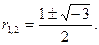
Решение: Преобразуем выражения для 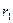 и
и 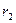 :
:
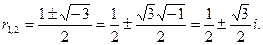
Нетрудно видеть, что 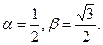
В частном случае, если 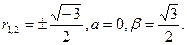
Вопросы для самопроверки:
1.Какое уравнение называется дифференциальным?
2.Что такое порядок дифференциального уравнения?
3.Что называется решением дифференциального уравнения?
4.Сформулируйте задачу Коши.
5.Классификация дифференциальных уравнений. Методы их решений
III. Задачи для контрольной работы
Задание 1. Найти предел:
1.а) 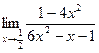 б)
б) 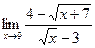 ;
;
в) 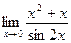 , г)
, г) 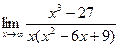 .
.
2. а) 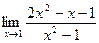 ; б)
; б) 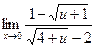 ;
;
в) 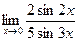 ; г)
; г) 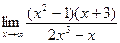 .
.
3. а) 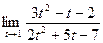 ; б)
; б) 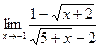 ;
;
в) 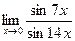 ; г)
; г) 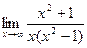 .
.
4. а) 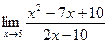 ; б)
; б) 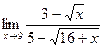 ;
;
в) 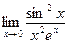 ; г)
; г) 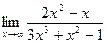 .
.
5. а) 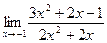 ; б)
; б) 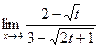 ;
;
в) 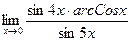 ; г)
; г) 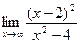 .
.
6. а) 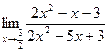 ; б)
; б) 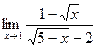 ;
;
в) 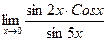 ; г)
; г) 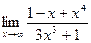 .
.
7. а) 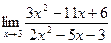 ; б)
; б) 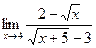 ;
;
в) 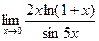 ; г)
; г) 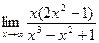 .
.
8. а) 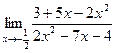 ; б)
; б) 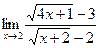 ;
;
в) 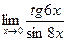 ; г)
; г) 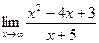 .
.
9. а) 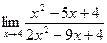 ; б)
; б) 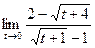 ;
;
в) 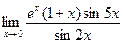 ; г)
; г) 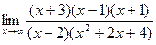 .
.
10. а) 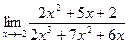 ; б)
; б) 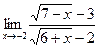 ;
;
в) 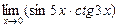 ; г)
; г) 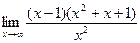 .
.
Задание 2. Найти производную и дифференциал функций:
11. 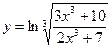 ; 16.
; 16. 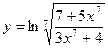 ;
;
12. 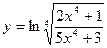 ; 17.
; 17. 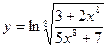 ;
;
13. 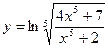 ; ё18.
; ё18. 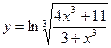 ;
;
14. 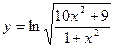 ; 19.
; 19. 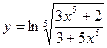 ;
;
15. 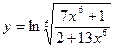 ; 20.
; 20. 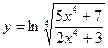 .
.
Найти производную 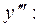
21. 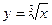 ; 26.
; 26. 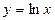 ;
;
22. 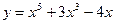 ; 27.
; 27. 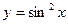 ;
;
23. 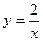 ; 28.
; 28. 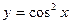 ;
;
24. 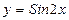 ; 29.
; 29. 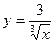 ;
;
25. 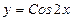 ; 30.
; 30. 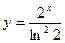 .
.
Найти предел функции с помощью правила Лопиталя:
31. 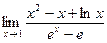 ; 36.
; 36. 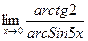 ;
;
32. 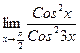 ; 37.
; 37. 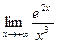 ;
;
33. 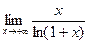 ; 38.
; 38. 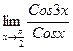 ;
;
34. 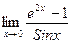 ; 39.
; 39. 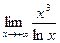 ;
;
35. 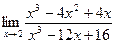 ; 40.
; 40. 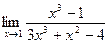 .
.
Исследовать функцию и построить график :
41. 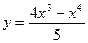 ; 46.
; 46. 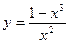 ;
;
42. 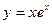 ; 47.
; 47. 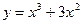 ;
;
43. 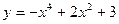 ; 48.
; 48. 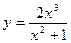 ;
;
44. 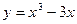 ; 49.
; 49. 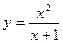 ;
;
45. 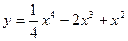 ; 50.
; 50. 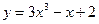 .
.
Задание 3. Найти неопределенный интеграл:
51. а) 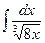 ; б)
; б) 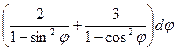 ; в)
; в) 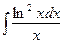 .
.
52. а) 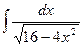 ; б) а)
; б) а) 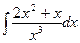 ; в)
; в) 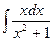 .
.
53. а) 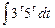 ; б)
; б) 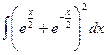 ; в)
; в) 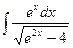 .
.
54. а) 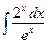 ; б)
; б) 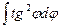 4; в)
4; в) 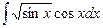 .
.
55. а) 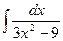 ; б)
; б) 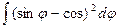 ; в)
; в) 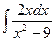 .
.
56. а) 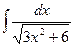 ; б)
; б) 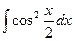 ; в)
; в) 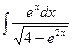 .
.
57. а) 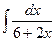 ; б)
; б) 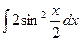 4; в)
4; в) 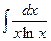 .
.
58. а) 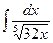 ; б)
; б) 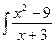 ; в)
; в) 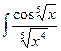 .
.
59. а) 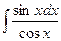 ; б)
; б) 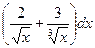 ; в)
; в) 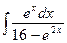 .
.
Вычислить определенный интеграл:
60. а) 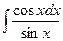 ; б)
; б) 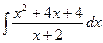 ; в)
; в) 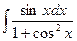 .
.
61. 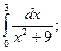 66.
66. 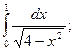
62. 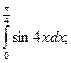 67.
67. 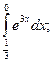
63. 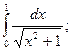 68.
68. 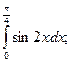
64. 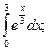 69.
69. 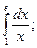
65. 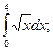 70.
70. 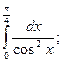
Вычислить площадь фигуры, ограниченной указанными ниже линиями. Сделать чертеж.
71. y = x2, y = x+2; 76. y = x2, y =4x-3;
72. y = x2-3, y = -2x; 77. y = x2-6, y =5x;
73. y = x2-4x, y = -3; 78. y = x2+2x, y 3;
74. y = 2x2-2x-3, y =x2 +3x+3; 79. y = x2-2x-3, y =2x2 –x-5;
75. y = 3x2+2x+1, y =2x2 +3x+3; 80. y = 2x2, y =-x2+3.
Задание 4. Найти частные производные функции Z = Z(x,y)
81. Z = 2x3-3xy2+y5; 86. Z = 4x-7x4y+3y5;
82. Z = x4+2x2-xy3 ; 87. Z = x4+2x2y2+y4;
83. Z = 5x-2x3y2+2y4; 88. Z = x3+3x2y+3xy2+y3;
84. Z = -x2+5xy5-2y3x; 89. Z = 6x3-5x2y3+x3y2;
85. Z = x3-3x2y+xy2-y3; 90. Z = x6+2x3y2+y4.
Найти экстремумы функции:
91. Z = x3+8y3+6xy+5; 96. Z = 3x2-y2+4y+5;
92. Z = x2+xy+y2-3x-6y; 97. Z = x2-4x+y2;
93. Z = x2+y2+8x-2; 98. Z = x2+xy+2y2-x+y;
94. Z = y2+yx+x2-6y-9x; 99. Z = 3x2-6x-y2+4y+8;
95. Z = x2-xy+y2+9x-6y+20; 100. Z = x2+xy+x+2y2+2y.
Задание 5. Решить дифференциальное уравнение:
101. а) 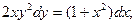 б)
б) 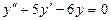 при условиях y(0)=1;
при условиях y(0)=1; 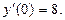
102. а) 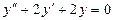 б)
б) 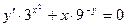 при условии y(0)=1.
при условии y(0)=1.
103. а) 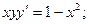 б)
б) 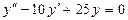 при условиях y(0)=0;
при условиях y(0)=0; 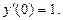
104. а) 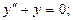 б)
б) 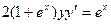 при условии y(0)=0.
при условии y(0)=0.
105. а) 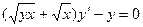 б)
б) 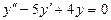 при условиях y(0)=5;
при условиях y(0)=5; 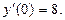
106. а) 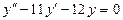 б)
б) 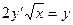 при условии y(4)=1.
при условии y(4)=1.
107. а) 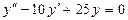 б)
б) 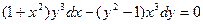 при условии y(1)=-1.
при условии y(1)=-1.
108. а) 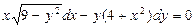 б)
б) 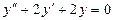 при условиях y(0)=1,
при условиях y(0)=1, 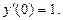
109. а) 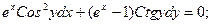 б)
б) 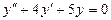 при условиях y(0)=-3,
при условиях y(0)=-3, 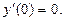
110. а) 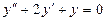 ; б)
; б) 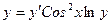 при условиях
при условиях 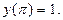
Список литературы
1. Антонов, В.И. Элементарная математика для первокурсника: учеб. пособие для студентов вузов/ В.И. Антонов, Ф.И. Копелевич. - СПб.; М.; Краснодар: Лань, 2013. - 101 с.: граф., рис.. - (Учебники для вузов. Спец. лит.). - Библиогр.: с. 99.
2. Кузнецов, Л.А. Сборник заданий по высшей математике. Типовые расчеты: учеб. пособие для студентов вузов. По напр. подгот. и спец. в области естественных наук и мат., техники и технологий, образования и пед. / Л.А. Кузнецов. - 12-е изд., испр.. - СПб.; М.; Краснодар: Лань, 2013. - 238 с.: табл.. - (Учебники для вузов. Спец. лит.)
3. Назаров, А.И. Курс математики для нематематических специальностей и направлений бакалавриата: учеб / А.И. Назаров, И.А. Назаров. - СПБ: Лань, 2011.- 576 с
.
Содержание
ВВЕДЕНИЕ. 3
I. Содержание дисциплины «Математика». 3
1.1 Дифференциальное исчисление функций одной переменной. 3
1.2 Дифференцирование функций нескольких переменных. 4
1.3 Интегральное исчисление функций одной переменной. 4
1.4 Обыкновенные дифференциальные уравнения. 5
1.5 Элементы теории вероятностей и математической статистики. 5
II. Методические указания по изучению курса дисциплины «Математика». 7
2.1 Дифференциальное исчисление функций одной переменной. 7
2.1.1 Понятие числовой функции. Свойства функции. 7
2.1.2 Предел функции. 11
2.1.3 Производная функции одного переменного. 19
2.1.4 Приложения дифференциального исчисления к исследованию функции 23
2.1.5 Правило Лопиталя. 27
2.2 Дифференциальное исчисление функции двух переменных. 30
2.2.1 Функция двух переменных. 30
2.2.2 Производная сложной функции. 32
2.2.3 Экстремум функции двух переменных. 34
2.3 Интегральное исчисление функции одной переменной. 36
2.3.1 Первообразная. Неопределенный интеграл. 36
2.3.2 Определенный интеграл. 42
2.3.3 Приложения определенного интеграла. 44
2.4 Обыкновенные дифференциальные уравнения. 46
2.4.1 Основные понятия. 46
2.4.2 Дифференциальные уравнения первого порядка с разделяющимися переменными. 48
2.4.3 Простейшие дифференциальные уравнения n – го порядка, допускающие понижение порядка методом интегрирования обеих частей уравнения. 50
2.4.4 Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. 50
III. Задачи для контрольной работы.. 50
Список литературы.. 50
