Физический смысл производной
Введение.
Цель математической подготовки студентов-медиков – это ознакомление их с основными понятиями и методами современного математического аппарата, необходимого для решения задач физического, химического, биологического и другого характера, которые будут встречаться в процессе изучения профилирующих дисциплин, а так же в дальнейшей профессиональной деятельности.
Тематика данного учебного пособия соответствует учебной программе «Математика» для студентов медицинского факультета.
Учебное пособие разработано с учетом прикладного характера изложения основных понятий и методов, а также, недостаточно высокого исходного уровня подготовки студентов по математике.
В данном учебном пособии содержится большое количество конкретных примеров физического, химического и медико-биологического содержания, соответствующих профессиональным потребностям будущих специалистов.
Глава 1.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Функции
Изучая различные процессы и явления – физические, химические, биологические и др. – часто приходиться встречаться с величинами, связанными между собой той или иной зависимостью. Например, путь,, проходимый свободно падающим в пустоте телом, зависит только от времени, давление в паровом котле зависит только от температуры пара, скорость размножения бактерий зависит от условий окружающей среды, которые также могут быть охарактеризованы некоторыми величинами.
Одним из наиболее важнейших видов зависимостей между величинами является функциональная зависимость. Она представляет собой одно из самых важных понятий математики
Функциональная зависимость
Определение. Функцией называется закон или соответствие, по которому каждому значения переменной  ставиться в соответствие единственное значение переменной
ставиться в соответствие единственное значение переменной 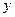 .
.
Переменная  при этом называется аргументом или независимой переменной, а
при этом называется аргументом или независимой переменной, а 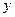 – функцией или зависимой переменной. Относительно самих величин
– функцией или зависимой переменной. Относительно самих величин  и
и 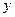 говорят, что они находятся в функциональной зависимости. Аналитически (т. е. с помощью формулы) эту зависимость сокращенно обозначают
говорят, что они находятся в функциональной зависимости. Аналитически (т. е. с помощью формулы) эту зависимость сокращенно обозначают
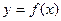 ,
,
где символ 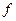 называется характеристикой функции.
называется характеристикой функции.
Если каждому значению переменной  соответствует одно значение
соответствует одно значение 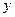 , то функция называется однозначной. Если хотя бы некоторым значениям переменной
, то функция называется однозначной. Если хотя бы некоторым значениям переменной  соответствует несколько значений
соответствует несколько значений 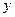 , то функция называется многозначной.
, то функция называется многозначной.
Определение. Совокупность всех значений независимой переменной  , для которых функция
, для которых функция 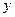 определена, называется областью определения или областью существования функции. Обозначается:
определена, называется областью определения или областью существования функции. Обозначается: 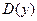 .
.
Определение. Областью значений функции называются все допустимые значения переменной 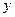 . Обозначается:
. Обозначается: 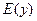 .
.
Определение. Функция 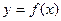 называется возрастающей на интервале
называется возрастающей на интервале 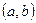 , если для любых двух значений
, если для любых двух значений 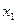 и
и 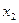 , принадлежащих этому интервалу и удовлетворяющих неравенству
, принадлежащих этому интервалу и удовлетворяющих неравенству 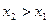 , выполняется неравенство
, выполняется неравенство 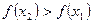 , и убывающей, если при этих же условиях выполняется неравенство
, и убывающей, если при этих же условиях выполняется неравенство 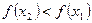 . Иначе, функция называется возрастающей на интервале
. Иначе, функция называется возрастающей на интервале 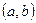 , если на этом интервале большему значению аргумента соответствует большее значение функции, и убывающей в противном случае.
, если на этом интервале большему значению аргумента соответствует большее значение функции, и убывающей в противном случае.
Определение. Если функция во всей области своего определения только возрастает или только убывает, то она называется монотонной.
Определение. Функция 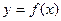 называется четной, если для всех значений
называется четной, если для всех значений  , принадлежащих области определения функции, выполняется равенство
, принадлежащих области определения функции, выполняется равенство 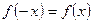 .
.
Определение. Функция 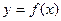 называется нечетной, если для всех значений
называется нечетной, если для всех значений  , если для всех значений
, если для всех значений  , выполняется равенство
, выполняется равенство 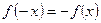 .
.
График четной функции симметричен относительно оси ординат, нечетной – относительно начала координат.
Определение. Функция 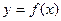 называется периодической с периодом Т, если для всех значений
называется периодической с периодом Т, если для всех значений  , принадлежащих области определения функции, выполняется равенство
, принадлежащих области определения функции, выполняется равенство 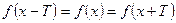 .
.
Определение. Функция 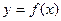 называется ограниченной на отрезке
называется ограниченной на отрезке 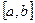 , если существует такое положительное число
, если существует такое положительное число 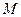 , что для любых значений
, что для любых значений  , принадлежащих этому отрезку, выполняется неравенство
, принадлежащих этому отрезку, выполняется неравенство 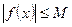 .
.
Функция вида 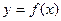 называется явной (заданной в явном виде), а функция
называется явной (заданной в явном виде), а функция 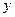 , заданная уравнением
, заданная уравнением 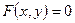 , т. е. уравнением, не разрешенным относительно переменной
, т. е. уравнением, не разрешенным относительно переменной 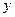 , называется неявной.
, называется неявной.
1.2. Способы задания функций
Задать функцию означает установить правило (закон), с помощью которого по данным значениям независимой переменной следует находить соответствующие им значения функции. Рассмотрим некоторые способы задания функций.
Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
 | -1 | -2 | |||
 |
Например:
Графический способ. Графиком функции 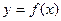 называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом. Например,
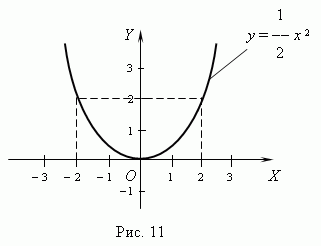
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Например: 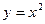 .
.
Этот способ дает возможность по каждому численному значению аргумента  найти соответствующее ему численное значение функции
найти соответствующее ему численное значение функции 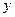 точно или с некоторой точностью.
точно или с некоторой точностью.
Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
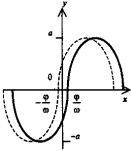
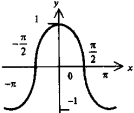
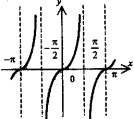
Графики элементарных функцй
|
1.4. Преобразования графиков функций
Иногда бывает важным построить график функции отталкиваясь от графика той или иной элементарной функции с помощью определенных правил преобразования графиков функции или используя правила построения графиков сложных функции.
Приведем некоторые простейшие методы построения графиков функции.
График функции 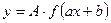 может быть получен из графика функции
может быть получен из графика функции 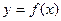 с помощью простых геометрических преобразований. Приведем их в таблице:
с помощью простых геометрических преобразований. Приведем их в таблице:
| y=f(x)+A | Параллельный перенос его вдоль оси OY на А единиц вверх, если А>0 и на |A| единиц вниз, если A<0/ |
| y=f(x-a) | Параллельный перенос его вдоль оси ОY на a единиц вправо, если а>0, и на -а единиц влево, если a<0. |
| y=kf(x), k>0 | Растяжение вдоль оси ОХ в k раз, если k>1, и сжатие в 1/k раз, если 0<k<1. |
| y=f(kx), k>0 | Сжатие вдоль оси ОХ относительно оси OY в k раз, если k>1 и растяжение в 1/k раз, если 0<k<1. |
| y=-f(x) | Симметричное отображение графика относительно оси ОХ. |
| y=|f(x)| | Часть графика функции y=f(x), расположенная ниже оси ОХ, симметрично отражается относительно этой оси, остальная часть графика остается без изменения. |
| y=f(-x) | Симметричное отображение графика относительно оси ОY. |
| Y=f(|x|) | Часть графика функции y=f(x), расположенная в области x ³0, остается без изменения, а его часть для области x £0 заменяется симметричным отображением относительно оси OY. |
Производная функции
Понятие производной – одно из основных понятий математического анализа. Его значимость заключается в том, что производная функции характеризует скорость изменения этой функции при изменении ее аргумента.
Производная функции
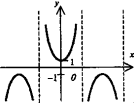
Рассмотрим некоторую непрерывную функцию (т. е. функцию, графически представляемую непрерывной линией), характеризующую зависимость 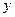 от
от  , причем ее график имеет вид, представленный на рис. 1.
, причем ее график имеет вид, представленный на рис. 1.
|
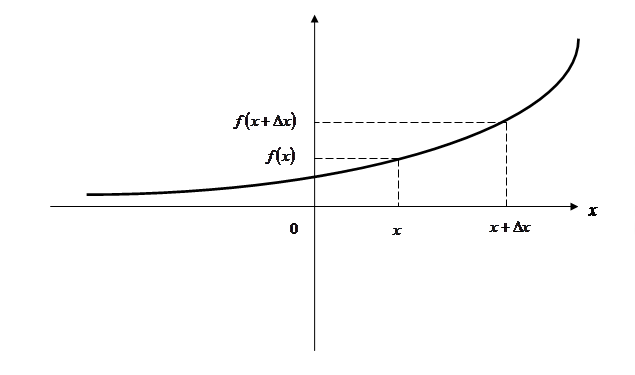
Рис.2.
Когда аргумент функции  получает приращение
получает приращение 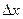 , функция
, функция 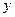 получает приращение
получает приращение 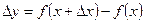 . Значения
. Значения  и
и 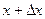 должны принадлежать области определения функции.
должны принадлежать области определения функции.
При уменьшении приращения аргумента 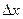 приращение функции
приращение функции 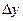 также уменьшается и их отношение
также уменьшается и их отношение 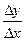 в общем случае претерпевает некоторое изменение.
в общем случае претерпевает некоторое изменение.
Определение. Производной функции 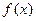 в точке
в точке  называется предел приращения функции
называется предел приращения функции 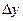 к приращению аргумента
к приращению аргумента 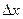 , когда
, когда 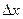 стремиться к нулю
стремиться к нулю 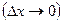 , при условии что этот предел существует.
, при условии что этот предел существует.
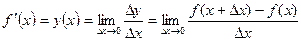 .
.
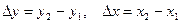 .
.
Процесс нахождения производной называется дифференцированием.
Определение. Функция, для которой в точке  существует конечная производная, называется дифференцируемой в данной точке.
существует конечная производная, называется дифференцируемой в данной точке.
Если функция имеет конечные производные во всех точках некоторого промежутка, то она называется дифференцируемой на данном промежутке.
Существуют следующие обозначения производной: 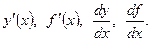
Производная сложной функции
Теорема. Если функция 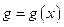 определена и дифференцируема на интервале
определена и дифференцируема на интервале 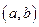 , причем областью ее значений является интервал
, причем областью ее значений является интервал 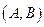 , а функция
, а функция 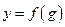 определена и дифференцируема на интервале
определена и дифференцируема на интервале 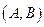 , то производная сложной функции
, то производная сложной функции 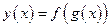 существует и равна произведению производной внешней функции по ее аргументу
существует и равна произведению производной внешней функции по ее аргументу 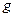 на производную внутренней функции
на производную внутренней функции 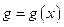 по ее аргументу
по ее аргументу  :
:
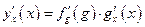 ,
,
Причем в этой формуле при обозначении производных под штрихом в виде индексов указаны переменные, по которым ведется дифференцирование.
Пример.  Найти производную сложной функции
Найти производную сложной функции 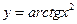 .
.
Т. к. данная функция является сложной, то введем в рассмотрение внутреннюю функцию  и внешнюю функцию
и внешнюю функцию 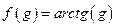 . С учетом этих обозначений исходная функция может быть представлена в виде
. С учетом этих обозначений исходная функция может быть представлена в виде 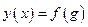 и для нахождения ее производной применяем формулу
и для нахождения ее производной применяем формулу 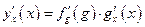 :
:
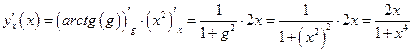
Производные высших порядков
Производную 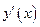 называют еще первой производной, или производной первого порядка, функции в отличие от так называемых производных высших порядков.
называют еще первой производной, или производной первого порядка, функции в отличие от так называемых производных высших порядков.
Производная 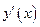 функции
функции 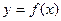 в общем случае представляет собой некоторую новую функцию, которая в свою очередь тоже может быть дифференцируемой. Следовательно, можно найти производную и этой функции, представляющую собой производную от производной исходной функции и называемую второй производной, или производной второго порядка, исходной функции. Производную второго порядка принято обозначать
в общем случае представляет собой некоторую новую функцию, которая в свою очередь тоже может быть дифференцируемой. Следовательно, можно найти производную и этой функции, представляющую собой производную от производной исходной функции и называемую второй производной, или производной второго порядка, исходной функции. Производную второго порядка принято обозначать 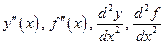 .
.
Производную от производной второго порядка, если она существует, называют третьей производной функции , или производной третьего порядка, и обозначают 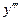 или
или 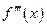 и т. д.
и т. д.
Определение. Производные порядков выше первого называются производными высших порядков.
При этом производная 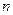 -го порядка определяется как производная от производной предыдущего порядка, т. е.
-го порядка определяется как производная от производной предыдущего порядка, т. е.
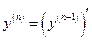 .
.
Пример. Найти вторую производную функции 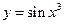 .
.
Найдем сначала первую производную 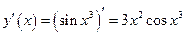 .
.
Найдем вторую производную
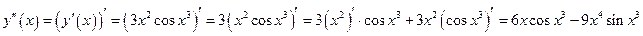
Теорема 1.
1) Если функция 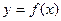 дифференцируема и возрастает на интервале
дифференцируема и возрастает на интервале 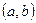 , то производная этой функции не отрицательна
, то производная этой функции не отрицательна 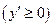 во всех точках данного интервала.
во всех точках данного интервала.
2) Если функция 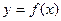 дифференцируема и убывает на интервале
дифференцируема и убывает на интервале 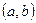 , то производная этой функции не положительна
, то производная этой функции не положительна 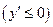 во всех точках данного интервала.
во всех точках данного интервала.
Эту теорему называют теоремой о необходимых признаках возрастания и убывания функции, поскольку в ней указывается, какой должна быть производная дифференцируемой функции на интервале в случаях соответственно возрастания и убывания функции.
Необходимо помнить, что неотрицательность производной является лишь необходимым, но не достаточным условием для утверждения о возрастании функции, точно так же, как неположительность производной не является достаточным условием для утверждения о ее убывании.
Теорема 2.
1) Если производная функции положительна 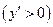 на интервале
на интервале 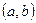 ,то функция возрастает на этом интервале.
,то функция возрастает на этом интервале.
2) Если производная функции отрицательна 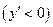 на интервале
на интервале 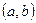 ,то функция убывает на этом интервале.
,то функция убывает на этом интервале.
Эту теорему называют теоремой о достаточных признаках возрастания и убывания функции, поскольку в ней указывается, при каком знаке производной на интервале дифференцируемая функция возрастает и при каком – убывает.
Решение.
1. Найдем область определения функции. Дробь определена, если знаменатель отличен от нуля, т. е.
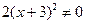 ;
; 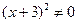 ;
; 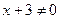 ;
; 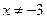 .
.
И так, 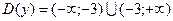 .
.
2. Найдем производную функции
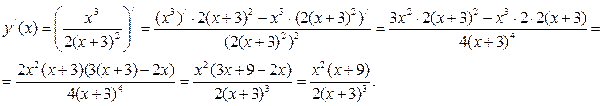
3. Приравняем производную к нулю и решим уравнение 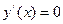 ;
;
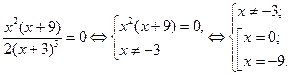
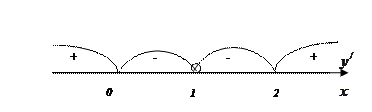
4. Найденные критические точки и точки, в которых производная не существует, отметим на числовой оси в порядке возрастания
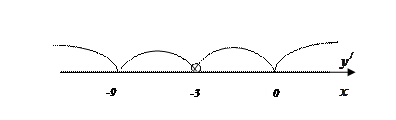
5. Определим знаки производной на интервалах, на которые делят числовую ось критические точки и отметим полученные результаты над соответствующими интервалами;
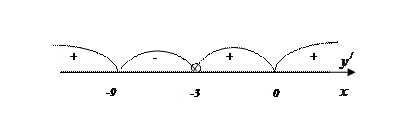
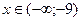
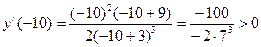 ;
;
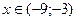
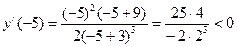 ;
;
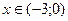
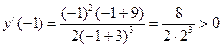 ;
;
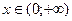
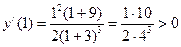 .
.
6. С учетом знака производной находим интервалы возрастания (на них производная положительная) и убывания (на них производная отрицательная). Функция возрастает при 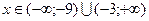 и убывает при
и убывает при 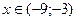 .
.
7. Находим точки экстремумов функции (т. е. точки, при переходе через которые знак производной меняется на противоположный).
Поскольку при переходе через точку 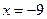 первая производная
первая производная 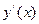 меняет знак с «+» на «-», то это точка максимума:
меняет знак с «+» на «-», то это точка максимума:
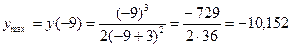 .
.
Итак, 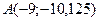 − точка локального максимума.
− точка локального максимума.
Примерная схема построения графика функции
С учетом всего вышеописанного для исследования функции и дальнейшего построения графика следует придерживаться следующей схеме:
1. Область существования функции.
2. Симметрия графика функции (четность, нечетность).
3. Точки пересечения графика функции с осями координат.
4. Использование первой производной: интервалы возрастания и убывания, экстремумы функции.
5. Использование второй производной: участки выпуклости и вогнутости графика, точки перегиба.
6. Составление сводной таблицы результатов исследования.
7. Построение графика.
Пример. Исследовать функцию и построить ее график
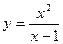
Решение.
1. Найдем область определения функции. Дробь определена, если знаменатель отличен от нуля, т. е.
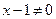 ;
; 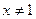 .
.
И так, 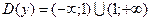 .
.
2. Исследуем функцию на четность. Так как точка 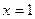 не входит в область определения функции, а точка
не входит в область определения функции, а точка 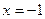 принадлежит области определения функции, т. е. область определения рассматриваемой функции не симметрична относительно начала координат, то функция не является чётной и не является нечётной.
принадлежит области определения функции, т. е. область определения рассматриваемой функции не симметрична относительно начала координат, то функция не является чётной и не является нечётной.
3. Найдём точки пересечения графика функции с осями координат − с осью 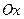 :
:
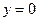 ;
; 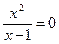 ;
; 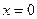 .
.
и осью 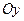 :
: 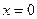 ,
, 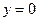 .
.
График функции пересекается с координатными осями в начале координат − точке 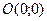 .
.
4. Определим экстремумы и интервалы монотонности функции. Для этого найдём первую производную 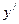 и решим уравнение
и решим уравнение 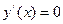 ;
;
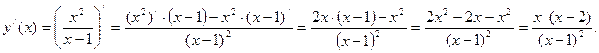
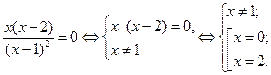
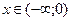
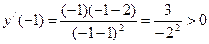 ;
;
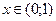
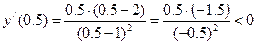 ;
;
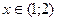
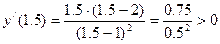 ;
;
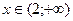
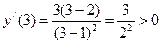 .
.
Функция возрастает при 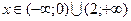 и убывает при
и убывает при 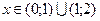 .
.
Поскольку при переходе через точку 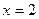 первая производная
первая производная 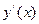 меняет знак с «-» на «+», то это точка минимума:
меняет знак с «-» на «+», то это точка минимума:
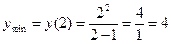 .,
.,
а при переходе через точку 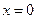 первая производная
первая производная 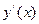 меняет знак с «+» на «-», то это точка максимума:
меняет знак с «+» на «-», то это точка максимума:
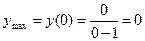
Итак, 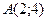 − точка локального минимума,
− точка локального минимума, 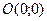 – точка локального максимума.
– точка локального максимума.
5. Найдем интервалы выпуклости и вогнутости графика функции и точки перегиба. Для этого найдём вторую производную 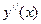 и решим уравнение
и решим уравнение 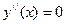 :
:
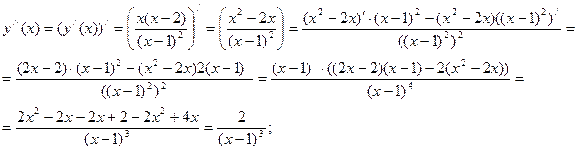
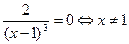
Левая часть данного уравнения в нуль никогда не обращается 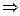 точек перегиба нет.
точек перегиба нет.
Исследуем знак 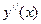 на промежутках
на промежутках 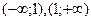 :
:
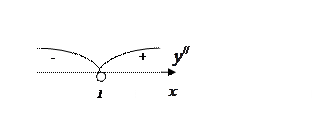
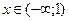
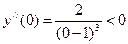 ;
;
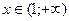
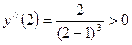 .
.
График функции выпуклый вверх при 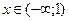 ; вогнутый − при
; вогнутый − при 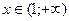 .
.
6. Составим сводную таблицу.
 | 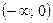 | 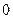 | 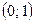 | 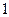 | 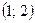 | 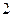 | 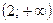 |
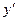 | + | – | Не сущ. | – | + | ||
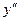 | – | -2 | – | Не сущ. | + | + | |
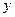 |  |   | Не сущ. | 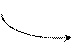 |  | ||
| max | min |
7. Постоим график.
Неопределенный интеграл
Ранее мы рассматривали способы нахождения производных функции, а также их применение к исследованию функций, что составляет основную задачу раздела высшей математики, называемого дифференциальным исчислением. Далее перейдем к рассмотрению основ интегрального исчисления, которое решает обратную задачу, а именно задачу нахождения функции по ее производной или дифференциалу.
Таблица простейших неопределенных интегралов
Учитывая то, что формулы для неопределенных интегралов от некоторых элементарных функций могут быть получены исходя из того, что интегрирование представляет собой операцию обратную дифференцированию, получим следующую таблицу простейших неопределенных интегралов.
1. 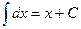 8.
8. 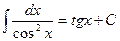
2. 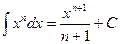 9.
9. 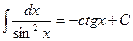
3. 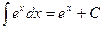 10.
10. 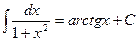
4. 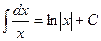 11.
11. 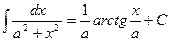
5. 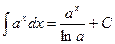 12.
12. 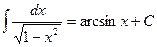
6. 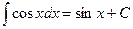 13.
13. 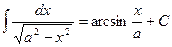
7. 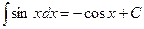 14.
14. 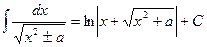
Определенный интеграл
Понятие определенного интеграла используют в ряде практических задач, в частности в задачах по вычислению площадей плоских фигур, объемов тел вращения, расчету работы, производимой переменной силой, ………………………………………………………..и т. д.
Формула Ньютона – Лейбница
Теорема. Значение определенного интеграла равно разности значений любой первообразной от подынтегральной функции, взятой при верхнем и нижнем пределах интегрирования.
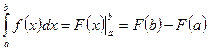

Данная формула называется формулой Ньютона – Лейбница и дает практически удобный метод вычисления определенного интеграла в том случае, когда известна первообразная подынтегральной функции.
Основными методами интегрирования определенного интеграла являются те же, что и для неопределенного.
Пример. Вычислить определенный интеграл
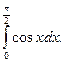
Решение. 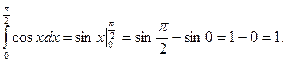
Дифференциальные уравнения
Математическое описание различных процессов и явлений – физических, химических, биологических и т. д. – часто содержит уравнения, в которых присутствуют не только изучаемые величины, но и производные различных порядков от этих величин.
6.1. Основные понятия и определения дифференциальных уравнений
Определение. Дифференциальным уравнением называется уравнение, связывающее независимую переменную, неизвестную функцию и её производные различных порядков.
Дифференциальное уравнение относительно одной независимой переменной называется обыкновенным.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в него.
Например: 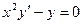 – ДУ 1-го порядка
– ДУ 1-го порядка
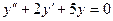 – ДУ 2-го порядка
– ДУ 2-го порядка
Общий вид обыкновенного дифференциального уравнения определяется следующим выражением:
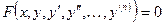 (1)
(1)
Определение. Решением дифференциального уравнения называется такая функция 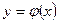 , которая будучи подставленной в уравнение вместе со своими производными, обращает его в тождество (верное равенство).
, которая будучи подставленной в уравнение вместе со своими производными, обращает его в тождество (верное равенство).
График решения дифференциального уравнения называется интегральной кривой.
Определение. Общим решением дифференциального уравнения (1) называется функция вида
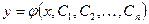 (2)
(2)
Если в (2) постоянным 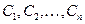 придать конкретные числовые значения, то полученная функция называется частным решением дифференциального уравнения.
придать конкретные числовые значения, то полученная функция называется частным решением дифференциального уравнения.
Задача Коши.
Общий вид дифференциального уравнения первого порядка определяется выражением:
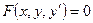 (3)
(3)
Если уравнение (3) разрешимо относительно 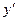 , то уравнение (3) принимает вид:
, то уравнение (3) принимает вид:
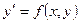 (4)
(4)
Общим решением уравнения (3) или (4) является множество функций вида 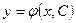 , где
, где 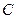 – произвольная постоянная. Придавая различные значения произвольной постоянной
– произвольная постоянная. Придавая различные значения произвольной постоянной 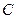 , можно получить частные решения. На плоскости
, можно получить частные решения. На плоскости 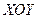 общее решение представляет собой семейство интегральных кривых, соответствующих каждому частному решению.
общее решение представляет собой семейство интегральных кривых, соответствующих каждому частному решению.
Условия вида 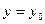 при
при 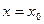 или
или 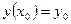 называются начальными условиями.
называются начальными условиями.
Задача нахождения частного решения дифференциального уравнения (3) и (4), удовлетворяющая начальному условию, называется задачей Коши.
Глава 2.
Элементы комбинаторики.
Комбинаторика – это наука о расположении элементов в определенном порядке и о подсчете числа способов такого расположения.
Существуют два основных правила комбинаторики:
1. Правило « суммы»: Если элемент 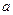 можно выбрать
можно выбрать 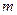 способами, а элемент
способами, а элемент 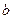 –
– 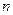 способами, то элемент «либо
способами, то элемент «либо 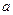 , либо
, либо 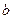 » можно выбр
» можно выбр

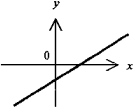
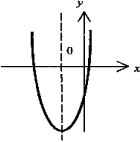
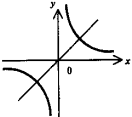
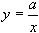 . При а > 0 расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а > 0) или у - - х(а < 0).
. При а > 0 расположена в I и III четвертях, при а < 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х(а > 0) или у - - х(а < 0). 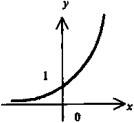
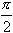 )
) 
 ,
,