Распределения случайных величин

Дискретные и непрерывные случайные величины

Распределения случайных величин

Количественная характеристика опыта состоит в определении значений некоторых величин, полученных в результате опыта.

Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных (причем до опыта невозможно предвидеть – какое именно).

Случайные величины обозначают заглавными буквами Х, Y, Z, …, а их возможные значения – соответствующими строчными буквами x, y, z, ….

Если случайное событие полностью характеризуется вероятностью появления этого события, то описание вероятностных свойств случайных величин является более сложной задачей.

Вероятностные свойства случайных величин описываются законом распределения, т.е. соотношением, устанавливающим связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения полностью характеризует случайную величину.

Различают дискретные и непрерывные случайные величины.

Дискретные случайные величины

5.2.2.1.Понятие дискретной случайной величины

Дискретной случайной величиной называют величину, принимающую различные значения, которые можно записать в виде конечной или бесконечной последовательности.

Закон распределения дискретной случайной величины может быть задан с помощью таблицы, аналитически (с помощью формулы) и графически.

Простейшей формой задания дискретной случайной величины является таблица, в которой перечислены в порядке возрастания все возможные значения случайной величины и соответствующие им вероятности:

Х	x1	x2	…	xn-1	хn
P(X=xi)	p1	p2	…	pn-1	pn

здесь х_i – всевозможные значения случайной величины Х, р_i = P(X=x_i) – вероятность события, состоящего в том, что случайная величина Х примет значение x_i (1£i£n).

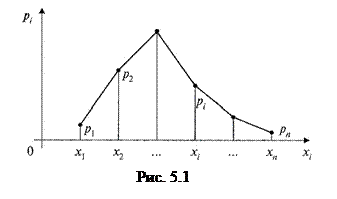Графически закон распределения может быть задан в виде ломаной, называемой многоугольником или полигоном распределения вероятностей (рис. 5.1)

Так как в результате испытания величина Х всегда примет одно из значений x₁, x₂,…, x_n, то

p₁+ p₂+…+ p_n=1.

Пример 5.2.1. В денежной лотерее разыгрывается 1 выигрыш в 100000р., 10 выигрышей по 10 000 р. и 100 выигрышей по 100 р. при общем числе билетов 10 000. Найти закон распределения случайного выигрыша Х для владельца одного лотерейного билета.

○ Здесь возможные значения для Х: х₁=0, х₂=100, х₃=10 000, х₄=100 000. Вероятности их будут: р₁=0,9889 (так как билетов без выигрыша 10000–(1+10+100)=9889), р₂=0,01, р₃=0,001, р₄=0,0001. Следовательно, закон распределения для выигрыша Х может быть задан таблицей:

Х			10 000	100 000
P(X=xi)	0,9889	0,01	0,001	0,0001

Проверим, действительно ли сумма полученных вероятностей равна 1.

Имеем: P(X=0)+P(X=100)+P(X=10000)+P(X=100000)=

=0,9889+0,01+0,001+0,0001=1. ●

5.2.2.2. Математическое ожидание дискретной случайной величины

Закон распределения полностью задает дискретную случайную величину. Однако часто встречаются случаи, когда закон распределения случайной величины неизвестен. В таких случаях случайную величину изучают по ее числовым характеристикам. Одной из таких характеристик является математическое ожидание.

Пусть некоторая случайная величина Х с конечным числом своих значений задана законом распределения:

Х	x1	x2	…	хn
P(X=xi)	p1	p2	…	pn

Определение 5.2.1.Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех возможных значений величины Х на соответствующие вероятности:

(5.2.1)

М(Х)= x₁p₁+ x₂p₂+…+ х_n p_n.

Пример 5.2.2.Найти математическое ожидание выигрыша Х из примера 5.2.1.

○Используя полученное в примере 5.2.1 распределение случайной величины Х, имеем:

М(Х)=0·0,9889+100·0,01+10 000·0,001+100 000·0,0001=1+10+20=21(р).

Очевидно, М(Х)=21 р. есть справедливая цена одного лотерейного билета.●

Теорема 5.2.1. Математическое ожидание дискретной случайной величины Х приближенно равно среднему арифметическому всех ее значений (при достаточно большом числе испытаний).

Примечание.Математическое ожидание случайной величины называют также ее средним значением или ожидаемым значением.

Свойства математического ожидания

Основные свойства

Некоторые законы распределения случайных величин

Дискретные и непрерывные случайные величины

Распределения случайных величин

Количественная характеристика опыта состоит в определении значений некоторых величин, полученных в результате опыта.

Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных (причем до опыта невозможно предвидеть – какое именно).

Случайные величины обозначают заглавными буквами Х, Y, Z, …, а их возможные значения – соответствующими строчными буквами x, y, z, ….

Если случайное событие полностью характеризуется вероятностью появления этого события, то описание вероятностных свойств случайных величин является более сложной задачей.

Вероятностные свойства случайных величин описываются законом распределения, т.е. соотношением, устанавливающим связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения полностью характеризует случайную величину.

Различают дискретные и непрерывные случайные величины.