Система уравнений Лоренца-Максвелла
Прежде всего, следует отметить, что уравнения электромагнитного поля или уравнения Лоренца-Максвелла являются выражением одного из фундаментальных законов природы и не могут быть выведены из других законов. Уравнения в частных производных, рассматривавшиеся в предыдущих главах были получены в результате формулирования (записи) известного закона физики для малого, но конечного объема (площади, отрезка) с последующим стягиванием этого малого объема в точку, что эквивалентно операции осреднения, что осуществимо только в условиях сплошной среды. В результате, входящие в полученные уравнения частные производные выражали некоторые средние, т.е. макроскопические, величины. Что касается уравнений Лоренца-Максвелла, то они изначально были сформулированы на микроскопическом уровне и характеризуют связь между входящими в них физическими величинами в каждой точке пространства.
Итак, система уравнений Лоренца-Максвелла имеют следующий вид
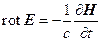 (1)
(1)
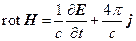 (2)
(2)
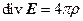 (3)
(3)
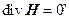 (4)
(4)
Эти уравнения связывают электрическое поле (напряженность) Е и магнитное поле (напряженность) Н между собой, а также с плотностью электрического заряда ρ и вектором плотности тока j. Величина с – электродинамическая постоянная, численно равная скорости света в вакууме.
Линии, в каждой точке которых, касательная совпадают с вектором электрического поля, называется линиями электрического поля. Аналогично определяется и линии магнитного поля. Те и другие называют силовыми линиями.
Продифференцировав по времени уравнение (3) и подставив туда после этого 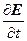 из (2), мы получим
из (2), мы получим
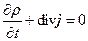 (5)
(5)
Это уравнение представляет собой закон сохранения электрического заряда. В этом можно убедиться, проинтегрировав уравнение (5) по некоторому произвольному объему V и применив ко второму слагаемому формулу Гаусса-Остроградского
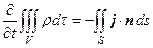 ,
,
т.е. приращение количества электричества в некотором объеме за единицу времени равно электрическому току, поступающему в этот объем (при условии, что n – внешняя нормаль).
Уравнение (3) констатирует, что источниками электрического поля являются электрические заряды, в то время как согласно уравнению (4) магнитное поле не имеет источников. В соответствии с этим число магнитных силовых линий, входящих в произвольный объем, всегда равен числу магнитных силовых линий, выходящих из него. Это, в свою очередь, означает, что магнитные силовые линии либо замкнуты, либо имеют бесконечную длину. Следует обратить внимание на уравнение (2). Оно обобщает известный закон Био-Савара за счет добавления члена 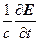 . Это добавления, произведенное в свое время Максвеллом, позволило замкнуть систему (1)–(4), которая в этом виде стала давать полное описание электромагнитного поля.
. Это добавления, произведенное в свое время Максвеллом, позволило замкнуть систему (1)–(4), которая в этом виде стала давать полное описание электромагнитного поля.
Важно также заметить, что, взяв дивергенцию от обеих частей уравнения (1), найдем, что
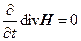 , (6)
, (6)
откуда следует, что
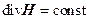
Сравнивая это выражение с уравнением (4) мы приходим к выводу, что оно лишь определяет константу интегрирования, которая равна нулю. Кроме того, это уравнение показывает, что, если 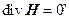 в некоторый начальный момент времени, то в соответствии с (6) это будет иметь место и во все последующие моменты времени.
в некоторый начальный момент времени, то в соответствии с (6) это будет иметь место и во все последующие моменты времени.
