Классификация квазилинейных уравнений второго порядка

Формулировка большинства традиционных задач физики приводит к линейным уравнениям в частных производных второго порядка с постоянными коэффициентами.

Так, при изучении различных видов волн, а также других колебательных явлений мы приходим к так называемому волновому уравнению

(3)

Процессы распространения тепла в однородном теле, так же как и явления диффузии описываются уравнением теплопроводности

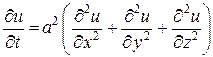(4)

При рассмотрении установившегося теплового состояния, электрического поля или поля тяготения мы приходим к уравнению Пуассона

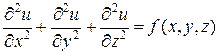(5)

При отсутствии источников тепла, электрических зарядов или масс уравнение (5) переходит к уравнению Лапласа

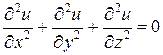(6)

Уравнения (3)–(6) являются линейными уравнениями второго порядка с постоянными коэффициентами. Их часто называют основными уравнениями математической физики.

Следует также привести уравнение, которым приходится пользоваться при описании некоторых волновых процессов и которое называется телеграфным уравнением

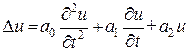, (7)

где 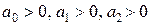. Это уравнение при 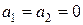переходит в волновое уравнение (3), при 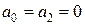в уравнение теплопроводности и диффузии (4), а при 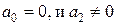в уравнение диффузии с химическими реакциями.

Каждое из уравнений (3) – (7) принадлежит к одному из трех типов. Тип уравнения определяется в некоторой фиксированной точке М₀ (x₀ , y₀ , z₀ , t₀). Определение типа уравнения удобнее всего сформулировать для квазилинейного уравнения второго порядка, записанного в следующем виде:

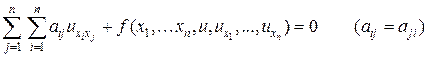(8)

где a_ij, и b_i – функции x₁,…x_n. При x=4 в качестве x₁,x₂,x₃ могут выступать пространственные координаты x,y,z, а в качестве x₄ – время t. Составив затем в фиксированной точке 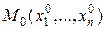квадратичную форму

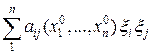(9)

Уравнение (7) в точке М₀ принадлежит к элептическому типу, если в этой точке квадратичная форма (8) является положительно или отрицательно определенной.

Уравнение (7) в точке М₀ принадлежит к гиперболическому типу, если в этой точке квадратичная форма (8) при приведении её к сумме квадратов имеет все коэффициенты, кроме одного, одного, определенного знака, а оставшийся один коэффициент противоположного знака.

Уравнение (7) в точке М₀ принадлежит к параболичекому типу, если в этой точке квадратичная форма (8) при приведении её к сумме квадратов имеет только один коэффициент, равный нулю, а все другие коэффициенты имеют одинаковые знаки.

Посколькукоэффициенты a_ij, и b_i являются функциями x₁,…x_n, то при переходе от одной точки к другой уравнение (7) может менять свою принадлежность к тому или иному типу. В связи с этим, уравнение принадлежит к тому или иному типу в некоторой области D, если оно принадлежит к этому типу в каждой точке этой области.

Для квазилинейного уравнения второго порядка с двумя независимыми переменными тип уравнения определяется более наглядно. Для этого его нужно записать в следующем виде:

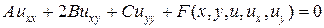(10)

где коэффициенты A,B и C есть функции x и y.

Уравнение (9) принадлежит

а) к гиперболическому типу, если ;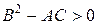

б) к параболическому типу, если ;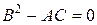

в) к эллиптическому типу, если .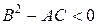

В записанных выше уравнениях (3) – (6) коэффициенты при производных являются постоянными, поэтому при переходе от одной точки к другой тип уравнения сохраняется. В связи с этим во всей области решения задачи уравнение (3) является уравнением гиперболического типа, уравнение (4) – уравнением параболического типа, а уравнения (5) и (6) уравнениями элептического типа.

Г л а в а I. Скалярные и векторные поля. Дифференциальные операторы

Скалярные поля

Цель этой короткой главы – лишь напомнить некоторые понятия, результаты, их математические формулировки и физический смысл, которые излагаются в курсе математического анализа, и которые потребуются нам в дальнейшем при изложении материала. Это касается понятий скалярного и векторного полей, а также дифференциальных операторов, применяемых к этим полям.

Наряду с понятием скалярной и векторной физической величины в математической физике часто пользуются понятиями скалярного поля и векторного поля.

Если в каждой точке М области D задано значение скалярной величины u, то эта величина является скалярной функцией точки, т.е. 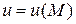. В этом случае говорят, что в области D задано скалярное поле.

Для скалярного поля вводится понятие поверхности уровня, которая определяется как геометрическое место точек, в которых функция u имеет постоянное значение. В трехмерном случае это можно записать как

.

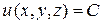Градиент скалярной величины

Наряду с понятием поверхности уровня вводится понятие градиента, т.е. векторной величины, направление которой совпадает с направлением нормали к поверхности уровня скалярного поля (Рис. 1). Проекциями этого вектора на координатные оси служат частные производные от функции 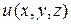, т. е. :

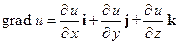. (1)

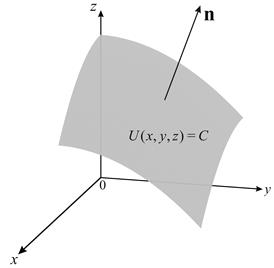
Рис. 1. К понятию градиента скалярной функции

Таким образом, градиент это вектор, который представляет собой результат применения некоего дифференциального оператора к скалярной функции.

Если векторное поле Ав каждой точке М может быть задано как градиент некоторой функции U, т. е. А=grad U, то такое поле называют потенциальным, а функцию U – потенциалом.

Физический смысл градиента заключается в том, что его направление совпадает с направлением наибольшего возрастания скалярной величины. Так градиент температуры направлен к источнику тепла, а градиент потенциала электростатического поля к одиночному заряду и т.д. Модуль градиента характеризует степень возрастания скалярной величины.

Векторные поля

Если в каждой точке М области D задан определенный вектор А(М), то говорят, что в области D задано векторное поле. Примерами векторных физических полей служат гравитационное поле, электромагнитное поле, поле скоростей текущей жидкости и т.д.

Для векторного поля вводят понятие векторной линии, т.е. линии, направление касательной к которой в каждой точке совпадает с направлением вектора А(М) (Рис. 2).

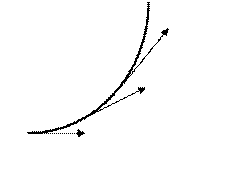Если векторное поле определяется функцией

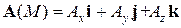, (2)

то векторная линия в пространстве задается следующей системой дифференциальных уравнений

Рис. 2. К понятию векторной линии

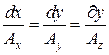. (3)

Поток вектора

Важным понятием для векторного поля является поток вектора. Если векторное поле задано выражением (2), то для всякой поверхности S с нормалью n можно записать интеграл по этой поверхности от проекции вектора A на нормаль n, а именно

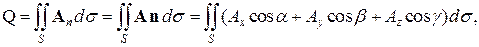(4)

где α, β, γ – направляющие косинусы нормали. Формула (4) и определяет поток вектора Aчерез поверхность S.

Физический смысл потока нагляднее всего иллюстрируется на примере потока жидкости, который есть не что иное, как объём жидкости, пересекающий единицу поверхности в единицу времени. Тогда поток жидкости через площадку dS будет равен объему параллелепипеда с ребром, равным скорости потока Vи высотой, равной V_n (см. Рис. 3), а поток жидкости через всю поверхность S будет соответственно равен

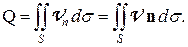(5)

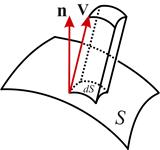
Рис. 3. К физическому смыслу потока вектора

Дивергенция вектора

Понятие потока вектора лежит в основе другого важного понятия – дивергенции вектора. Для его определения нужно рассмотреть некоторую точку векторного поля А(M) и окружить её замкнутой поверхностью S, целиком содержащейся в поле. В поле скоростей жидкости это будет соответствовать алгебраической сумме втекающей и вытекающей жидкости, которая будет равна нулю, если внутри объема отсутствуют источники и стоки жидкости.

Теперь возьмем отношение потока вектора Ак объему V внутри поверхности S

,

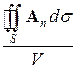и найдем предел этого отношения при V, стремящемся к нулю. Этот предел и называется дивергенцией или расходимостью вектораА в точке М, а именно

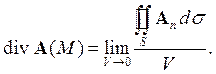(6)

Дифференциальная форма дивергенции векторного поля, заданного формулой (2), имеет вид:

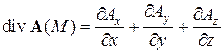. (7)

Таким образом, результат применения оператора дивергенции к вектору является величиной скалярной.

Пользуясь выражением для дивергенции (7), теорему Остроградского можно записать в векторном виде

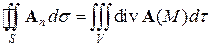(8)

Эта форма теоремы Остроградского для поля текущей жидкости выражает тот очевидный факт, что поток жидкости через поверхность равен суммарной мощности всех источников и стоков, т.е. количеству жидкости, возникающей в рассматриваемой области в единицу времени.