Тема: «Применение производных к исследованию функций».

Знания:

- определение возрастающей и убывающей функций;

- необходимый и достаточный признаки убывания и возрастания функции;

- определение точек максимума и минимума функций;

- понятие точек экстремума функции;

- необходимое и достаточное условия существования точек экстремума;

- понятие выпуклости и вогнутости функции, точек перегиба.

Умения:

- находить интервалы убывания и возрастания функции, точки экстремума;

- находить интервалы выпуклости и вогнутости функции, точки перегиба;

- исследовать функцию и строить ее график.

Задание 1.

Исследовать средствами дифференциального исчисления функции и построить их графики.

1.		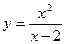	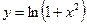11.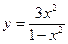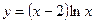
2.		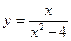	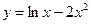12.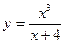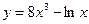
3.		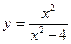	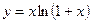13.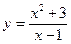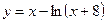
4.		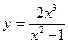	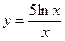14.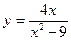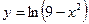
5.		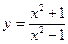	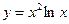15.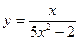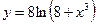
6.		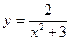	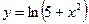16.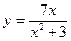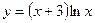
7.		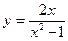	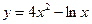17.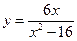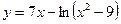
8.		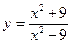	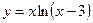18.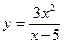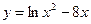
9.		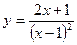	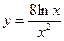19.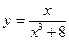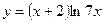
10.		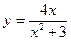	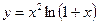20.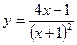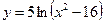

Лабораторная работа №4

Тема: «Неопределенный и определенный интегралы. Применение определенного интеграла к решению прикладных задач. Дифференциальные уравнения »

Знания:

- определение первообразной функции;

- определение неопределенного интеграла;

- свойства неопределенного интеграла;

- таблицу неопределенных интегралов;

- методы интегрирования;

- свойства определенного интеграла;

- формулу Ньютона-Лейбница для вычисления определенных интегралов;

- основные понятия теории дифференциальных уравнений.

Умения:

- находить неопределенный интеграл различными методами;

- применять формулу Ньютона-Лейбница для вычисления определенного интеграла;

- находить общее и частное решение дифференциальных уравнений.

Задание 1.

Вычислить следующие интегралы.

1.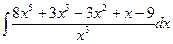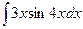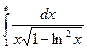
2.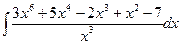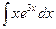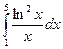
3.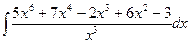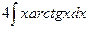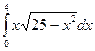
4.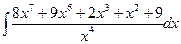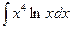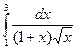
5.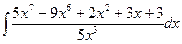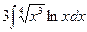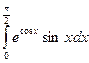
6.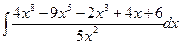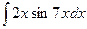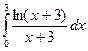
7.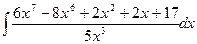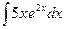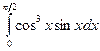
8.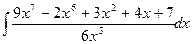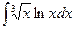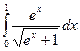
9.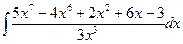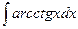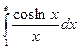
10.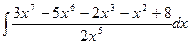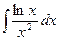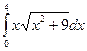
11.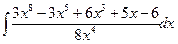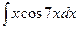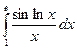
12.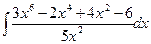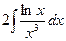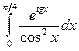
13.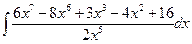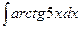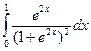
14.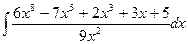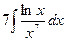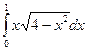
15.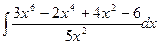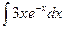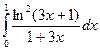
16.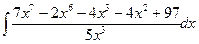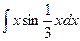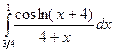
17.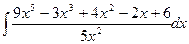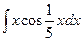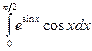
18.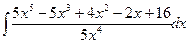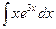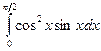
19.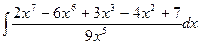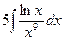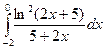
20.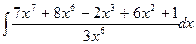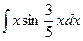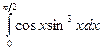

Задание 2.

1. Вычислить площадь фигуры, ограниченной линиями: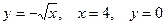

2. Вычислить работу переменной силы 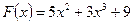при перемещении материальной точки вдоль оси абсцисс из положения с абсциссой 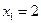в положение с абсциссой .

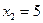3. Скорость прямолинейного движения тела выражается формулой 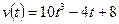(м/с). Найти путь, пройденный телом за 8 секунд от начала движения.

4. Вычислить площадь фигуры, ограниченной линиями: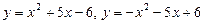

5. Вычислить работу переменной силы 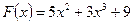при перемещении материальной точки вдоль оси абсцисс из положения с абсциссой 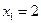в положение с абсциссой .

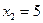6. Два тела начали двигаться одновременно из одной точки в одном направлении по прямой. Первое тело движется со скоростью 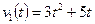м/с, второе – со скоростью 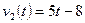м/с. На каком расстоянии друг от друга они окажутся через 15 с?

7. Вычислить площадь фигуры, ограниченной линиями: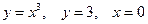

8. Вычислить объём тела, образованного вращением вокруг оси 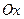фигуры, ограниченной линиями .

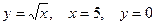9. Тело движется прямолинейно со скоростью 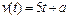(м/с). найти значение параметра 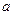, если известно, что за промежуток времени от 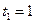до 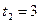(с) тело прошло путь длиной 50 м.

10. Вычислить площадь фигуры, ограниченной линиями: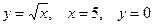

11. Вычислить работу переменной силы 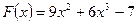при перемещении материальной точки вдоль оси абсцисс из положения с абсциссой 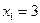в положение с абсциссой .

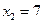12. Вычислить объём тела, образованного вращением вокруг оси 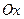фигуры, ограниченной линиями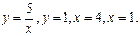

13. Вычислить площадь фигуры, ограниченной линиями: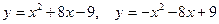

14. Вычислить работу переменной силы 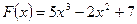при перемещении материальной точки вдоль оси абсцисс из положения с абсциссой 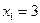в положение с абсциссой .

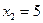15. Тело движется прямолинейно со скоростью 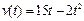(м/с). Найти длину пути, пройденного телом от начала пути, до его остановки. Указание: в моменты начала и остановки скорость тела равна нулю.

16.Вычислить площадь фигуры, ограниченной линиями: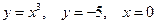

17. Вычислить работу переменной силы 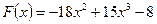при перемещении материальной точки вдоль оси абсцисс из положения с абсциссой 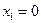в положение с абсциссой .

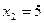18. Вычислить объём тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями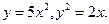

19. Вычислить площадь фигуры, ограниченной линиями: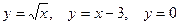

20. Вычислить объём тела, образованного вращением вокруг оси ох фигуры, ограниченной линиями: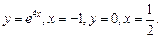

Задание 3.

Найти общее решение дифференциального уравнения первого порядка

1.		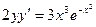	11.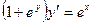
2.		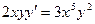	12.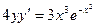
3.		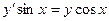	13.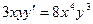
4.		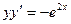	14.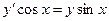
5.		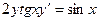	15.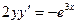
6.		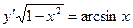	16.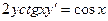
7.		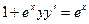	17.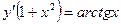
8.		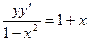	18.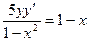
9.		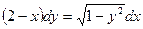	19.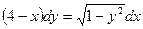
10.		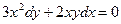	20.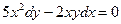

Задание 4.

Найти частное решение дифференциального уравнения первого порядка

1.	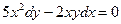,		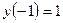11.	,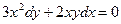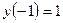
2.	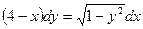,		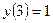12.	,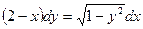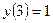
3.	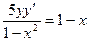,		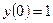13.	,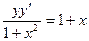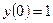
4.	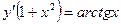,		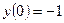14.	,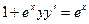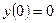
5.	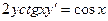,		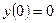15.	,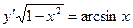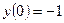
6.	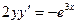,		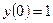16.	,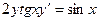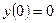
7.	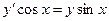,		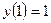17.	,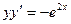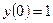
8.	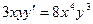,		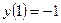18.	,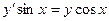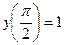
9.	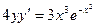,		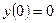19.	,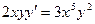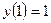
10.	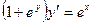,		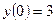20.	,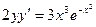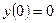

Лабораторная работа №5