Производная функции и её применение
Производная функции и её применение
Определение производной функции. Вычисление производных основных элементарных функций. Вычисление производных сложных функций
Пусть функция f(x) определена в некоторой окрестности точки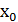 
.
Определение: Производной функции y=f(x) по аргументу x называется предел отношения ее приращения ∆f(x) к приращению ∆x аргумента x, когда приращение аргумента стремится к нулю:
.
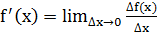Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этот предел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Алгоритм отыскания производной y = f(x):
1. Находим f(x).
2. Находим f(x+∆x).
3. Вычисляем ∆f = f(x+∆x) – f(x).
4. Составляем отношение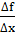 
при ∆x→0.
Пример 1. Найти производную функции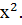 
Решение.
1) f(x) =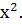 
2) f(x+∆x) =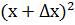 
.
3) ∆f = f(x+∆x) – f(x) =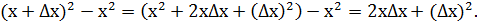 
4) 
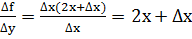
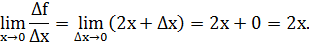
Итак,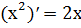 
.
Необходимое условие существования производной вытекает из следующей теоремы.
Теорема. Если функция f(x) дифференцируема в точке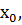 
то она непрерывна в этой точке.
Основные правила дифференцирования
Непосредственное вычисление производной функции с помощью предела в большинстве случаев представляет собой громоздкие вычисления. Значительно проще вычислять производные, применяя правила дифференцирования.
Обозначения: С−постоянная; х−аргумент; u, v, w−функции от х, имеющие производные.
Правило 1. Производная постоянной
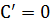
Правило 2. Производная произведения постоянной на функцию
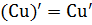
Правило 3. Производная алгебраической суммы
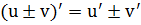
Правило 4. Производная произведения
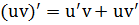
Правило 5. Производная частного (дроби)
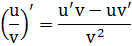
Частные случаи
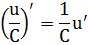
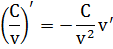
Таблица основных формул дифференцирования
1. 
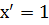
2. 
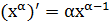
3. 
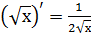
4. 
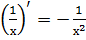
5. 
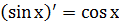
6. 
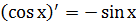
7. 
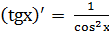
8. 
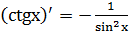
9. 
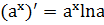
10. 
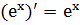
11. 
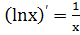
12. 
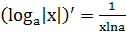
13. 
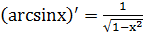
14. 
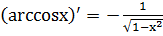
15. 
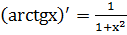
16. 
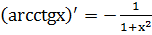
Пример 2. Найти производную функции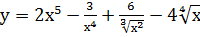 
.
Решение. Запишем формулу в виде
= 
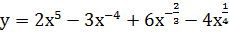
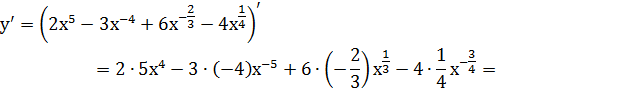
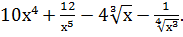
Пример 3. Найти производную функции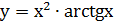 
.
Решение. Применяя правило производная произведения и формулы (2) и (15) получим
.
Пример 4. Найти производную функции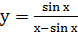 
.
Решение. Применяя правило производная частного и формулы (1) и (5) получим
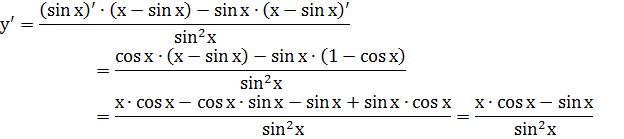
Производная сложной функции
Если переменная y зависит от переменной u, а переменная u в свою очередь от переменной x, т.е. y=f(u(x)), то y называют сложной функцией от x. Например, y=sin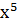 
– сложная функция от x, т.к. синус зависит от промежуточного аргумента х5.
Производная сложной функции определяется по формуле
,
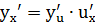т.е. производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную этого аргумента по независимой переменной. Аналогично формула верна и для сложных функций, которые задаются с помощью цепочки, содержащей три звена и более.
Пример 5. Найти производную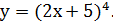 
Решение.
y’=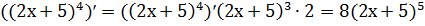 
.
Пример 6. Найти производную функции y=sin(3x-5).
Решение.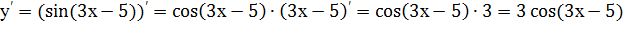 
.
Пример 7. Найти производную функции у=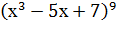 
.
Решение.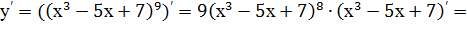 
.
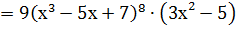Пример 8. Найти производную функции у=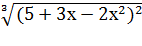 
.
Решение. Эта функция также является сложной степенной функцией, а именно у=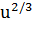 
, где u= 
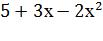. Поэтому
.
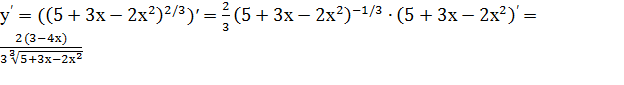Пример 9. Найти производную функции у=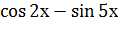 
.
Решение.
= 
.
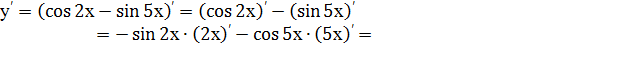
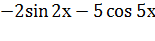Пример 10. Дана функция f(x)=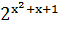 
. Найти 
.
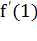Решение.
.
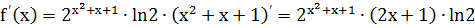Вычислим значение производной при х=1
,
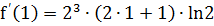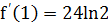. [1]
Упражнения для закрепления
1. 
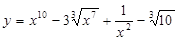
2. 
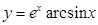
3. 
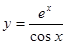
4. 
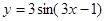
5. 
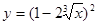
6. 
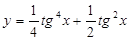
7. 
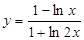
8. 
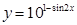
9. 
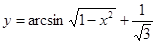
10. 
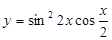
11. 
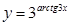
12. 
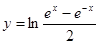
Контрольные вопросы
1. Дать определение производной функции.
2. Что называется приращением аргумента, приращением функции?
3. Как найти производную суммы или разности?
4. Как найти производную произведения?
5. Как найти производную частного двух функций?
6. Дать определение дифференциала функции.
Упражнения для закрепления
1. Составить уравнения касательной и нормали к линии у= 
в точке с абсциссой х=2.
2. Составить уравнения касательной и нормали к линии у=4х− 
в точке с абсциссой х=1.
3. Составить уравнения касательной и нормали к линии у= 
в точке с абсциссой х=−1.
4. Составить уравнения касательной и нормали к кривой у= 
в точке
(0; −2).
5. Найдите угол наклона касательной к графику функции f(x)= 
в точках х=0,5; х=1; х=1,5.
6. На графике функции f(x)= 
найдите точку, в которой касательная к нему образует с осью Ох угол π/4.
7. К графику функции f(x)= 
проведена касательная, параллельная оси абсцисс. Найдите координаты точки касания.
8. Найдите скорость и ускорение в указанные моменты времени для точки, движущейся прямолинейно, если движение точки задано уравнением s= 
, t=2.
9. Пуля вылетает из автомата вверх со скоростью 500м/с. Найдите скорость пути через 12с и определите, сколько времени поднимается вверх (сопротивление воздуха не учитывать).
10. Скорость прямолинейного движения тела выражается законом v=t2−4t+5 (v− в м/с, t− в секундах). В какой момент времени ускорение будет равно нулю?
11. Тело масса которого m=3кг, движется прямолинейно по закону s=t2+t+1 (s− в метрах, t−в секундах). Найдите кинетическую энергию тела (mv2/2) через 5с после начала движения.
12. Количество электричества, протекающее через проводник начиная с t=0, определяется по формуле Q=0,5t3+0,2t2+t+1 (Q− в кулонах, t− в секундах). Найдите силу тока при t=10с.
Контрольные вопросы
1. Какой механический смысл имеет производная?
2. Сформулировать геометрический смысл производной.
X x
Определение:Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции 
, характеризуется знаком ее второй производной: если в некотором промежутке 
, то кривая выпукла вниз на этом промежутке; если же 
, то кривая выпукла вверх на этом промежутке.
Определение. Точка графика функции , разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции , в которых вторая производная 
обращается в нуль или терпит разрыв.
Правило нахождения точек перегиба графика функции 
1. Найти вторую производную .
2. Найти критические точки II рода функции , т.е. точки, в которой обращается в нуль или терпит разрыв.
3. Исследовать знак второй производной в промежутка, на которые найденные критические точки делят область определения функции 
. Если при этом критическая точка 
разделяет промежутки выпуклости противоположных направлений, то является абсциссой точки перегиба графика функции.
4. Вычислить значения функции в точках перегиба.
Пример 3. Найти промежутки выпуклости и точки перегиба следующей кривой: 
.
Решение: Находим 
, 
.
Найдем критические точки по второй производной, решив уравнение 
, 
.
 |  |  | |
 | + | - | |
 | ↑ | точка перегиба | ↑ |
Ответ: Функция выпукла вверх при 
; функция выпукла вниз при 
; точка перегиба 
.
Упражнения для закрепления
1. Найти промежутки монотонности и экстремумы функции:
а) 
б) 
в) 
г) 
д) 
2. Найти промежутки выпуклости и точки перегиба следующей кривой:
а) 
б) 
в) 
г) 
д) 
3. Найти наибольшее и наименьшее значения функции:
а) 
на [0;1]
б) 
на [-2;3]
в) на [-1;1]
4. Исследовать функцию и построить ее график:
а)
б)
в) 
Контрольные вопросы
1. Что такое критические точки функции?
2. Сформулировать достаточные условия возрастания и убывания функции.
3. Какими точками отделяются промежутки возрастания от промежутков убывания функции?
4. Сформулируйте правила нахождения точек экстремума функции.
5. Сформулировать достаточное условие выпуклости функции. Приведите алгоритм нахождения промежутков выпуклости и точек перегиба.
Производная функции и её применение