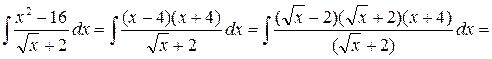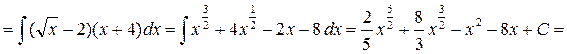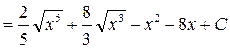Лекция 4. ОСНОВЫ ИНТЕГРИРОВАНИЯ
Вопросы:
1. Первообразная функции.
2. Свойства неопределенного интеграла.
3. Интегралы основных элементарных функций.
4. Непосредственное интегрирование.
5. Метод замены переменной (метод подстановки).
6. Интегрирование по частям
Первообразная функции
Основной задачей дифференциального исчисления является нахождение производной или дифференциала данной функции.
Интегральное счисление решает обратную задачу – нахождение самой функции по ее производной или дифференциалу.
Опр.: Функция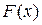 
называется первообразной функцией для функции 
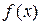на промежутке Х, если в каждой точке х этого промежутка
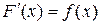
Например:
1) 
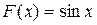является первообразной для функции 
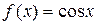, т.к.
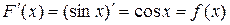
2. 
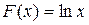на промежутке 
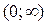для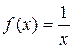 
, т.е.
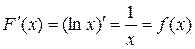
Исходя из геометрического смысла производной: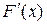 
– угловой коэффициент касательной к кривой 
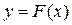в точке х
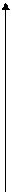Значит, найти первообразную для 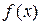– найти такую кривую 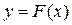, что угловой коэффициент касательной к ней в произвольной точке х равен значению 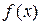заданной функции в этой точке
 |
Следует заметить, что для заданной функции 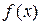ее первообразная определена неоднозначно.
Например:
Функции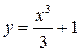 
, 
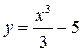и вообще функции 
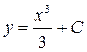, где С – некоторое действительное число, являются первообразными для функции
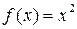
В общем случае, если 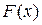– некоторая первообразная для 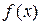, то поскольку
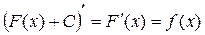
функции вида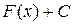 
, где С – произвольное число так же являются первообразными для .
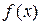Геометрически это означает, что если найдена одна кривая 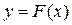, удовлетворяющая условию 
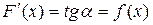, то сдвигая ее вдоль оси Оу, мы вновь получаем кривые, удовлетворяющие указанному условию (поскольку такой сдвиг не меняет углового коэффициента касательной).
Опр.: Совокупность всех первообразных для функции 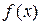на промежутке Х называется неопределенным интегралом от функции .
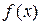Обозначение: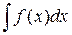 
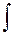– знак интеграла
х – переменная интегрирования
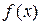– подинтегральная функция
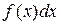– подинтегральное выражение
Пример:
1) 
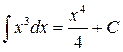
2) 
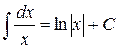
Операция нахождения неопределенного интеграла от некоторой функции называется интегрирование функции (обратная к операции дифференцирования).
Свойства неопределенного интеграла
1. Производная от неопределенного интеграла равна подинтегральной функции
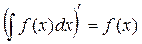
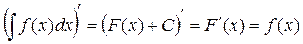
2. Дифференциал неопределенного интеграла равен подинтегральному выражению
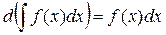
По определению дифференциала и свойству 1:
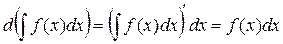
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.
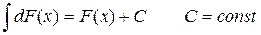
Доказательство:
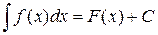
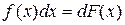
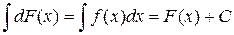
4. Постоянный множитель можно выносить за знак интеграла, т.е.
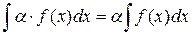
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.
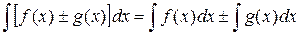
Таблица интегралов основных элементарных функций
1. 
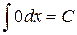
2. 
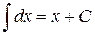
3. 
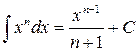
4. 
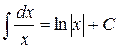
5. 
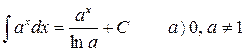
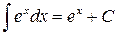
6. 
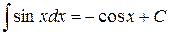
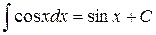
7. 
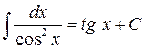
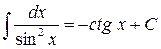
8. 
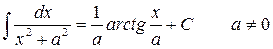
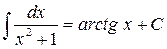
9. 
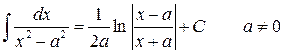
10. 
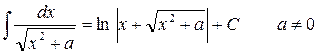
11. 
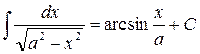
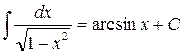
Справедливость приведенных формул проверяется дифференцированием:
Пример:
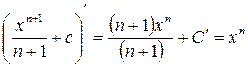
Примеры:
1. 
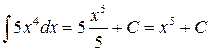
2. 
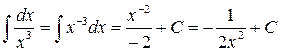
3. 
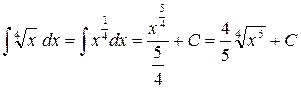
4. 
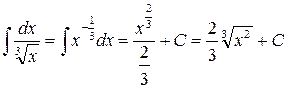
5. 
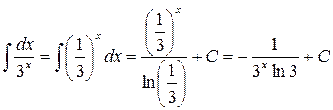
6. 
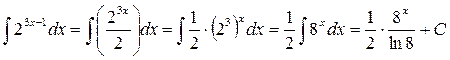
7. 
