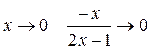Предел числовой последовательности
Опр.: Если по некоторому закону каждому натуральному числу n поставлено в соответствие число an, то говорят, что задана числовая последовательность 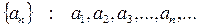
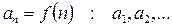 – элементы числовой последовательности.
– элементы числовой последовательности.
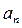 – общий член или n-ый член.
– общий член или n-ый член.
Рассмотрим 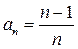
Опр.: Число А называется пределом числовой последовательности 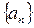 , если
, если 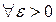 найдется такой номер N (зависящий от
найдется такой номер N (зависящий от 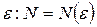 , что для всех элементов последовательности с номерами n > N верно неравенство:
, что для всех элементов последовательности с номерами n > N верно неравенство: 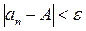
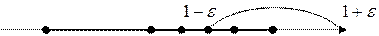 | |||
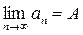 | |||
0 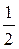
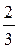
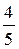
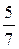 1
1
Геометрический смысл: Число A – есть 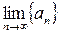 , если
, если 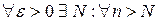 все члены
все члены 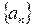 будут заключены в ε-окрестность точки А, какой бы узкой она не была. Вне этой окрестности – только конечное число членов
будут заключены в ε-окрестность точки А, какой бы узкой она не была. Вне этой окрестности – только конечное число членов 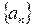 .
.
Опр.: Последовательность называется сходящейся если существует конечный предел этой последовательности, в противном случае последовательность называется расходящейся.
Предел функции в бесконечности и в точке
 Опр.: Число А называется пределом функции
Опр.: Число А называется пределом функции 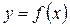 при х сходящемся к а, если
при х сходящемся к а, если 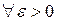 найдется такое
найдется такое 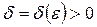 , что при
, что при 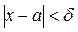 выполняется
выполняется 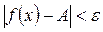 .
.
Обозначение: 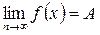
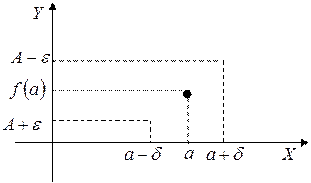 |
В определении не требуется, чтобы функция была определена и в предельной точке, но она должна быть определена в какой-либо окрестности предельной точки (за вычетом самой предельной точки).
Опр.: Если 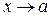 и
и 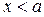 , то пишут
, то пишут 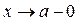 ; если
; если 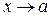 и
и 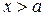 , то пишут
, то пишут 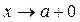 . Соответствующие пределы:
. Соответствующие пределы:
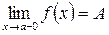 и
и 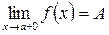
называются левосторонними и правосторонними пределами функции в точке а.
Для существования двухстороннего предела функции 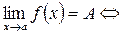 что существовали
что существовали 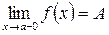 и
и 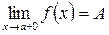 и они совпадали.
и они совпадали.
Если функция является элементарной и ее предельные значения аргумента (а) принадлежит ее области определения, то вычисление предела функции сводится к подстановке предельного значения аргумента, т.е.
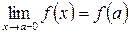 если
если 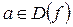
Опр.: Число В называется пределом функции в ∞, если 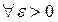 найдется такое число S, что
найдется такое число S, что 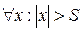 выполняется неравенство
выполняется неравенство 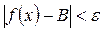 .
.

Основные теоремы о пределах
Бесконечно большая величина – переменная, предел которой равен + ∞ или
– ∞.
Бесконечно малая величина – переменная, предел которой равен 0.
Свойства:
1. 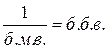 и
и 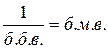
2. Если а и b – б.м.в., то
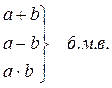
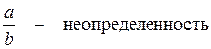
3. Если а и b – б.б.в., то
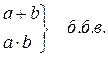
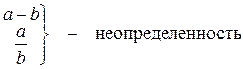
Теорема 1: Предел постоянной равен самой этой постоянной, т.к. если
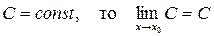
Теорема 2: Пусть существует 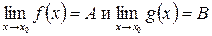 , тогда
, тогда
1) 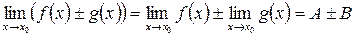
2) 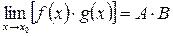
3) Если В ≠ 0, то 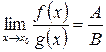
Лемма («о двух милиционерах»)
Если функции 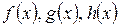 удовлетворяют условию
удовлетворяют условию 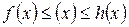 и если
и если 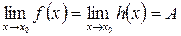 , то
, то 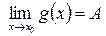 .
.
Примеры: вычисления пределов и раскрытие неопределенностей
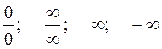
1. 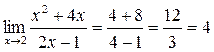
2. 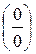
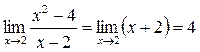
3. 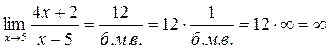
4. 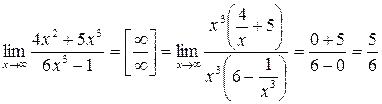
5. 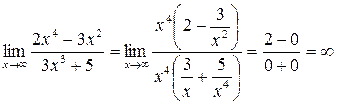
6. 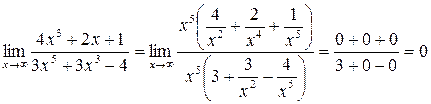
7. 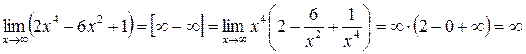
Замечательные пределы
Первый замечательный предел 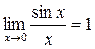
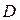
 Доказательство:
Доказательство:
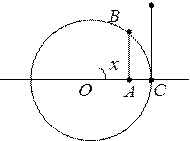 | ||||
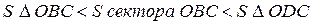 | ||||
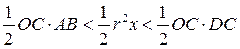 | ||||
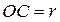
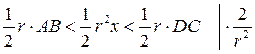
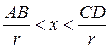
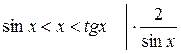
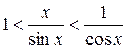
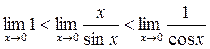
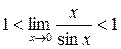
по лемме о двух милиционерах:
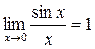
Второй замечательный предел 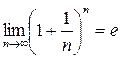
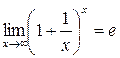
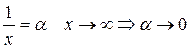
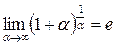
Функция 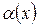 называется бесконечно малой функцией при
называется бесконечно малой функцией при 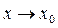 , если
, если
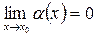
Если 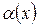 и
и 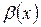 – б.м.ф., то
– б.м.ф., то
1) 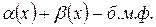
2) 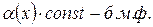
3) произведение б.м.ф. на ограниченную функцию есть б.м.ф.
Бесконечно большая функция 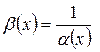
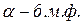
Опр.: Две функции 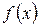 и
и 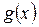 называются эквивалентными при
называются эквивалентными при 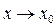 , если
, если 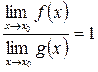 обозначается
обозначается 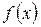 ∼
∼ 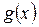
Пример:
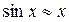
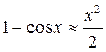
при 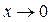
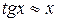
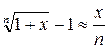
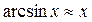
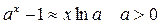
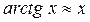
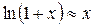
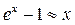
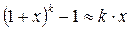
Непрерывность функции
Опр.: Функция 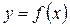 называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки и
называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки и 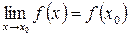
 |
Функция называется непрерывной слева (справа) в точке 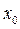 , если она определена в некоторой окрестности слева (справа) от точки
, если она определена в некоторой окрестности слева (справа) от точки 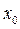 и
и
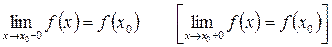
Опр.: Функция называется непрерывной в интервале, если она непрерывна в каждой точке этого интервала.
Опр.: Точки, в которых, функция не является непрерывной называются точками разрыва.
 Классификация точек разрыва
Классификация точек разрыва
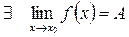


 1.
1.
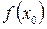

 Если
Если
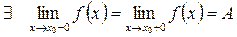 |
т.е.
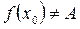 |
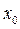
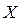
 но
но
(если в точке 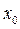 функция не определена)
функция не определена)
то 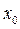 – точка устранимого разрыва I-го разряда.
– точка устранимого разрыва I-го разряда.
Пример:
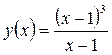 при
при 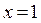 функция неопределенна.
функция неопределенна.
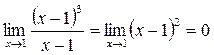
т.о. 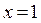 – точка устраняемого разрыва 1-го рода.
– точка устраняемого разрыва 1-го рода.
Доопределив функцию в токе 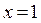 , получим:
, получим:
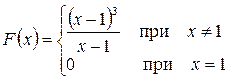
Новая функция будет уже непрерывна в точке 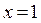 .
.
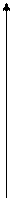 2.
2.
 | ||||||||
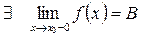 | ||||||||
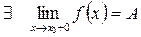 | ||||||||
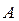 | ||||||||
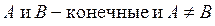 | 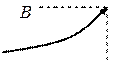 | |||||||
то 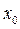 – точка конечного разрыва I-го рода.
– точка конечного разрыва I-го рода. 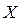
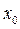
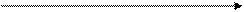
Опр.: Скачком функции в точке разрыва I-го рода называется величина:
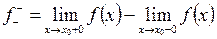
Пример:
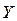

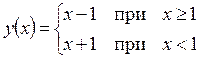
 при
при 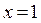
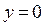
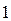


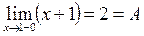
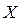
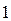

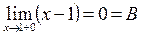
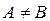 в точке
в точке 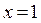 разрыв I рода.
разрыв I рода.
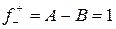
3.Все остальные – точки разрыва II рода.
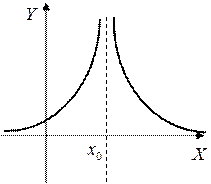 | 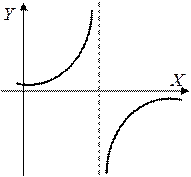 | 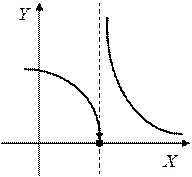 | |||
Пример:
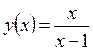 при
при 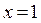 функция неопределенна
функция неопределенна
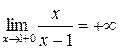
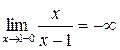
Т.к. односторонние пределы (достаточно было бы одного) бесконечны, то 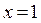 – точка разрыва II-го рода.
– точка разрыва II-го рода.
Примеры вычисления замечательных приделов:
1. 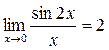 т.к.
т.к. 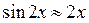
2. 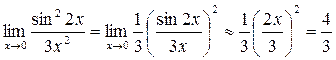
3. 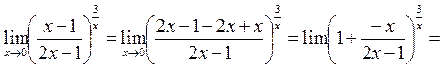
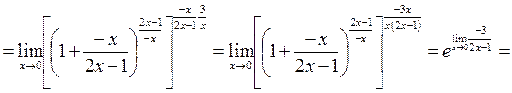
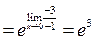
т.к. 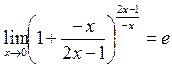 при
при