Алгоритм симплекс-метода для задачи на минимум

Шаг 0. Подготовительный этап.

Приводим задачу ЛП к специальной форме (15).

Шаг 1. Составляем симплекс-таблицу, соответствующую специальной форме:

	B		…		…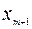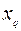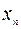
L			…		…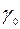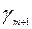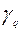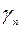
			…		…
..	..	…………
			…		…
..	..	…………
			…		…

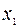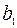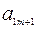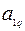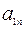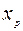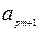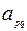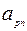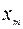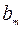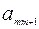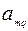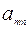Заметим, что этой таблице соответствует допустимое базисное решение 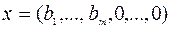задачи (15). Значение целевой функции на этом решении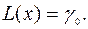

Шаг 2. Проверка на оптимальность

Если среди элементов индексной строки симплекс – таблицы 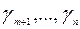нет ни одного положительного элемента то 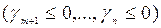, оптимальное решение задачи ЛП найдено: 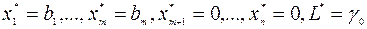. Алгоритм завершает работу.

Шаг 3. Проверка на неразрешимость

Если среди 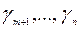есть положительный элемент 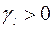, а в соответствующем столбце 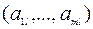нет ни одного положительного элемента 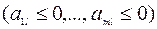, то целевая функция L является неограниченной снизу на допустимом множестве. В этом случае оптимального решения не существует. Алгоритм завершает работу.

Шаг 4. Выбор ведущего столбца q

Среди элементов 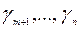выбираем максимальный положительный элемент 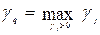.Этот столбец объявляем ведущим (разрешающим).

Шаг 5. Выбор ведущей строки p

Среди положительных элементов столбца 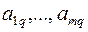находим элемент 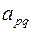, для которого выполняется равенство

.

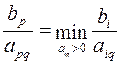Строку p объявляем ведущей (разрешающей). Элемент 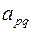объявляем ведущим (разрешающим).

Шаг 6. Преобразование симплексной таблицы

Составляем новую симплекс-таблицу, в которой:

а) вместо базисной переменной 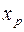записываем 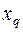, вместо небазисной пере менной 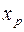записываем ;

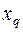б) ведущий элемент заменяем обратной величиной ;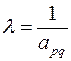

в) все элементы ведущего столбца (кроме 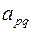) умножаем на ;

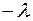г) все элементы ведущей строки (кроме 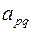) умножаем на ;

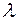д) оставшиеся элементы симплексной таблицы преобразуются по следующей схеме «прямоугольника».

Из элемента вычитается произведение трех сомножителей:

первый – соответствующий элемент ведущего столбца;

второй – соответствующий элемент ведущей строки;

третий – обратная величина ведущего элемента .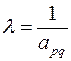

Преобразуемый элемент и соответствующие ему три сомножителя как раз и являются вершинами «прямоугольника».

Шаг 7. Переход к следующей итерации осуществляется возвратом к шагу 2.

Алгоритм симплекс-метода для задачи на максимум

Алгоритм симплекс-метода для задачи на максимум отличается от алгоритма для задачи на минимум только знаками индексной строки коэффициентов в целевой функции 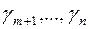, а именно:

На шаге 2: :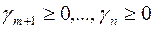

На шаге 3 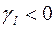. Целевая функция является неограниченной сверху на допустимом множестве.

На шаге 4: .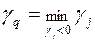

Пример решения задачи симплекс-методом

Решить задачу, записанную в виде (15).

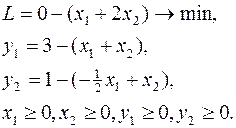
Составим симплексную таблицу:

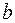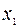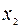L

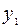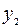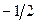Так как коэффициенты строки целевой функции неотрицательны, то начальное базисное решение 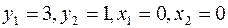не является оптимальным. Значение целевой функции для этого базиса L=0.

Выбираем ведущий столбец – это столбец, соответствующий переменной .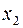

Выбираем ведущую строку. Для этого находим 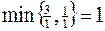. Следовательно, ведущая строка соответствует переменной .

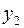Проводим преобразование симплексной таблицы, вводя переменную 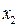в базис и выводя переменную 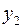из базиса. Получим таблицу:

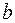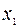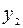L	-2		-2
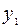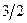			-1

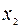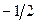Одна итерация метода завершена. Переходим к новой итерации. Полученная таблица неоптимальная. Базисное решение, соответствующее таблице, имеет вид 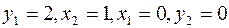. Значение целевой функции на этом базисе L= -2.

Ведущий столбец здесь – столбец, соответствующий переменной 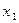. Ведущая строка – строка, соответствующая переменной 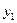. После проведения преобразований получим симплексную таблицу:

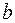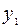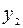L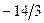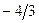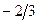

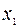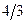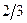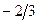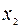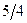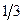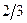Еще одна итерация завершена. Переходим к новой итерации.

Строка целевой функции не содержит положительных значений, значит, соответствующее базисное решение 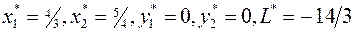является оптимальным, и алгоритм завершает работу.

Метод искусственного базиса

Симплекс-метод применяется для решения задач ЛП, представленных в специальной форме:

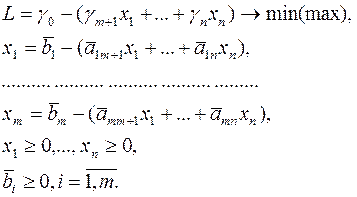(16)

Характерная особенность задачи (16) – известное базисное допустимое решение

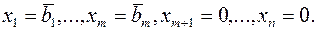
Чтобы применить симплекс-метод для решения задачи ЛП в произвольной форме, необходимо привести эту задачу к виду (16), т. е. выделить начальное допустимое базисное решение. Для этого в симплекс-метод вводят подготовительный этап. Один из методов для реализации подготовительного этапа называется методом искусственного базиса и состоит в следующем [1,2,3].

Вычислительная схема метода искусственного базиса

Шаг 1. Приводим задачу ЛП к канонической форме с неотрицательными правыми частями :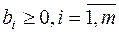

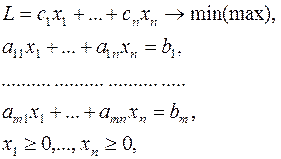(17)

Шаг 2. В каждую i-ю строку ограничений (17) вводим искусственную неотрицательную переменную 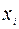и строим вспомогательную задачу ЛП вида:

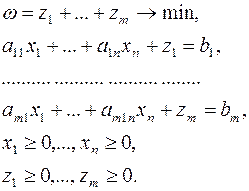(18)

В задаче (18) 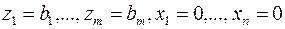– допустимое базисное решение, и задача (18) легко может быть сведена к виду (16). Для этого целевую функцию необходимо выразить через свободные переменные :

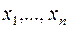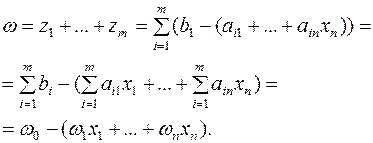
Шаг 3. Для вспомогательной задачи (18) строим симплексную таблицу

	b		…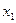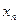
			…
			…
…	…	………………….
			…

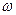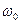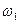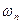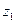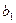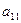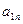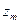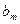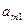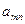и находим оптимальное решение вспомогательной задачи с помощью симплекс-метода.

Шаг 4. Если 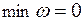и все переменные 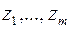являются небазисными, то m переменных из 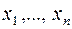войдут в базис и система ограничений, соответствующих симплексной таблице, будет иметь вид

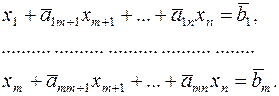(19)

Так как переменные 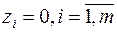, то их исключили из системы (19), не нарушив при этом равенств. Выражая целевую функцию основной задачи 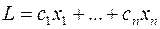через небазисные переменные 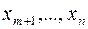системы (19), получим исходную задачу (17) в виде (16).

Шаг 5. Если 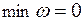, но в базисе остались искусственные переменные 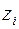, для которых 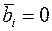(вырожденный случай), то проводим для каждой искусственной переменной 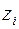из базиса следующее преобразование симплексной таблицы.

Выбираем ведущим столбцом столбец такой переменной 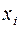, для которой элемент индексной строки 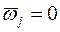, а элемент столбца 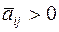. В этом случае строка искусственной переменной 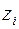будет ведущей и после стандартного преобразования симплексной таблицы (шаг 6 из прямого симплекс-метода) искусственная переменная 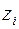выведется из базиса. В результате получим симплексную таблицу, соответствующую шагу 4.

Шаг 6. Если 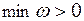, то допустимого решения в исходной задаче (17) не существует (не могут все искусственные переменные 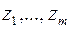быть равными нулю в задаче (18), а значит система ограничений задачи (17) несовместна) – процесс решения исходной задачи (17) завершается.

Пример решения задачи методом искусственного базиса

Выделить допустимое базисное решение для задачи ЛП:

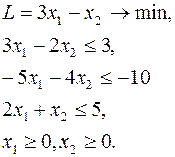
Приведем задачу к канонической форме на минимум с неотрицательными правыми частями:

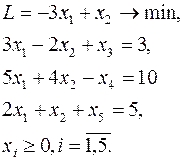
Заметим, что переменные 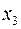и 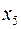можно использовать для введения в исходный базис, поэтому в первую и третью строку ограничений можно не вводить искусственные переменные.

Во вторую строку ограничений вводим искусственную переменную z, потому что в этой строке нет переменной, которую можно взять базисной, не проводя при этом дополнительных преобразований всей системы ограничений.

Полученная вспомогательная задача имеет вид

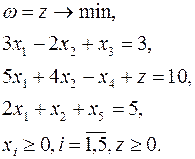
Приведем задачу к виду (16):

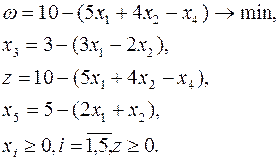
Выпишем соответствующую симплексную таблицу:

	B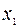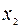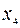
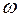				-1
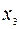			-2
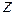				-1

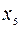Ведущий столбец рекомендуется выбирать не по максимальному положительному элементу строки целевой функции, а так, чтобы из базиса выводилась искусственная базисная переменная (соответствующая ведущая строка должна быть строкой искусственной переменной). Так, выбрав ведущим столбцом столбец переменной 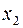, получим ведущую строку – строку с переменной z (выбирая ведущим столбцом 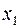, получили бы ведущую строку 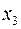, и из базиса выводилась бы переменная ).

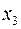Итак, искусственная переменная z выйдет из базиса, а переменная 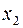введется в базис.

Симплексная таблица преобразуется к виду:

	B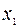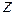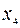
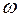			-1
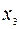		11/2	1/2	-1/2
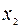	5/2	5/4	1/4	-1/4
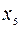	5/2	3/4	-1/4	1/4

Так как значение 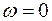, то полученный базис 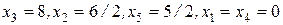является начальным допустимым базисом для исходной задачи ЛП. Чтобы выразить целевую функцию 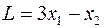через небазисные переменные 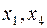, подставим значение базисной переменной 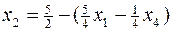в целевую функцию. В результате получим:

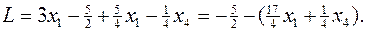
Тогда исходная задача будет иметь вид специальной формы задачи ЛП:

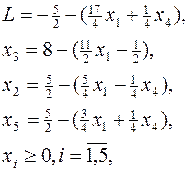
что и требовалось получить в результате решения вспомогательной задачи.

Двойственный симплекс-метод

Метод работает с теми же симплексными таблицами, что и прямой симплекс-метод для задачи на минимум. Сначала определяется переменная, подлежащая выводу из базиса, а затем переменная, вводимая в базис [1,3].

Вычислительная схема двойственного симплекс-метода

Шаг 0. Начинаем с симплексной таблицы, где .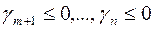

	B		…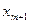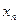
L			…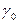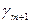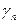
			…
…	…	…………..
			…

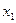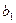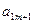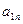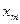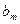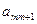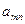Шаг 1. Проверка на оптимальность. Если 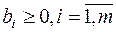, то решение 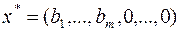– оптимальное.

Шаг 2. Выбор ведущей строки. Выбираем среди номеров i, для которых 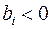, номер k с максимальным по модулю значением

.

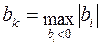Строка k объявляется ведущей.

Шаг 3. Проверка на неразрешимость. Если в строке 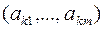нет отрицательных элементов, то двойственная целевая функция неограниченная и, следовательно, прямая задача не имеет допустимых решений. Процесс решения завершается.

Шаг 4. Выбор ведущего столбца s. Выбираем среди отрицательных элементов строки 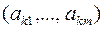элемент с номером s, для которого выполняется равенство

.

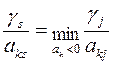Столбец s объявляется ведущим, а элемент 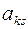– ведущим элементом.

Шаг 5. Проводим стандартное преобразование симплексной таблицы (Шаг 6 из прямого симплекс-метода).

Пример решения задачи двойственным симплекс-методом

Решить задачу ЛП двойственным симплекс-методом:

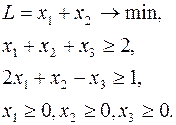
Приводим задачу к каноническому виду:

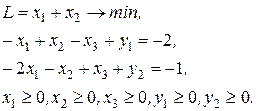
Знаки в ограничениях заменили противоположными для того, чтобы переменные 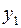и 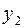можно было взять в качестве базисных. Симплексная таблица имеет вид

	b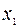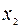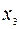
L		-1	-1
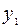	-2	-1		-1
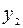	-1	-2	-1

Таблица двойственно-допустимая, но не оптимальная. Выбираем ведущую строку – это строка переменной 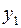, ведущий столбец – это столбец переменной 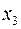. После преобразования таблица принимает вид

	b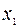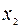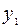
L		-1	-1
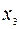			-1	-1
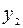	-3	-3

Так как в столбце b есть отрицательная переменная 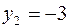, то эту строку выбираем ведущей, а столбец переменной 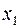будет ведущим столбцом. После преобразования получаем таблицу:

	b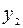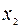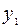
L		-1/3	-1	-1/3
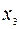		1/3	-1	-2/3
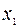		-1/3		-1/3

которая является оптимальной. Соответствующее оптимальное решение имеет вид .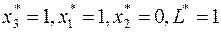

Двойственность в ЛП

Постановка задачи

Рассмотрим пару задач ЛП вида:

(I) (II)

… …

… …

… …

… …

.

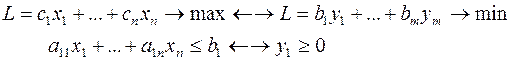
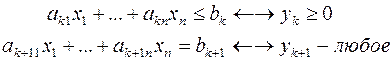
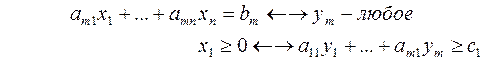
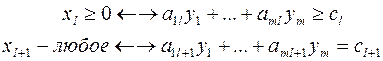
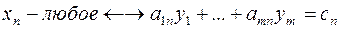Задачу (I) называют прямой задачей ЛП, а (II) – двойственной. Неравенства задач (I) и (II), соответствующие друг другу (по стрелке), называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т. е. соотношение двойственности взаимное. Поэтому можно из такой пары задач любую считать прямой, а другую – двойственной.

Пример построения двойственной задачи

Построить двойственную задачу к следующей задаче ЛП:

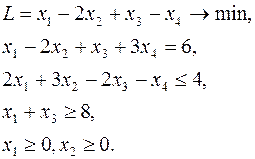
Прежде чем приступать к построению двойственной задачи, необходимо упорядочить запись исходной: согласовать знаки неравенств в ограничениях задачи с целевой функцией. Так как ЦФ минимизируется, то неравенства должны быть записаны с помощью знака « 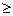». Для этого второе неравенство умножим на -1:

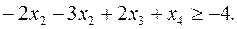
Теперь, вводя двойственные переменные 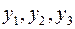, запишем в соответствии с указанным правилом пару двойственных задач:

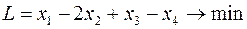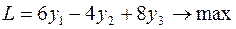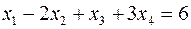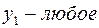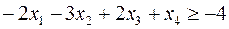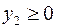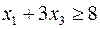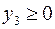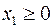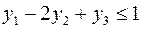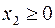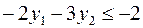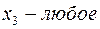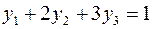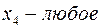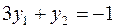Задача слева – исходная прямая задача, задача справа – двойственная к исходной задаче.

Теоремы двойственности

Двойственность является одним из фундаментальных понятий в теории ЛП. Исключительно важную роль играют следующие утверждения, получившие названия теорем двойственности [1,3].

Первая теорема двойственности. Если одна из пары двойственных задач (I) и (II) разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают:

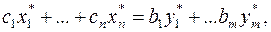
где 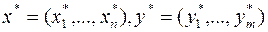– оптимальные планы задач (I) и (II) соответственно.

Говорят, что допустимые решения x, y удовлетворяют условиям дополняющей нежесткости (УДН), если при подстановке этих векторов в ограничения задач (I) и (II) хотя бы одно из любой пары сопряженных неравенств обращается в равенство.

Вторая теорема двойственности. 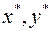оптимальны в задачах (I) и (II) тогда и только тогда, когда они удовлетворяют УДН.

Пример решения пары двойственных задач

Используя теоремы двойственности, решить двойственную задачу, если известно решение прямой задачи:

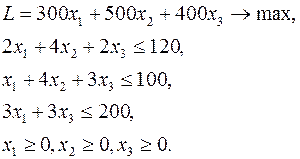(20)

Пусть решение задачи найдено одним из стандартных методов: 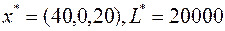. Построим двойственную задачу:

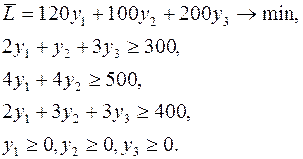(21)

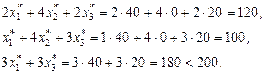По первой теореме двойственности задача разрешима, причем 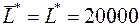. Найдем оптимальный план 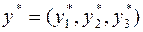задачи (21), используя вторую теорему двойственности. Подставим координаты вектора 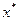в ограничения задачи (20). Получим

Следовательно, в силу УДН, неравенство 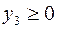должно выполняться как равенство, т. е. 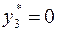. Далее так как 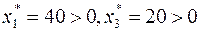, то в силу УДН

.

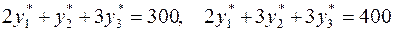Получаем систему линейных уравнений и решаем ее:

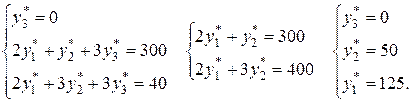
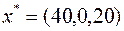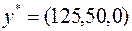Планы и удовлетворяют УДН, следовательно, в силу второй теоремы двойственности, являются оптимальными в задачах (20) и (21) соответственно.

Пример проверки вектора на оптимальность

Исследовать вектор 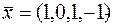на оптимальность в задаче ЛП:

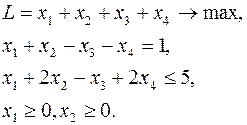
Вначале нужно проверить, является ли вектор 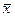допустимым. Для этого подставляем координаты вектора в ограничения:

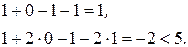
Так как второе ограничение выполняется как строгое неравенство, то в силу УДН для оптимальности вектора 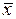необходимо выполнение равенства .

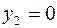Построим двойственную задачу:

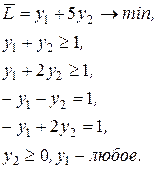
Поскольку 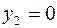, то из третьего и четвертого ограничений получаем 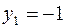. Но по УДН из условия 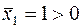следует, что должно выполняться равенство в первом ограничении двойственной задачи:

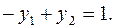
Подставляя значения 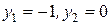, получим 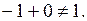Следовательно, УДН не выполняются и вектор 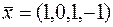не является оптимальным в исходной задаче.

Метод Гомори

Постановка задачи ЦЛП

Задача целочисленного программирования (ЦЛП) формулируется так же, как и задача ЛП, но включается дополнительное требование, состоящее в том, что значения переменных, составляющих оптимальное решение, должны быть целыми неотрицательными числами:

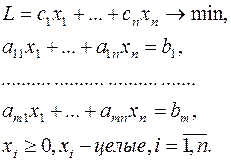(22)

Симплекс-метод не гарантирует целочисленности решения задачи (22), поэтому для отыскания оптимального целочисленного решения задачи ЦЛП требуются специальные методы. Один из таких методов, приводящий к целочисленному решению за конечное число шагов, предложен американским математиком Р. Гомори [1,2]. Идея метода следующая.

С помощью симплекс-метода решается задача ЛП без условия целочисленности. Если оптимальное решение получается нецелочисленным, то вводится дополнительное ограничение, которое, уменьшая многогранник допустимых решений (отсекая некоторую его часть), не исключает из него целочисленных точек. Если оптимальное решение задачи ЛП с дополнительным ограничением целочисленное, то вычисления заканчивают; если же оптимальное решение содержит хотя бы одну дробную компоненту, добавляют новое дополнительное ограничение.

Процесс присоединения дополнительных ограничений повторяют до тех пор, пока либо не будет найдено целочисленное оптимальное решение, либо показано, что задача не имеет целочисленных решений.

Алгоритм метода Гомори

Шаг 1. Симплекс-методом находим оптимальное решение задачи (22) без учета условия целочисленности. Если задача не имеет решения, то неразрешима и исходная задача ЦЛП. В этом случае алгоритм завершает работу.

Шаг 2. Пусть оптимальная таблица имеет вид:

	b		…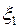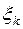
L			…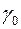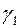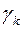
			…
…	…	…………..
			…

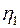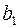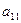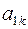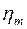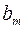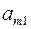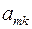Если элементы 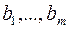– целочисленные, то оптимальное решение 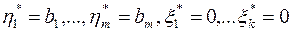является целочисленным. В этом случае вычисления заканчиваем. Иначе, переходим к следующему шагу.

Шаг 3. Среди дробных компонент 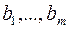таблицы выбираем элемент 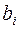с максимальной дробной частью 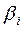и по строке i составляем дополнительное ограничение:

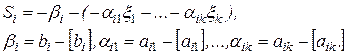
Здесь 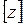– целая часть числа 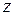(наибольшее целое число, не превышающее число ).

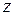Шаг 4. Добавляем построенное ограничение к последней симплекс-таблице и, применяя двойственный симплекс-метод, находим оптимальное решение. Переходим к шагу 2.

Замечания

Признаком отсутствия целочисленного решения служит появление в таблице хотя бы одной строки с дробным свободным членом и целыми остальными коэффициентами (поскольку соответствующее уравнение неразрешимо в целых числах).

На шаге 4 двойственный симплекс-метод применяется до тех пор, пока не будет получена оптимальная симплексная таблица (возможно, потребуется несколько итераций).

Если на шаге 4 в базис вводится переменная дополнительного ограничения 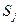, то эта строка вычеркивается из симплексной таблицы (соответствующее ограничение является избыточным).

Пример решения задачи ЦЛП

Решить задачу ЦЛП:

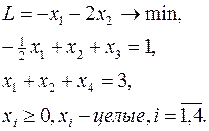
Решаем задачу без условия целочисленности симплекс-методом. Оптимальная таблица имеет вид

	b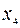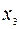
L	-14/3	-4/3	-2/3
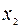	5/3	1/3	2/3
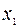	4/3	2/3	-2/3

Оптимальное решение 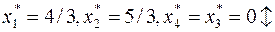не является целочисленным. Выберем среди нецелочисленных переменных переменную с максимальной дробной частью и построим соответствующее отсечение:

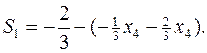
Приписывая это ограничение к симплексной таблице, и проводя стандартное преобразование двойственным симплекс-методом, получим:

	b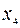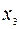
L	-14/3	-4/3	-2/3
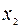	5/3	1/3	2/3
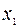	4/3	2/3	-2/3
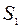	-2/3	-1/3	-2/3

	b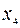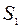
L	-4	-1	-1
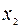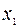			-1
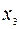		1/2	-3/2

Полученная таблица является оптимальной. Соответствующее оптимальное решение 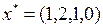является целочисленным. Значение функции на этом решении .

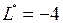Транспортная задача ЛП

Постановка задачи

Классическая транспортная задача ЛП формулируется следующим образом. Имеется m пунктов производства (поставщиков) и n пунктов потребления (потребителей) однородного продукта. Заданы величины:

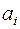- объем производства (запас) i-го поставщика, ;

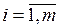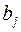- объем потребления (спрос) j-го потребителя,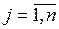

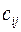- стоимость перевозки (транспортные затраты) единицы продукции от i-го поставщика к j-му потребителю.

Требуется составить такой план перевозок, при котором спрос всех потребителей был бы выполнен, и при этом