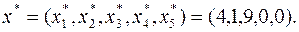Каноническая форма задачи ЛП
Для численного решения задачи ЛП требуется предварительно привести ее к каноническому виду:
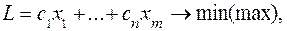
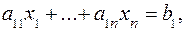 (1)
(1)
………………………
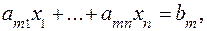
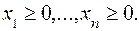
Каноническая форма (КФ) (1) задачи характеризуется следующими тремя признаками:
― однородная система ограничений в виде системы уравнений;
― однородные условия неотрицательности, распространяющиеся на все переменные, участвующие в задаче;
― минимизация (максимизация) целевой функции.
Известно, что для произвольной задачи ЛП можно построить эквивалентную ей каноническую задачу ЛП (эквивалентность двух задач означает, что оптимальному решению одной задачи соответствует оптимальное решение другой)[1,2,3].
Пример построения канонической формы
Привести задачу к КФ на минимум:
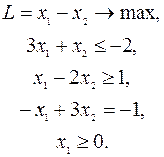 (2)
(2)
В данной задаче (2) нарушены все три признака КФ.
1. Начнем с преобразования смешанной системы ограничений в систему уравнений. Для этого введем в первое и второе ограничения неотрицательные переменные y1, y2, которые называются дополнительными или слабыми. В результате система ограничений запишется в следующем виде:
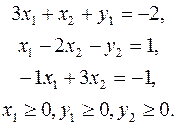 (3)
(3)
2. Условия неотрицательности в (3) не выполняются только для переменной x2. Для приведения задачи к однородным условиям неотрицательности можно воспользоваться двумя приемами.
Первый прием. Представим переменную x2 в виде разности двух неотрицательных переменных: 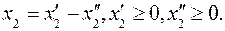 После преобразования системы ограничений и целевой функции получим задачу
После преобразования системы ограничений и целевой функции получим задачу
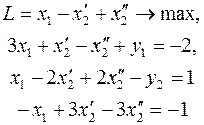 (4)
(4)
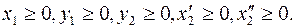
Второй прием. Найдем из какого-либо уравнения (4) переменную x2. Пусть из первого уравнения 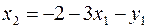 . Подставим это выражение во все уравнения и в целевую функцию, исключив таким образом переменную x2 из задачи. Получим
. Подставим это выражение во все уравнения и в целевую функцию, исключив таким образом переменную x2 из задачи. Получим
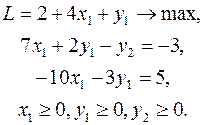 (5)
(5)
3. Переход к задаче минимизации целевой функции L в задаче (5) осуществляется путем введения новой функции 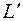 из равенства
из равенства
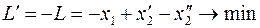 в первом случае,
в первом случае,
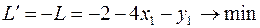 во втором случае.
во втором случае.
1.3. Общие рекомендации к графическому решению задач ЛП
1. Графически могут решаться [1]:
a) задачи, заданные в произвольной форме, содержащие не более двух переменных;
b) задачи, заданные в канонической форме, с числом свободных переменных 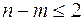 ;
;
c) задачи в произвольной форме записи, которые после приведения к канонической форме будут содержать не более двух свободных переменных 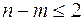 .
.
2. Основной формой для графического решения является 1-й тип задач. Поэтому, если встречается 2-й или 3-й тип задач, то предварительно их модель должна быть приведена к первому типу.
3. Решение задач 1-го типа выполняется в два этапа:
этап 1 – построение области допустимых решений;
этап 2 – построение в допустимой области оптимального решения.
4. При построении области допустимых решений может встретиться один из трех случаев:
а) пустая область – задача не имеет решения из-за несовместности системы ограничений в области допустимых решений;
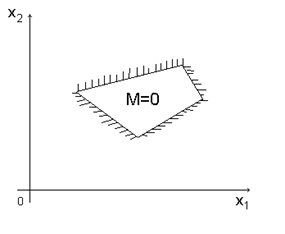
б) выпуклый многоугольник – задача всегда имеет оптимальное решение;
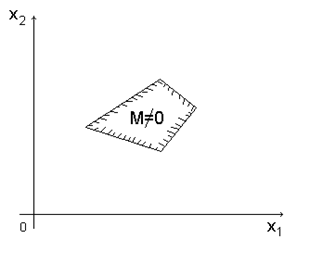
в) неограниченная выпуклая многогранная область – в зависимости от направления вектора c (вектора коэффициентов целевой функции L) задача может иметь или не иметь решение. Последнее связано с неограниченностью целевой функции в области допустимых решений.
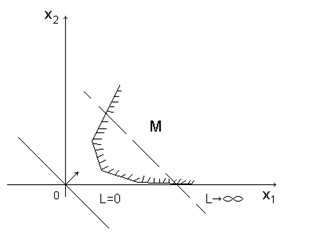
5. Если оптимальное решение существует, то возможен один из трех исходов:
а) оптимальное решение единственное и совпадает с одной из вершин области;
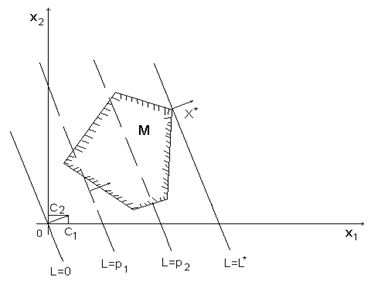
б) оптимальные решения соответствуют всем точкам отрезка, соединяющего две вершины области 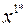 и
и 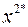 :
: 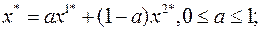
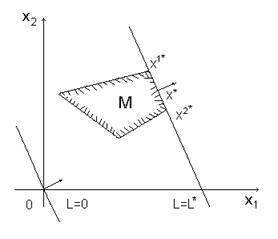
в) оптимальные решения соответствуют всем точкам допустимого луча, исходящего из вершины области 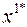 :
: 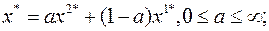
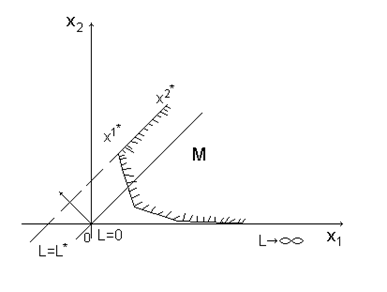
Пример графического решения
Решить графически задачу ЛП, заданную в канонической форме:
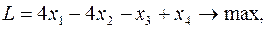 (6)
(6)
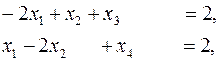
 (7)
(7)
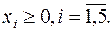 (8)
(8)
Число уравнений задачи m=3, число неизвестных n=5. Тогда n-m=2 и задача может быть сведена к задаче на плоскости относительно свободных переменных. Возьмем в качестве базисных переменные 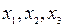 и выразим их через свободные (небазисные переменные):
и выразим их через свободные (небазисные переменные):
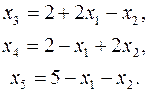 (9)
(9)
По условию (8) переменные могут принимать только неотрицательные значения, т. е. допустимой областью задачи ЛП (6) - (8) будет область, определяемая условиями (8), (9), или
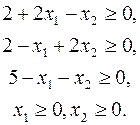 (10)
(10)
Чтобы получить задачу ЛП относительно переменных 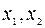 , подставим значения базисных переменных (9) в целевую функцию (6). В результате получим
, подставим значения базисных переменных (9) в целевую функцию (6). В результате получим
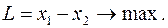 (11)
(11)
Задача (10), (11) эквивалентна задаче (6) - (8), поэтому решая графически задачу (10), (11), получим решение задачи (6) - (8).
Этап 1. Построение допустимой области.
Каждое из неравенств (10) определяет некоторую полуплоскость 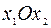 :
:
Так, неравенство 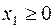 определяет правую полуплоскость. Неравенство
определяет правую полуплоскость. Неравенство 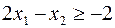 определяет полуплоскость, лежащую по ту сторону от прямой
определяет полуплоскость, лежащую по ту сторону от прямой 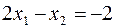 , где
, где 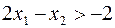 . Подставляя значения
. Подставляя значения 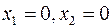 в это неравенство, получим 0>-2, значит, координаты (0,0) удовлетворяют первому неравенству (10) и область решений этого неравенства включает начало координат. Аналогично определяют полуплоскости остальных неравенств (10).
в это неравенство, получим 0>-2, значит, координаты (0,0) удовлетворяют первому неравенству (10) и область решений этого неравенства включает начало координат. Аналогично определяют полуплоскости остальных неравенств (10).
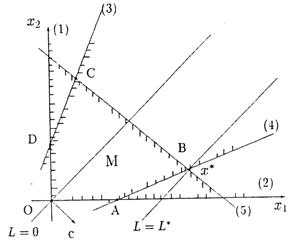
На рисунке прямые, соответствующие условию 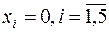 , отмечены цифрой в скобках.
, отмечены цифрой в скобках.
Получили допустимую область M – выпуклый пятиугольник OABCD.
Этап 2. В допустимой области M находим оптимальное решение.
Строим прямую 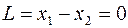 и определяем направление возрастания функции
и определяем направление возрастания функции 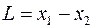 , это направление вектора
, это направление вектора 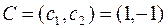 . Перемещая прямую L параллельно самой себе в направлении вектора
. Перемещая прямую L параллельно самой себе в направлении вектора 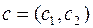 до тех пор, пока она будет сохранять общие точки с областью допустимых решений, найдем, что в крайнем возможном положении прямая L пройдет через точку
до тех пор, пока она будет сохранять общие точки с областью допустимых решений, найдем, что в крайнем возможном положении прямая L пройдет через точку 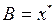 . Этому положению прямой L соответствует значение
. Этому положению прямой L соответствует значение 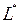 . Для нахождения координат точки
. Для нахождения координат точки 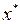 необходимо совместно решить систему уравнений граничных прямых, на которых лежит точка
необходимо совместно решить систему уравнений граничных прямых, на которых лежит точка 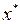 :
:
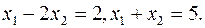
В результате получаем искомое оптимальное решение 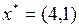 . Подставляя значения
. Подставляя значения 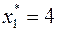 и
и 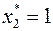 в целевую функцию и в равенства (9), получим оптимальное значение целевой функции
в целевую функцию и в равенства (9), получим оптимальное значение целевой функции 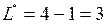 и оптимальное решение:
и оптимальное решение: