Симплекс метод (минимум)
Симплекс метод - универсальный метод для решения линейной системы уравнений или неравенств и линейного функционала.
Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП (задачи линейного программирования) состоит
- умение находить начальный опорный план;
- наличие признака оптимальности опорного плана;
- умение переходить к нехудшему опорному плану.
Пусть ЗЛП представлена системой ограничений в каноническом виде:
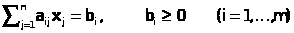 .
.
Говорят, что ограничение ЗЛП имеет предпочтительный вид, если при неотрицательной правой части 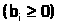 левая часть ограничений содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения равенства - с коэффициентом, равным нулю.
левая часть ограничений содержит переменную, входящую с коэффициентом, равным единице, а в остальные ограничения равенства - с коэффициентом, равным нулю.
Пусть система ограничений имеет вид
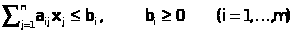
Сведем задачу к каноническому виду. Для этого прибавим к левым частям неравенств дополнительные переменные 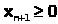
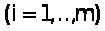 . Получим систему, эквивалентную исходной:
. Получим систему, эквивалентную исходной:
 ,
,
которая имеет предпочтительный вид
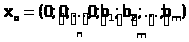 .
.
В целевую функцию дополнительные переменные вводятся с коэффициентами, равными нулю 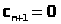
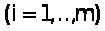 .
.
Пусть далее система ограничений имеет вид
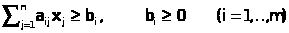
Сведём её к эквивалентной вычитанием дополнительных переменных 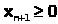
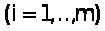 из левых частей неравенств системы. Получим систему
из левых частей неравенств системы. Получим систему

Однако теперь система ограничений не имеет предпочтительного вида, так как дополнительные переменные 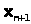 входят в левую часть (при
входят в левую часть (при 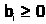 ) с коэффициентами, равными –1. Поэтому, вообще говоря, базисный план
) с коэффициентами, равными –1. Поэтому, вообще говоря, базисный план 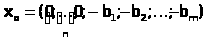 не является допустимым. В этом случае вводится так называемый искусственный базис. К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные
не является допустимым. В этом случае вводится так называемый искусственный базис. К левым частям ограничений-равенств, не имеющих предпочтительного вида, добавляют искусственные переменные 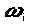 . В целевую функцию переменные
. В целевую функцию переменные 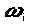 , вводят с коэффициентом М в случае решения задачи на минимум и с коэффициентом -М для задачи на максимум, где М - большое положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.
, вводят с коэффициентом М в случае решения задачи на минимум и с коэффициентом -М для задачи на максимум, где М - большое положительное число. Полученная задача называется М-задачей, соответствующей исходной. Она всегда имеет предпочтительный вид.
Пусть исходная ЗЛП имеет вид
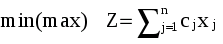 (1)
(1)
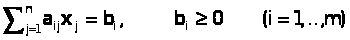 (2)
(2)
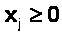
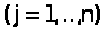 (3)
(3)
причём ни одно из ограничений не имеет предпочтительной переменной. М-задача запишется так:
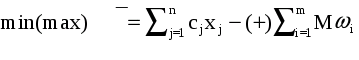
Z
(4)
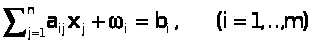 (5)
(5)
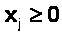
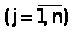 ,
, 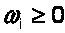 ,
, 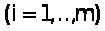 (6)
(6)
Задача (4)-(6) имеет предпочтительный план. Её начальный опорный план имеет вид
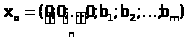
Если некоторые из уравнений (2) имеют предпочтительный вид, то в них не следует вводить искусственные переменные.
Теорема. Если в оптимальном плане
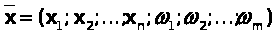 (7)
(7)
М-задачи (4)-(6) все искусственные переменные 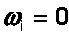
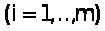 , то план
, то план 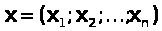 является оптимальным планом исходной задачи (1)-(3).
является оптимальным планом исходной задачи (1)-(3).
Для того чтобы решить задачу с ограничениями, не имеющими предпочтительного вида, вводят искусственный базис и решают расширенную М-задачу, которая имеет начальный опорный план 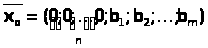
Решение исходной задачи симплексным методом путем введения искусственных переменных 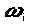 называется симплексным методом с искусственным базисом.
называется симплексным методом с искусственным базисом.
Если в результате применения симплексного метода к расширенной задаче получен оптимальный план, в котором все искусственные переменные 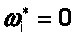 , то его первые n компоненты дают оптимальный план исходной задачи.
, то его первые n компоненты дают оптимальный план исходной задачи.
Теорема. Если в оптимальном плане М-задачи хотя бы одна из искусственных переменных отлична от нуля, то исходная задача не имеет допустимых планов, т. е. ее условия несовместны.
Признаки оптимальности.
Теорема. Пусть исходная задача решается на максимум. Если для некоторого опорного плана все оценки 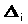
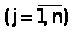 неотрицательны, то такой план оптимален.
неотрицательны, то такой план оптимален.
Теорема. Если исходная задача решается на минимум и для некоторого опорного плана все оценки 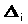
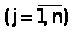 неположительны, то такой план оптимален.
неположительны, то такой план оптимален.
Для привидения системы ограничений неравенств к каноническому виду, необходимо в системе ограничений выделить единичный базис.
