Алгоритм симплекс метода

Начальный этап. Пусть e> 0 - скаляр, используемый в критерии остановки, l – длина ребра симплекса, α – коэффициент уменьшения размеров симплекса. Выбрать начальную точку X₁, рассчитать вершины исходного симплекса X₁, X₂, …, Х_n+1, определить значение функции в этих вершинах f(X₁),…, f(X_n+1) и перейти к основному этапу.

Основной этап. Шаг 1. Определить из n+1 вершин вершину с максимальным значением функции и соответствующий ей номер j. Рассчитать новую вершину Х_n+2= 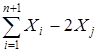. Если f(X_n+2)≤ f(X_j), то X_j=X_n+2 и перейти к шагу 1. В противном случае перейти к шагу 2.

Шаг 2. Если длина ребра 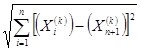£ e, то остановиться; в противном случае провести редукцию симплекса. Выбрать из n+1 вершин вершину с минимальным значением функции и соответствующий ей номер m. Рассчитать вершины нового симплекса X_i= ((1- α )X_m + Xi)/α для i ≠m, вычислить значения функции f(X₁),…, f(X_n+1) и перейти к шагу 1.

Пример расчета экстремума функции симплекс-методом.

Постановка задачи. Минимизировать f(X) = (x₁ - 2)⁴ + (х₁ - 2х₂)² с точностью e=0,01. Выбираем начальное приближение X⁽¹⁾ = [2.5, 2.5]^Т, длину ребра симплекса l=0.5 и коэффициент сжатия симплекса a = 2.

Результаты расчета для данных условий представлены в таблице 2.4, графическая интерпретация метода – на рисунке 2.4.

Таблица 2.4

Результаты расчета минимума функции f(X) = (x₁ - 2)⁴ + (х₁ - 2х₂)² симплекс методом.

№	№ вершины	x1	x2	f(X)	№	№ вершины	x1	x2	f(X)
		2.250	2.360	6.1048			2.500	1.520	0.3541
	2.500	2.780	9.4261		2.625	1.310	0.1526
	2.750	2.360	4.1973		2.750	1.520	0.4005
		2.250	2.360	6.1048			2.500	1.520	0.3541
	2.500	1.940	1.9669		2.625	1.310	0.1526
	2.750	2.360	4.1973		2.375	1.310	0.0798
		3.000	1.940	1.7744			2.500	1.100	0.1525
	2.500	1.940	1.9669		2.625	1.310	0.1526
	2.750	2.360	4.1973		2.375	1.310	0.0798
		3.000	1.940	1.7744			2.500	1.100	0.1525
	2.500	1.940	1.9669		2.250	1.100	0.0064
	2.750	1.520	0.4005		2.375	1.310	0.0798
		3.000	1.940	1.7744			2.125	1.310	0.2453
	3.250	1.520	2.4855		2.250	1.100	0.0064
	2.750	1.520	0.4005		2.375	1.31	0.0798
Редукция симплекса	Редукция симплекса
		2.88	1.730	0.9284			2.188	1.205	0.0507
	2.63	1.730	0.8498		2.313	1.205	0.0190
	2.75	1.520	0.4005		2.375	1.310	0.0798
		2.50	1.520	0.3541
	2.63	1.730	0.8498
	2.75	1.520	0.4005

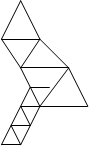
Из таблицы видно, что на пятой итерации происходит зацикливание симплекса, так как отраженная вершина № 2 вновь становится «наихудшей». После редукции симплекса реализовано семь итераций, после чего вновь появляется эффект зацикливания. В результате чего вновь производится редукция. Полученный симплекс не находится в области экстремума функции. Поэтому проведенная редукция не дает желаемого результата, что говорит о плохой сходимости метода на функциях "овражного" типа.

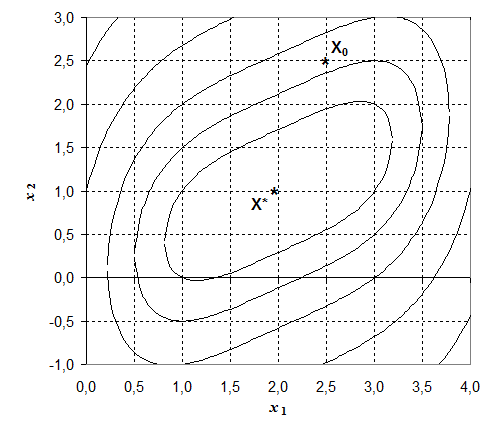Рис.2.4. Графическая иллюстрация поиска минимума функции симплекс-методом.

Метод Нелдера и Мида.

Отмеченные выше недостатки регулярного симплекса, а также отсутствие ускорения поиска и трудности при проведении поиска на искривленных “оврагах” и “хребтах” явились причиной разработки Нелдером и Мидом метода, в котором симплекс меняет свою форму, т. е. представляет деформируемый многогранник. Изменение формы многогранника происходит за счет операций растяжения, сжатия и редукции.

1. Построение начального многогранника. Выбирается произвольной формы многогранник с координатами вершин

X_i^(k) = [x_i1^(k), …, x_ij^(k), …, x_in^(k)]^Т, i = 1,…, n+1.

Индекс (k) будет обозначать k-й этап поиска. Значение целевой функции в X_i^(k) равно f(X_i^(k)).

2. Расчет координат центра тяжести. Определяют те векторы х многогранника, которые дают максимальное и минимальное значение f(X), а именно

f(X_h^(k)) = max{f(X₁^(k)), …, f(X_n+1^(k)); f(X_l^(k)) = min{ f(X₁^(k)), …, f(X_n+1^(k)).

Тогда координаты центра тяжести рассчитываются по формуле

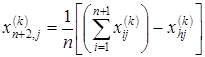, j = 1, …, n,

где индекс j обозначает координатное направление.

3. Отражение. Представляет проектирование X_h^(k) через центр тяжести в соответствии с соотношением

,

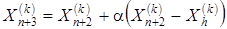где a > 0 - коэффициент отражения;

X_h^(k) - вершина, в которой функция f(X) имеет наибольшее значение.

В обычном симплексе a = 1.

4. Растяжение. Происходит в случае, если 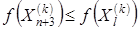. Вектор ( 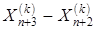) увеличивается в соответствии с соотношением

,

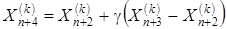где g > 1 - коэффициент растяжения.

Если 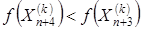, то 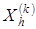заменяется на 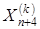и процедура продолжается с этапа 2 при k = k + 1. Иначе 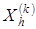заменяется на 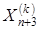и также осуществляется переход к этапу 2 при k = k + 1.

5. Сжатие. Если 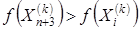для всех i ¹ h, то вектор ( 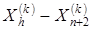) уменьшается в соответствии с формулой

,

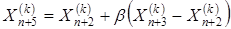где 0 < b < 1 - коэффициентом сжатия.

Затем 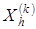заменить на 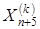и происходит возврат к операции 2 при k = k + 1.

6. Редукция. Происходит при условии, если 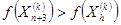. Все векторы ( 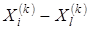) уменьшаются в 2 раза с отсчетом от 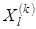в соответствии с формулой

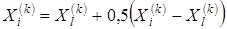, i=1, …, n+1.

Затем возвращаемся к операции 2 для продолжения поиска на (k+1)-м шаге.

Для окончания поиска Нилдер и Мид используют критерий вида

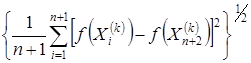£ e ,

где e- заданная точность поиска;

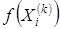- значение функции в центре тяжести.