Графическое решение задач ЛП
А.В. Зыкина
МЕТОДЫ ОПТИМИЗАЦИИ
Конспект лекций
Омск 2007
УДК 007(075)
ББК 32.81я73
З-96
Рецензенты:
О.В. Кириченова, канд. физ.-мат. наук, доц. ОмГПУ;
О.П. Диденко, канд. пед. наук, доц. ОмГИС
Зыкина, А.В.
З-96 Методы оптимизации: конспект лекций /А.В. Зыкина. – Омск: Изд-во
ОмГТУ, 2007. – 36 с.
В конспекте лекций приводятся основные теоретические сведения по линейной оптимизации. Излагается графический метод решения задачи линейного программирования, рассматриваются прямой и двойственный симплекс-методы, метод отсечений для задачи целочисленной оптимизации, метод потенциалов для решения транспортной задачи линейного программирования.
Конспект лекций предназначен для студентов специальности 230102 и направления подготовки 23010062.
Печатается по решению редакционно-издательского совета Омского государственного технического университета.
УДК 007(075)
ББК 32.81я73
Редактор Н.Н. Пацула
ИД № 06039 от 12,10,2001
Сводный темплан 2007 г.
Подписано к печати 20.02.07. Бумага офсетная.
Формат 60´84 1/16. Отпечатано на дупликаторе.
Усл. печ. л. 2,25. Уч.-изд. л. 2,25
Тираж . экз. Заказ
Издательство ОмГТУ. 644050, г. Омск, пр-т Мира,11
Типография ОмГТУ
© А.В. Зыкина, 2007
© Омский государственный
технический университет, 2007
Введение
При решении широкого комплекса практических задач, в том числе задач создания и эксплуатации АСОИУ, возникают своеобразные модели оптимизации решений, для которых характерны следующие черты:
1) показатель эффективности (целевая функция) является линейной функцией от элементов решения;
2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств.
Такие задачи называются задачами линейного программирования (ЛП).
Первые исследования по ЛП были проведены в конце 30-х годов в Ленинградском университете академиком Л. В. Кантаровичем (первая публикация – в 1939 году). Л. В. Кантарович предложил легко алгоритмизируемый метод решения задач ЛП – метод последовательного улучшения допустимого вектора. Американский математик Дж. Данциг в 1947 году разработал симплекс-метод решения задачи ЛП. По существу симплекс-метод является табличной формой записи метода последовательного улучшения допустимого вектора. В 1951 году Дж. Данциг ввел термин «линейное программирование» (слово «программирование» в данном случае означает не что иное, как «планирование»).
В настоящее время, с точки зрения уровня теоретических разработок, сфера приложения и реализации вычислительных методов ЛП является одним из наиболее развитых направлений в области решения оптимизационных задач. Успехи в использовании методов ЛП во многом обусловлены значительным увеличением быстродействия и объема памяти ЭВМ. Достижения в области ЛП в свою очередь содействовали прогрессу в разработке алгоритмов решения других задач математического программирования. Сущность этих алгоритмов состоит в том, что исходная (в общем случае, нелинейная) задача сводится к одной линейной задаче или их совокупности. Таким образом, линейное программирование выделяется среди других методов программирования как основа для многих процедур решения.
При нахождении решений для моделей математического программирования (МП) применительно к реальным задачам процедуры ручного счета практически никогда не используются. Такого рода работа, как правило, осуществляется с помощью ЭВМ. Возникает вполне законный вопрос: не достаточно ли одного умения строить модели? Нет, не достаточно. Значительный опыт по использованию методов математического программирования при решении производственных задач подтвердил, что руководитель должен понимать принцип работы алгоритмов, чтобы добиться действительно эффективного и обоснованного применения этого инструмента организации управления. При практическом применении МП всегда стремятся получить более содержательную информацию, нежели ответ в числовом выражении. Главная цель расчетов – не цифры, а понимание.
Графическое решение задач ЛП
Пример построения канонической формы
Привести задачу к КФ на минимум:
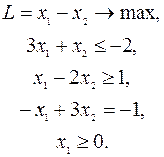 (2)
(2)
В данной задаче (2) нарушены все три признака КФ.
1. Начнем с преобразования смешанной системы ограничений в систему уравнений. Для этого введем в первое и второе ограничения неотрицательные переменные y1, y2, которые называются дополнительными или слабыми. В результате система ограничений запишется в следующем виде:
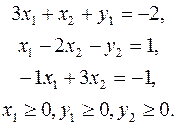 (3)
(3)
2. Условия неотрицательности в (3) не выполняются только для переменной x2. Для приведения задачи к однородным условиям неотрицательности можно воспользоваться двумя приемами.
Первый прием. Представим переменную x2 в виде разности двух неотрицательных переменных: 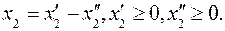 После преобразования системы ограничений и целевой функции получим задачу
После преобразования системы ограничений и целевой функции получим задачу
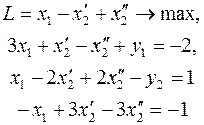 (4)
(4)
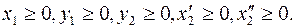
Второй прием. Найдем из какого-либо уравнения (4) переменную x2. Пусть из первого уравнения 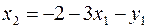 . Подставим это выражение во все уравнения и в целевую функцию, исключив таким образом переменную x2 из задачи. Получим
. Подставим это выражение во все уравнения и в целевую функцию, исключив таким образом переменную x2 из задачи. Получим
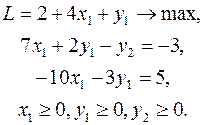 (5)
(5)
3. Переход к задаче минимизации целевой функции L в задаче (5) осуществляется путем введения новой функции 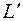 из равенства
из равенства
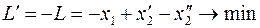 в первом случае,
в первом случае,
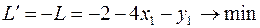 во втором случае.
во втором случае.
1.3. Общие рекомендации к графическому решению задач ЛП
1. Графически могут решаться [1]:
a) задачи, заданные в произвольной форме, содержащие не более двух переменных;
b) задачи, заданные в канонической форме, с числом свободных переменных 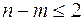 ;
;
c) задачи в произвольной форме записи, которые после приведения к канонической форме будут содержать не более двух свободных переменных 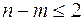 .
.
2. Основной формой для графического решения является 1-й тип задач. Поэтому, если встречается 2-й или 3-й тип задач, то предварительно их модель должна быть приведена к первому типу.
3. Решение задач 1-го типа выполняется в два этапа:
этап 1 – построение области допустимых решений;
этап 2 – построение в допустимой области оптимального решения.
4. При построении области допустимых решений может встретиться один из трех случаев:
а) пустая область – задача не имеет решения из-за несовместности системы ограничений в области допустимых решений;
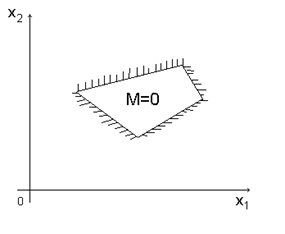
б) выпуклый многоугольник – задача всегда имеет оптимальное решение;
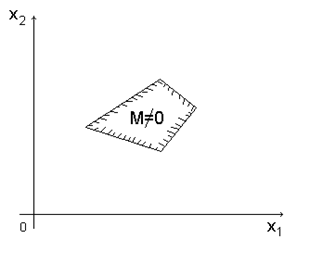
в) неограниченная выпуклая многогранная область – в зависимости от направления вектора c (вектора коэффициентов целевой функции L) задача может иметь или не иметь решение. Последнее связано с неограниченностью целевой функции в области допустимых решений.
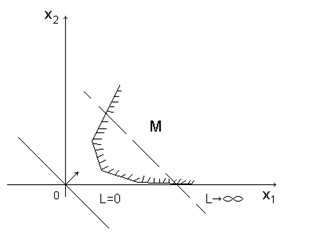
5. Если оптимальное решение существует, то возможен один из трех исходов:
а) оптимальное решение единственное и совпадает с одной из вершин области;
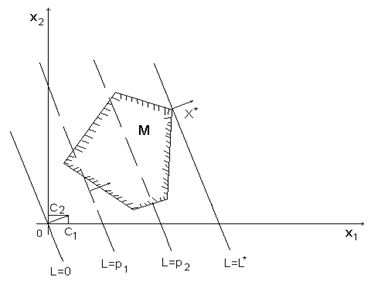
б) оптимальные решения соответствуют всем точкам отрезка, соединяющего две вершины области 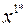 и
и 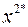 :
: 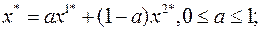
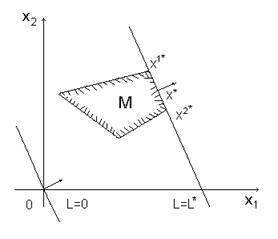
в) оптимальные решения соответствуют всем точкам допустимого луча, исходящего из вершины области 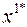 :
: 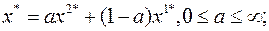
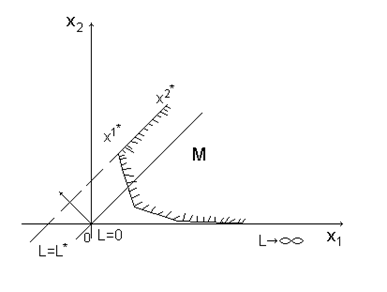
Пример графического решения
Решить графически задачу ЛП, заданную в канонической форме:
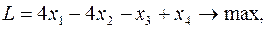 (6)
(6)
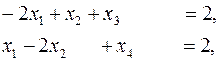
 (7)
(7)
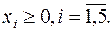 (8)
(8)
Число уравнений задачи m=3, число неизвестных n=5. Тогда n-m=2 и задача может быть сведена к задаче на плоскости относительно свободных переменных. Возьмем в качестве базисных переменные 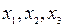 и выразим их через свободные (небазисные переменные):
и выразим их через свободные (небазисные переменные):
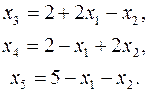 (9)
(9)
По условию (8) переменные могут принимать только неотрицательные значения, т. е. допустимой областью задачи ЛП (6) - (8) будет область, определяемая условиями (8), (9), или
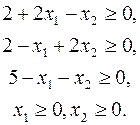 (10)
(10)
Чтобы получить задачу ЛП относительно переменных 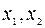 , подставим значения базисных переменных (9) в целевую функцию (6). В результате получим
, подставим значения базисных переменных (9) в целевую функцию (6). В результате получим
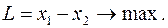 (11)
(11)
Задача (10), (11) эквивалентна задаче (6) - (8), поэтому решая графически задачу (10), (11), получим решение задачи (6) - (8).
Этап 1. Построение допустимой области.
Каждое из неравенств (10) определяет некоторую полуплоскость 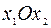 :
:
Так, неравенство 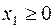 определяет правую полуплоскость. Неравенство
определяет правую полуплоскость. Неравенство 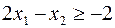 определяет полуплоскость, лежащую по ту сторону от прямой
определяет полуплоскость, лежащую по ту сторону от прямой 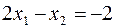 , где
, где 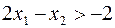 . Подставляя значения
. Подставляя значения 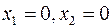 в это неравенство, получим 0>-2, значит, координаты (0,0) удовлетворяют первому неравенству (10) и область решений этого неравенства включает начало координат. Аналогично определяют полуплоскости остальных неравенств (10).
в это неравенство, получим 0>-2, значит, координаты (0,0) удовлетворяют первому неравенству (10) и область решений этого неравенства включает начало координат. Аналогично определяют полуплоскости остальных неравенств (10).
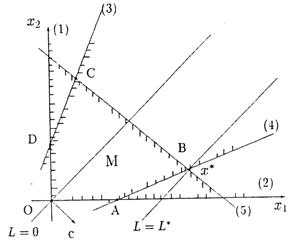
На рисунке прямые, соответствующие условию 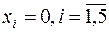 , отмечены цифрой в скобках.
, отмечены цифрой в скобках.
Получили допустимую область M – выпуклый пятиугольник OABCD.
Этап 2. В допустимой области M находим оптимальное решение.
Строим прямую 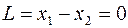 и определяем направление возрастания функции
и определяем направление возрастания функции 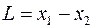 , это направление вектора
, это направление вектора 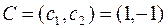 . Перемещая прямую L параллельно самой себе в направлении вектора
. Перемещая прямую L параллельно самой себе в направлении вектора 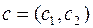 до тех пор, пока она будет сохранять общие точки с областью допустимых решений, найдем, что в крайнем возможном положении прямая L пройдет через точку
до тех пор, пока она будет сохранять общие точки с областью допустимых решений, найдем, что в крайнем возможном положении прямая L пройдет через точку 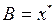 . Этому положению прямой L соответствует значение
. Этому положению прямой L соответствует значение 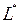 . Для нахождения координат точки
. Для нахождения координат точки 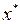 необходимо совместно решить систему уравнений граничных прямых, на которых лежит точка
необходимо совместно решить систему уравнений граничных прямых, на которых лежит точка 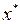 :
:
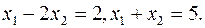
В результате получаем искомое оптимальное решение 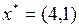 . Подставляя значения
. Подставляя значения 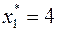 и
и 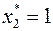 в целевую функцию и в равенства (9), получим оптимальное значение целевой функции
в целевую функцию и в равенства (9), получим оптимальное значение целевой функции 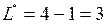 и оптимальное решение:
и оптимальное решение: 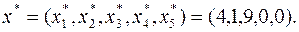
Симплекс-метод
Рассмотрим задачу ЛП в канонической форме:
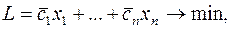 (12)
(12)
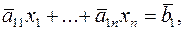
……………………… (13)
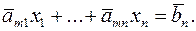
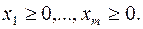 (14)
(14)
Будем предполагать, что 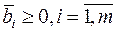 (иначе, умножим соответствующее уравнение на -1, уравнения системы (13) линейно независимы, m<n и система (13) - (14) совместна.
(иначе, умножим соответствующее уравнение на -1, уравнения системы (13) линейно независимы, m<n и система (13) - (14) совместна.
При сделанных предположениях можно выбрать m неизвестных (к примеру 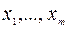 ) таких, чтобы определитель, составленный из коэффициентов при этих неизвестных, не обращался в ноль. Тогда задача (12) - (14) может быть приведена к виду, который называется специальной формой задачи ЛП:
) таких, чтобы определитель, составленный из коэффициентов при этих неизвестных, не обращался в ноль. Тогда задача (12) - (14) может быть приведена к виду, который называется специальной формой задачи ЛП:
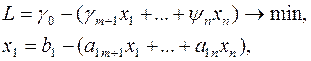
…………………………………….. (15)
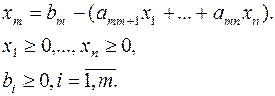
Одно из допустимых решений этой задачи можно найти, если переменные 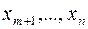 положить равными нулю. Такое решение называется допустимым базисным решением. Оно имеет вид
положить равными нулю. Такое решение называется допустимым базисным решением. Оно имеет вид
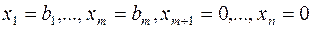 .
.
Этому решению соответствует значение целевой функции 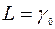 . Переменные
. Переменные 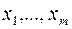 называют базисными, набор переменных
называют базисными, набор переменных 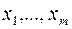 называют базисом, а переменные
называют базисом, а переменные 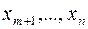 называют небазисными или свободными. Число возможных базисов в задаче размерности n с m ограничениями не превосходит величину
называют небазисными или свободными. Число возможных базисов в задаче размерности n с m ограничениями не превосходит величину 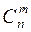 .
.
Известно, что каждому допустимому базисному решению соответствует вершина многоугольника допустимых решений и оптимальное решение задачи (при условии его существования) достигается в одной из вершин многоугольника. Поэтому оптимальное решение задачи ЛП находится среди допустимых базисных решений. Существуют рациональные способы последовательного перебора допустимых базисных решений, которые позволяют рассматривать не все допустимые базисные решения, а их минимальное число. К таким методам относится симплекс-метод [1,2,3].
Пример решения задачи симплекс-методом
Решить задачу, записанную в виде (15).
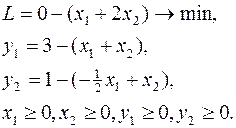
Составим симплексную таблицу:
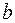 | 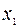 | 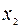 | |
| L | |||
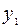 | |||
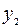 | 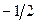 |
Так как коэффициенты строки целевой функции неотрицательны, то начальное базисное решение 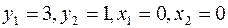 не является оптимальным. Значение целевой функции для этого базиса L=0.
не является оптимальным. Значение целевой функции для этого базиса L=0.
Выбираем ведущий столбец – это столбец, соответствующий переменной 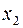 .
.
Выбираем ведущую строку. Для этого находим 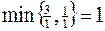 . Следовательно, ведущая строка соответствует переменной
. Следовательно, ведущая строка соответствует переменной 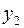 .
.
Проводим преобразование симплексной таблицы, вводя переменную 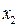 в базис и выводя переменную
в базис и выводя переменную 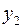 из базиса. Получим таблицу:
из базиса. Получим таблицу:
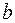 | 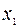 | 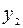 | |
| L | -2 | -2 | |
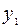 | 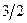 | -1 | |
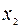 | 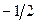 |
Одна итерация метода завершена. Переходим к новой итерации. Полученная таблица неоптимальная. Базисное решение, соответствующее таблице, имеет вид 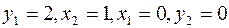 . Значение целевой функции на этом базисе L= -2.
. Значение целевой функции на этом базисе L= -2.
Ведущий столбец здесь – столбец, соответствующий переменной 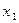 . Ведущая строка – строка, соответствующая переменной
. Ведущая строка – строка, соответствующая переменной 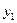 . После проведения преобразований получим симплексную таблицу:
. После проведения преобразований получим симплексную таблицу:
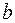 | 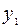 | 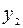 | |
| L | 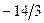 | 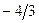 | 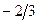 |
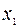 | 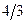 | 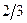 | 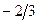 |
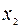 | 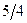 | 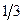 | 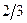 |
Еще одна итерация завершена. Переходим к новой итерации.
Строка целевой функции не содержит положительных значений, значит, соответствующее базисное решение 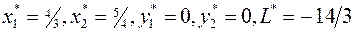 является оптимальным, и алгоритм завершает работу.
является оптимальным, и алгоритм завершает работу.
Метод искусственного базиса
Симплекс-метод применяется для решения задач ЛП, представленных в специальной форме:
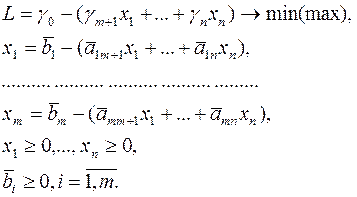 (16)
(16)
Характерная особенность задачи (16) – известное базисное допустимое решение
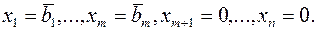
Чтобы применить симплекс-метод для решения задачи ЛП в произвольной форме, необходимо привести эту задачу к виду (16), т. е. выделить начальное допустимое базисное решение. Для этого в симплекс-метод вводят подготовительный этап. Один из методов для реализации подготовительного этапа называется методом искусственного базиса и состоит в следующем [1,2,3].
Вычислительная схема метода искусственного базиса
Шаг 1. Приводим задачу ЛП к канонической форме с неотрицательными правыми частями 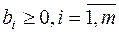 :
:
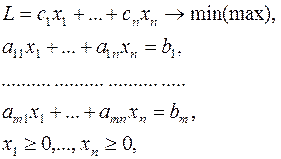 (17)
(17)
Шаг 2. В каждую i-ю строку ограничений (17) вводим искусственную неотрицательную переменную 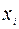 и строим вспомогательную задачу ЛП вида:
и строим вспомогательную задачу ЛП вида:
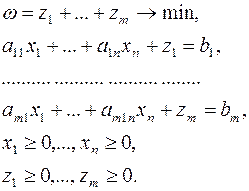 (18)
(18)
В задаче (18) 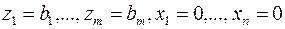 – допустимое базисное решение, и задача (18) легко может быть сведена к виду (16). Для этого целевую функцию необходимо выразить через свободные переменные
– допустимое базисное решение, и задача (18) легко может быть сведена к виду (16). Для этого целевую функцию необходимо выразить через свободные переменные 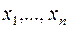 :
:
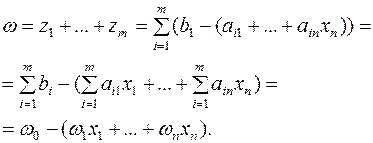
Шаг 3. Для вспомогательной задачи (18) строим симплексную таблицу
| b | 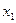 | … | 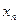 | |
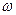 | 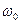 | 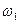 | … | 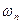 |
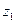 | 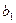 | 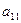 | … | 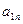 |
| … | … | …………………. | ||
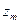 | 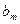 | 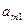 | … | 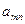 |
и находим оптимальное решение вспомогательной задачи с помощью симплекс-метода.
Шаг 4. Если 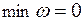 и все переменные
и все переменные 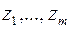 являются небазисными, то m переменных из
являются небазисными, то m переменных из 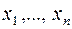 войдут в базис и система ограничений, соответствующих симплексной таблице, будет иметь вид
войдут в базис и система ограничений, соответствующих симплексной таблице, будет иметь вид
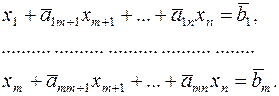 (19)
(19)
Так как переменные 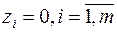 , то их исключили из системы (19), не нарушив при этом равенств. Выражая целевую функцию основной задачи
, то их исключили из системы (19), не нарушив при этом равенств. Выражая целевую функцию основной задачи 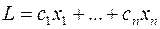 через небазисные переменные
через небазисные переменные 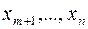 системы (19), получим исходную задачу (17) в виде (16).
системы (19), получим исходную задачу (17) в виде (16).
Шаг 5. Если 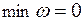 , но в базисе остались искусственные переменные
, но в базисе остались искусственные переменные 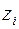 , для которых
, для которых 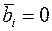 (вырожденный случай), то проводим для каждой искусственной переменной
(вырожденный случай), то проводим для каждой искусственной переменной 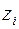 из базиса следующее преобразование симплексной таблицы.
из базиса следующее преобразование симплексной таблицы.
Выбираем ведущим столбцом столбец такой переменной 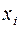 , для которой элемент индексной строки
, для которой элемент индексной строки 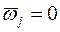 , а элемент столбца
, а элемент столбца 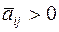 . В этом случае строка искусственной переменной
. В этом случае строка искусственной переменной 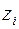 будет ведущей и после стандартного преобразования симплексной таблицы (шаг 6 из прямого симплекс-метода) искусственная переменная
будет ведущей и после стандартного преобразования симплексной таблицы (шаг 6 из прямого симплекс-метода) искусственная переменная 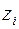 выведется из базиса. В результате получим симплексную таблицу, соответствующую шагу 4.
выведется из базиса. В результате получим симплексную таблицу, соответствующую шагу 4.
Шаг 6. Если 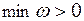 , то допустимого решения в исходной задаче (17) не существует (не могут все искусственные переменные
, то допустимого решения в исходной задаче (17) не существует (не могут все искусственные переменные 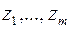 быть равными нулю в задаче (18), а значит система ограничений задачи (17) несовместна) – процесс решения исходной задачи (17) завершается.
быть равными нулю в задаче (18), а значит система ограничений задачи (17) несовместна) – процесс решения исходной задачи (17) завершается.
Пример решения задачи методом искусственного базиса
Выделить допустимое базисное решение для задачи ЛП:
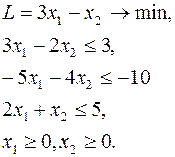
Приведем задачу к канонической форме на минимум с неотрицательными правыми частями:
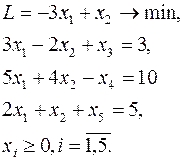
Заметим, что переменные 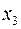 и
и 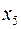 можно использовать для введения в исходный базис, поэтому в первую и третью строку ограничений можно не вводить искусственные переменные.
можно использовать для введения в исходный базис, поэтому в первую и третью строку ограничений можно не вводить искусственные переменные.
Во вторую строку ограничений вводим искусственную переменную z, потому что в этой строке нет переменной, которую можно взять базисной, не проводя при этом дополнительных преобразований всей системы ограничений.
Полученная вспомогательная задача имеет вид
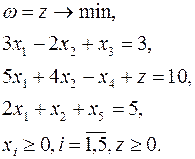
Приведем задачу к виду (16):
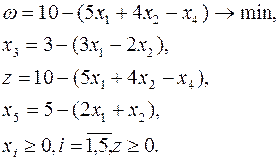
Выпишем соответствующую симплексную таблицу:
| B | 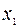 | 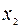 | 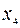 | |
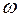 | -1 | |||
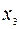 | -2 | |||
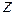 | -1 | |||
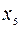 |
Ведущий столбец рекомендуется выбирать не по максимальному положительному элементу строки целевой функции, а так, чтобы из базиса выводилась искусственная базисная переменная (соответствующая ведущая строка должна быть строкой искусственной переменной). Так, выбрав ведущим столбцом столбец переменной 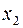 , получим ведущую строку – строку с переменной z (выбирая ведущим столбцом
, получим ведущую строку – строку с переменной z (выбирая ведущим столбцом 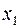 , получили бы ведущую строку
, получили бы ведущую строку 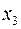 , и из базиса выводилась бы переменная
, и из базиса выводилась бы переменная 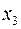 ).
).
Итак, искусственная переменная z выйдет из базиса, а переменная 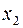 введется в базис.
введется в базис.
Симплексная таблица преобразуется к виду:
| B | 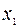 | 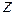 | 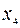 | |
 | -1 | |||
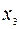 | 11/2 | 1/2 | -1/2 | |
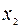 | 5/2 | 5/4 | 1/4 | -1/4 |
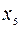 | 5/2 | 3/4 | -1/4 | 1/4 |
Так как значение 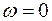 , то полученный базис
, то полученный базис 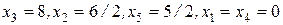 является начальным допустимым базисом для исходной задачи ЛП. Чтобы выразить целевую функцию
является начальным допустимым базисом для исходной задачи ЛП. Чтобы выразить целевую функцию 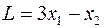 через небазисные переменные
через небазисные переменные 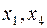 , подставим значение базисной переменной
, подставим значение базисной переменной 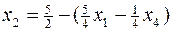 в целевую функцию. В результате получим:
в целевую функцию. В результате получим:
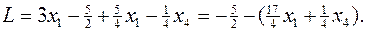
Тогда исходная задача будет иметь вид специальной формы задачи ЛП:
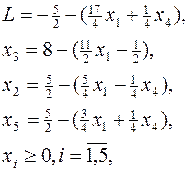
что и требовалось получить в результате решения вспомогательной задачи.
Двойственный симплекс-метод
Метод работает с теми же симплексными таблицами, что и прямой симплекс-метод для задачи на минимум. Сначала определяется переменная, подлежащая выводу из базиса, а затем переменная, вводимая в базис [1,3].
Вычислительная схема двойственного симплекс-метода
Шаг 0. Начинаем с симплексной таблицы, где 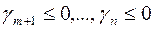 .
.
| B | 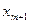 | … | 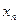 | |
| L | 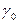 | 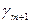 | … | 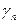 |
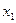 | 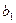 | 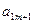 | … | 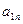 |
| … | … | ………….. | ||
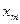 | 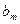 | 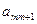 | … | 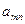 |
Шаг 1. Проверка на оптимальность. Если 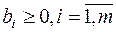 , то решение
, то решение 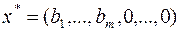 – оптимальное.
– оптимальное.
Шаг 2. Выбор ведущей строки. Выбираем среди номеров i, для которых 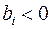 , номер k с максимальным по модулю значением
, номер k с максимальным по модулю значением
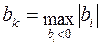 .
.
Строка k объявляется ведущей.
Шаг 3. Проверка на неразрешимость. Если в строке 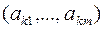 нет отрицательных элементов, то двойственная целевая функция неограниченная и, следовательно, прямая задача не имеет допустимых решений. Процесс решения завершается.
нет отрицательных элементов, то двойственная целевая функция неограниченная и, следовательно, прямая задача не имеет допустимых решений. Процесс решения завершается.
Шаг 4. Выбор ведущего столбца s. Выбираем среди отрицательных элементов строки 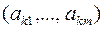 элемент с номером s, для которого выполняется равенство
элемент с номером s, для которого выполняется равенство
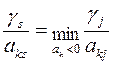 .
.
Столбец s объявляется ведущим, а элемент 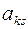 – ведущим элементом.
– ведущим элементом.
Шаг 5. Проводим стандартное преобразование симплексной таблицы (Шаг 6 из прямого симплекс-метода).
Пример решения задачи двойственным симплекс-методом
Решить задачу ЛП двойственным симплекс-методом:
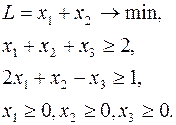
Приводим задачу к каноническому виду:
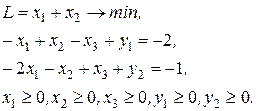
Знаки в ограничениях заменили противоположными для того, чтобы переменные 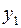 и
и 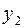 можно было взять в качестве базисных. Симплексная таблица имеет вид
можно было взять в качестве базисных. Симплексная таблица имеет вид
| b | 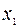 | 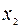 | 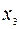 | |
| L | -1 | -1 | ||
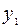 | -2 | -1 | -1 | |
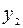 | -1 | -2 | -1 |
Таблица двойственно-допустимая, но не оптимальная. Выбираем ведущую строку – это строка переменной 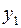 , ведущий столбец – это столбец переменной
, ведущий столбец – это столбец переменной 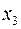 . После преобразования таблица принимает вид
. После преобразования таблица принимает вид
| b | 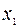 | 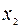 | 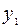 | |
| L | -1 | -1 | ||
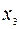 | -1 | -1 | ||
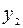 | -3 | -3 |
Так как в столбце b есть отрицательная переменная 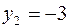 , то эту строку выбираем ведущей, а столбец переменной
, то эту строку выбираем ведущей, а столбец переменной 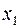 будет ведущим столбцом. После преобразования получаем таблицу:
будет ведущим столбцом. После преобразования получаем таблицу:
| b | 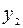 | 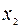 | 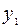 | |
| L | -1/3 | -1 | -1/3 | |
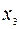 | 1/3 | -1 | -2/3 | |
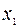 | -1/3 | -1/3 |
которая является оптимальной. Соответствующее оптимальное решение имеет вид 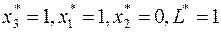 .
.
Двойственность в ЛП
Постановка задачи
Рассмотрим пару задач ЛП вида:
(I) (II)
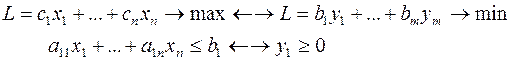
… …
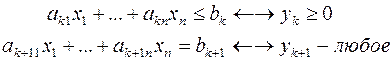
… …
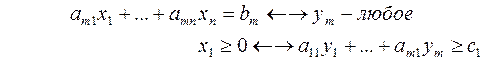
… …
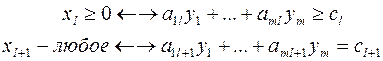
… …
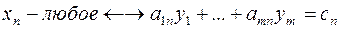 .
.
Задачу (I) называют прямой задачей ЛП, а (II) – двойственной. Неравенства задач (I) и (II), соответствующие друг другу (по стрелке), называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т. е. соотношение двойственности взаимное. Поэтому можно из такой пары задач любую считать прямой, а другую – двойственной.
Пример построения двойственной задачи
Построить двойственную задачу к следующей задаче ЛП:
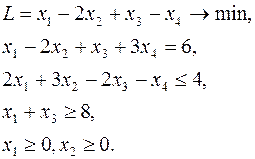
Прежде чем приступать к построению двойственной задачи, необходимо упорядочить запись исходной: согласовать знаки неравенств в ограничениях задачи с целевой функцией. Так как ЦФ минимизируется, то неравенства должны быть записаны с помощью знака « 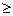 ». Для этого второе неравенство умножим на -1:
». Для этого второе неравенство умножим на -1:
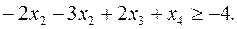
Теперь, вводя двойственные переменные 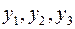 , запишем в соответствии с указанным правилом пару двойственных задач:
, запишем в соответствии с указанным правилом пару двойственных задач:
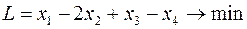 | 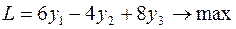 | |
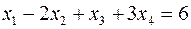 | 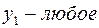 | |
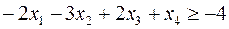 | 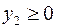 | |
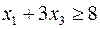 | 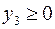 | |
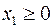 | 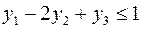 | |
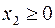 | 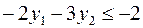 | |
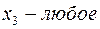 | 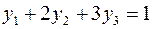 | |
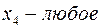 | 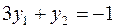 |
Задача слева – исходная прямая задача, задача справа – двойственная к исходной задаче.
Теоремы двойственности
Двойственность является одним из фундаментальных понятий в теории ЛП. Исключительно важную роль играют следующие утверждения, получившие названия теорем двойственности [1,3].
Первая теорема двойственности. Если одна из пары двойственных задач (I) и (II) разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают:
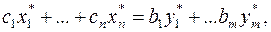
где 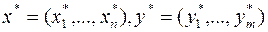 – оптимальные планы задач (I) и (II) соответственно.
– оптимальные планы задач (I) и (II) соответственно.
Говорят, что допустимые решения x, y удовлетворяют условиям дополняющей нежесткости (УДН), если при подстановке этих векторов в ограничения задач (I) и (II) хотя бы одно из любой пары сопряженных неравенств обращается в равенство.
Вторая теорема двойственности. 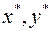 оптимальны в задачах (I) и (II) тогда и только тогда, когда они удовлетворяют УДН.
оптимальны в задачах (I) и (II) тогда и только тогда, когда они удовлетворяют УДН.
Пример решения пары двойственных задач
Используя теоремы двойственности, решить двойственную задачу, если известно решение прямой задачи:
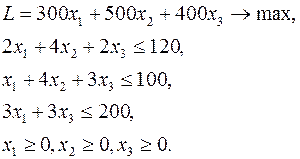 (20)
(20)
Пусть решение задачи найдено одним из стандартных методов: 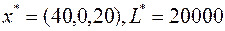 . Построим двойственную задачу:
. Построим двойственную задачу:
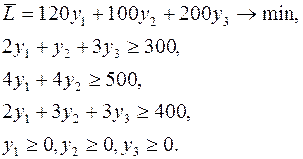 (21)
(21)
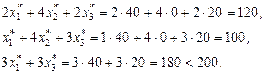 По первой теореме двойственности задача разрешима, причем
По первой теореме двойственности задача разрешима, причем 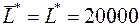 . Найдем оптимальный план
. Найдем оптимальный план 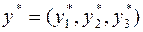 задачи (21), используя вторую теорему двойственности. Подставим координаты вектора
задачи (21), используя вторую теорему двойственности. Подставим координаты вектора 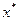 в ограничения задачи (20). Получим
в ограничения задачи (20). Получим
Следовательно, в силу УДН, неравенство 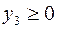 должно выполняться как равенство, т. е.
должно выполняться как равенство, т. е. 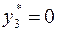 . Далее так как
. Далее так как 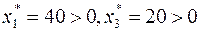 , то в силу УДН
, то в силу УДН
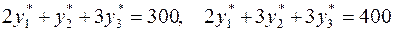 .
.
Получаем систему линейных уравнений и ре<
