Приведение произвольной пространственной системы сил к центру О

Дана пространственная система сил (рис. 7.5а). Приведем ее к центру О.

Силы необходимо параллельно перемещать, при этом образует­ся система пар сил. Момент каждой из этих пар равен произведению модуля силы на расстояние до центра приведения.

Тема 1.5. Пространственная система сил 53

В центре приведения возникает пучок сил, который может быть заменен суммарной силой (главный вектор) -F_гл (рис. 7.56).

Моменты пар сил можно сложить, получив суммарный момент системы М_гл (главный момент).

Таким образом, произвольная пространственная система сил приводится к главному вектору и главному моменту.

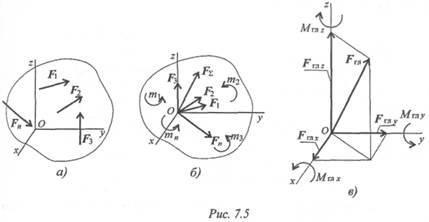
Главный вектор принято раскладывать на три составляющие, направленные вдоль осей координат (рис. 7.5в).

Обычно суммарный момент раскладывают на составляющие: три момента относительно осей координат.

Абсолютное значение главного вектора (рис. 7.56) равно

54 Лекция 7

Уравнения равновесия пространственной системы сил

При равновесии F_гл= 0; М_гл = 0. Получаем шесть уравнений равновесия:

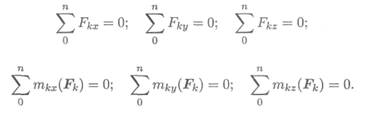
Шесть уравнений равновесия пространственной системы сил со­ответствуют шести независимым возможным перемещениям тела в пространстве: трем перемещениям вдоль координатных осей и трем вращениям вокруг этих осей.

Примеры решения задач

Пример 1.На тело в форме куба с ребром а — 10 см действуют три силы (рис. 7.6). Определить моменты сил относительно осей координат, совпадающих с ребрами куба.

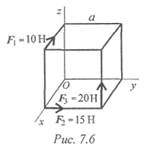
Решение

1. Моменты сил относительно оси Ох:

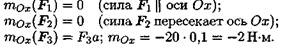
2. Моменты сил относительно оси Оу:

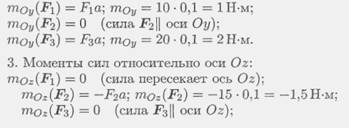
Тема 1.5. Пространственная система сил 55

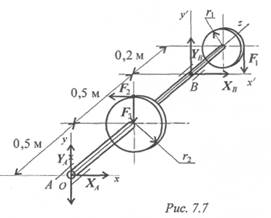
Пример 2.На горизонтальном валу закреплены два колеса, r1 = 0,4 м; гз = 0,8 м. Остальные размеры — на рис. 7.7. К коле­су 1 приложена сила F1, к колесу 2 — силы F₂ = 12 кН, F3= 4кН.

Определить силу F1и реакции в шарнирах А и В в состоянии равновесия.

Напомним:

1. При равновесии вы­полняются шесть рав­нений равновесия.

Уравнения моментов следует составлять от­носительно опор А и В.

2. Силы F₂\\Ox; F1\\Oy; F3\\Оу.

Моменты этих сил относительно соответ­ствующих осей равны нулю.

3. Расчет следует завершить проверкой, ис­пользовав дополнительные уравнения равновесия.

Решение

1. Определяем силу F1, составив уравнение моментов сил отно­сительно оси Oz:

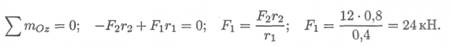
2. Определяем реакции в опоре А. На опоре действуют две со­ставляющие реакции (Yа;ХA).

Составляем уравнение моментов сил относительно оси Ох' (в опоре B).

Поворот вокруг оси Ох' не происходит:

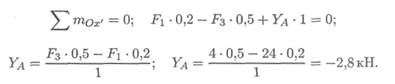
56 Лекция 7

Знак «минус» означает, что реакция направлена в противоположную сторону.

Поворот вокруг оси Оу' не происходит, составляем уравнение моментов сил относительно оси Оу' (в опоре В):

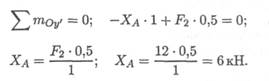
3. Определяем реакции в опоре В. На опоре действуют две составляющие реакции (ХВ; Yb). Составляем уравнение моментов сил
относительно оси Ох (опора А):

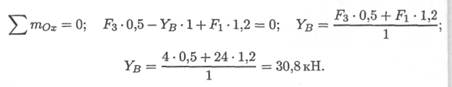
Составляем уравнение моментов относительно оси Оу (опора А):

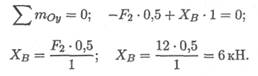
4. Проверка. Используем уравнения проекций:

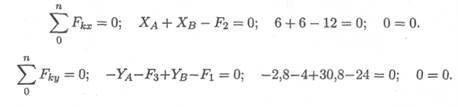
Расчет выполнен верно.

Контрольные вопросы и задания

1. Запишите формулы для расчета главного вектора простран­ственной системы сходящихся сил.

Тема 1.5. Пространственная система сил 57

2. Запишите формулу для расчета главного вектора простран­ственной системы произвольно расположенных сил.

3. Запишите формулу для расчета главного момента простран­ственной системы сил.

4. Запишите систему уравнений равновесия пространственной системы сил.

5. Какое из уравнений равновесия нужно использовать для опре­деления реакции стержня R1 (рис. 7.8)?

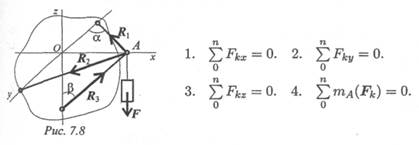
6. Определите главный момент системы сил (рис. 7.9). Точка
приведения — начало координат. Координатные оси совпадают с
ребрами куба, ребро куба равно 20 см; F1 = 20 кН; F2 = 30 кН.

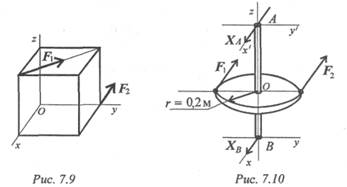
7. Определите реакцию ХВ (рис. 7.10). Вертикальная ось со
шкивом нагружена двумя горизонтальными силами. Силы F1 и F2 параллельны оси Ох. АО = 0,3 м; ОB = 0,5 м; F1 = 2 кН; F2 = 3,5 кН.

Рекомендация. Составить уравнение моментов относительно оси Оу' в точке А.

58 Лекция 7

8. Ответьте на вопросы тестового задания.

Тема 1.5. Статика.