Приведение системы сил к данному центру

Решим теперь задачу о приведении произвольней системы сил к данному центру, т. е. о замене данной системы сил другой, ей эквивалентной, но значительно более простой, а именно состоящей, как мы увидим, только из одной силы и пары.

Пусть на твердое тело действует произвольная система сил (рис. 40, а).

Выберем какую-нибудь точку О за центр приведения и, пользуясь теоремой, доказанной в § 11, перенесем все силы в центр О, присоединяя при этом соответствующие пары (см. рис. 37, б). Тогда на тело будет действовать система сил

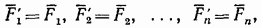
приложенных в центре О, и система пар, моменты которых согласно формуле (18) равны:

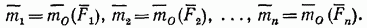
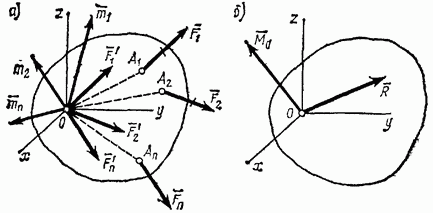
Рис. 40

Сходящиеся силы, приложенные в точке О, заменяются одной силой R, приложенной в точке О. При этом или, согласно равенствам (19),

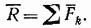
Чтобы сложить все полученные пары, надо сложить векторы моментов этих пар. В результате система пар заменится одной парой, момент которой или, согласно равенствам (20),

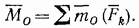
Как известно, величина R, равная геометрической сумме всех сил, называется главным вектором системы величина равная геометрической сумме моментов всех сил относительно центра О, называется главным моментом системы сил относительно этого центра.

Таким образом, мы доказали следующую теорему о приведении системы сил: любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой R, равной главному вектору системы сил и приложенной в центре приведения О, и одной парой с моментом 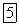равным главному моменту системы сил относительно центра О (рис. 40, б).

Заметим, что сила R не является здесь равнодействующей данной системы сил, так как заменяет систему сил не одна, а вместе с парой.

Из доказанной теоремы следует, что две системы сил, имеющие одинаковые главные векторы и главные моменты относительно одного и того же центра, эквивалентны (условия эквивалентности систем сил).

Отметим еще, что значение R от выбора центра О, очевидно, не зависит. Значение же при изменении положения центра О может в общем случае изменяться вследствие изменения значений моментов отдельных сил. Поэтому всегда необходимо указывать, относительно какого центра определяется главный момент.

Рассмотрим в заключение два частных случая: 1) если для данной системы сил то она приводится к одной паре сил с моментом . В этом случае значение не зависит от выбора центра О, так как иначе получилось бы, что одна и та же система сил заменяется разными, не эквивалентными друг другу парами, что невозможно; 2) если для данной системы сил приводится к одной силе, т. е. к равнодействующей, равной R и приложенной в центре О.

Теорема Вариньона

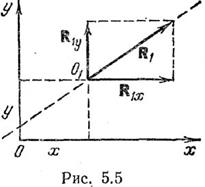
Теорема Вариньона. Если рассматриваемая плоская система сил приводится к равнодействующей, то момент этой равнодействующей относительно какой-либо точки равен алгебраической сумме моментов всех сил данной системы относительно той оке самой точки. Предположим, что система сил приводится к равнодействующей R, проходящей через точку О. Возьмем теперь в качестве центра при­ведения другую точку O₁. Главный момент (5.5) относительно этой точки равен сумме моментов всех сил: M_O1Z=åM_o1z(F_k) (5.11). С другой стороны, имеем M_O1Z=M_Olz(R), (5.12) так как главный момент для центра приведения О равен нулю (M_Oz=0). Сравнивая соотношения (5.11) и (5.12), получаем M_O1z(R)=åM_OlZ(F_k); (5.13) ч.т.д. При помощи теоремы Вариньона можно найти уравнение линии действия равнодействующей. Пусть равнодействующая R₁ приложена в какой-либо точке О₁ с координатами х и у (рис. 5.5) и известны главный вектор F_o и главный момент М_Оя при центре приведения в начале координат. Так как R₁=F_o, то составляющие равнодей­ствующей по осям х и у равны R_lx=F_Ox=F_Oxi и R_ly=F_Oy=F_oyj. Согласно теореме Вариньона мо­мент равнодействующей относительно на­чала координат равен главному моменту при центре приведения в начале коорди­нат, т. е. М_оz=M_Oz(R₁)=xF_Oy–yF_Ox. (5.14). Величины M_Oz, F_Ox и F_oy при переносе точки приложения равнодействующей вдоль ее линии действия не изменяются, следовательно, на координаты х и у в уравнении (5.14) можно смотреть как на текущие координаты ли­нии действия равнодействующей. Таким образом, уравнение (5.14) есть уравнение линии действия равнодействующей. При F_ox≠0 его можно переписать в виде y=(F_oy/F_ox)x–(M_oz/F_ox).

Экзаменационный билет № 21

1. Сложное движение. Теорема о сложении скоростей.

2. Равновесие плоской системы сил. Формы равновесия.

3. Задача.

1Теоре́ма о сложе́нии скоросте́й — одна из теорем кинематики, связывает между собой скорости материальной точки в различных системах отсчёта. Утверждает, что при сложном движенииматериальной точки её абсолютная скорость равна сумме относительной и переносной скоростей^[1][2].

Сложное движение.

Движение в механике всегда рассматривается по отношению к какой-либо системе отсчёта. Однако в некоторых случаях бывает целесообразно или даже необходимо изучать движение материальной точки (МТ) относительно двух различных систем отсчёта одновременно. Одну из этих систем отсчёта условно считают неподвижной, базовой, а другую полагают движущейся относительно первой. Тогда движение точки можно рассматривать, как состоящее из двух движений: первое — движение относительно движущейся системы отсчёта, второе — движение вместе с движущейся системой относительно неподвижной. Такое движение точки называют сложным или составным.

Определения[править | править вики-текст]

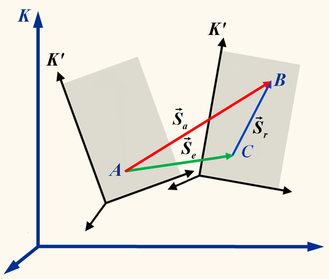
Условно неподвижную систему отсчёта принято называть абсолютной. Соответственно, абсолютными называют движение, перемещение, скорость и ускорение точки относительно этой СО. На рисунке система отсчёта K выбрана в качестве абсолютной.

Условно подвижную систему отсчёта принято называть относительной. Движение, перемещение, скорость и ускорение точки относительно этой системы также именуют относительными. Система K' на рисунке является относительной.

Движение, совершаемое подвижной системой K' и всеми жёстко связанными с нею точками пространства^[3] относительно системы К, называютперено́сным. Если некоторая МТ движется относительно подвижной системы K', то в общем случае та точка системы K', в которой в данный момент находится МТ, также движется относительно неподвижной системы К. Мгновенную скорость этой точки системы K' называют переносной скоростьюМТ.

Доказательство[править | править вики-текст]

Пусть МТ в некоторый момент времени находилась в точке А, а через промежуток времени 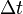оказалась в точке В (см. рис.). Тогда её перемещение относительно системы К (абсолютное перемещение) будет равно 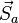. Точка А подвижной системы K' за время переместилась вместе с K' и оказалась в точке С, совершив перемещение относительно системы К (переносное перемещение), изображённое на рисунке вектором 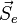. С точки зрения наблюдателя, связанного с системой K', точка С является той точкой, в которой МТ находилась первоначально, поэтому вектор 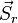представляет собой перемещение МТ относительно подвижной системы K', то есть относительное перемещение. Из сказанного и векторной диаграммы на рисунке следует

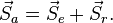
Деля данное равенство на промежуток времени 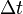, а затем устремляя его к нулю, в пределе получаем

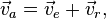
где 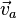— абсолютная, 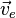— переносная, а 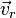— относительная скорость движения МТ.

Полученное равенство является математическим выражением теоремы о сложении скоростей, которая формулируется так:

Теорему о сложении скоростей называют также правилом параллелограмма скоростей^[4].

22.2 Равновесие произвольной плоской системы сил

При равновесии произвольной плоской системы сил уравнения равновесия могут быть записаны в виде

∑x_i=0;

∑y_i=0;

∑M_o=0,

причем оси и точка O , относительно которой пишется уравнение моментов, выбираются произвольно.

Уравнения равновесия также могут быть записаны иначе:

∑x_i =0;

∑M_A=0;

∑M_B=0.

Здесь ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B .

∑M_A=0;

∑M_B=0;

∑M_C=0.

В задачах такого типа число неизвестных плоской системы сил не должно превышать трех, иначе система станет статически неопределимой.