Порядок построения вариационных рядов

Выборочная статистическая совокупность, полученная в процессе учета наблюдений, как правило, записывается в произвольной последовательности. Обработка таких данных начинается с их систематизации, т.е. объединения в относительно однородные группы по некоторому признаку. В случае числового непрерывного признака группировка выполняется в описанной ниже последовательности. Проиллюстрируем это на примере выборочной совокупности, представляющей собой измерения высот и диаметров у 200 деревьев.

1. В исходной совокупности данных находим минимальное и максимальное значения признака. Для диаметров D_min = 15,6; D_max= 51,0. Для высот H_min = 17,7; H_max = 29.

2. С учетом объема выборки n=200 принимаем количество интервалов k=8 в будущих статистических рядах, согласно рекомендаций, приведенных в методическом указании.

3. Определяем величины интервалов будущих вариационных рядов следующим образом:

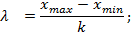
где λ – величина интервала.

Полученную величину следует округлить таким образом, чтобы точность представления исходных данных и величины интервала была одинаковой, а последняя цифра – нечетной.

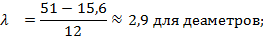
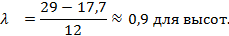
4. Определяем границы первого интервала вариационного ряда таким образом, чтобы минимальное значение в выборке попало в его середину:

;

;

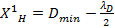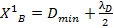где x¹_н – нижняя граница первого интервала, x¹_в – верхняя граница первого интервала.

для диаметров

;

;

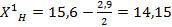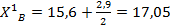для высот

;

;

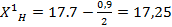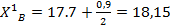5. Вычисляем границы остальных интервалов, пользуясь формулами:

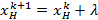
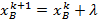
где x_н^k – нижняя граница k-го интервала; x_в^k – верхняя граница k-го интервала.

6. Определим количество наблюдений, попавшее в интервалы вариационного ряда, регистрируя наблюдения методом конверта (Таблица 1). Разноску частот удобно выполнять, пользуясь вспомогательной таблицей.

Таблица 1 ─ Шифры частот, используемые при регистрации наблюдений

Число наблюдений
Шифр частот

7. В качестве значений для сформированных классовых интервалов в дальнейших расчетах будем использовать середины классовых интервалов, которые вычислим по следующей формуле:

,

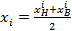где x_i – значения классовых интервалов.

8. При анализе массовых данных наряду с частотами вариационных рядов часто используют накопленные частоты, которые вычисляют как сумму частот текущего и всех предшествующих интервалов.

Результаты группировки деревьев по диаметрам и высотам для рассматриваемого примера приведены в таблицах 2 и 3.

Таблица 2 ─ Распределение наблюдений по интервалам (диаметры)

Границы интервалов	Шифр частот	Частоты	Накопленные частоты	Среднее значения интервалов
14,15	17,05				15,6
17,05	19,95				18,5
19,95	22,85				21,4
22,85	25,75				24,3
25,75	28,65				27,2
28,65	31,55				30,1
31,55	34,45
34,45	37,35				35,9
37,35	40,25				38,8
40,25	43,15				41,7
43,15	46,05				44,6
46,05	48,95				47,5
48,95	51,85				50,4
Итого

Таблица 3 ─ Распределение наблюдений по интервалам (высоты)

Границы интервалов	Шифр частот	Частоты	Накопленные частоты	Среднее значения интервалов
17,25	18,15				17,7
18,15	19,05				18,6
19,05	19,95				19,5
19,95	20,85				20,4
20,85	21,75				21,3
21,75	22,65				22,2
22,65	23,55				23,1
23,55	24,45
24,45	25,35				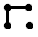24,9
25,35	26,25				25,8
26,25	27,15				26,7
27,15	28,05				27,6
28,05	28,95				28,5
28,95	29,85				29,4
Итого

В дальнейших расчетах будем использовать не сами диаметры и высоты деревьев, полученные в результате измерений, а середины интервалов и частоты составленных нами вариационных рядов