Процесса посредством больших выборок

Статистический анализ точности технологического процесса производится после того, как станок проработал некоторое время, необходимое для стабилизации температуры технологической системы. Это время колеблется в пределах 1-2 часов. В результате погрешности обработки, вызываемые температурными деформациями элементов системы, превратятся из функциональных в постоянные.

Статистический анализ посредством больших выборок заключается в следующем. Со станка берется текущая выборка, состоящая из деталей, изготовленных подряд одна за другой при неизменной настройке и других неизменных условиях. Объем выборки устанавливается в зависимости от желаемой точности и надежности меры рассеяния 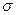(СКО) суммарной погрешности обработки. Для практического использования можно принять точность оценки 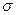по выборочному S (дисперсия), равную:

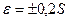
с вероятностью 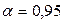. Тогда объем выборки достаточно сделать равным n=50.

Все детали должны быть измерены шкальным измерительным инструментом с ценой деления измерительной шкалы, равной

,

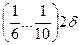где 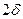- допуск на измеряемый размер.

На основании результатов измерения деталей выборки составляется таблица распределения размеров выборки.

Ниже приведена таблица 1 результатов измерения колебания длины общей нормали 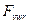зубчатого колеса 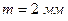, числом зубьев 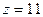, обработанных шевером прикатником с параметрами , , .

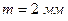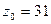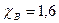Таблица 1 - Колебание длины общей нормали 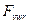, мкм

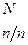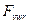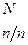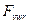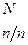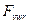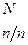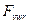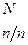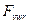Далее производим группировку исходных данных. С этой целью определяем размах варьирования размеров:

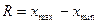
где 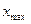- максимальное значение ,

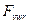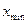- минимальное значение ,

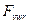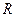- размах значений .

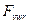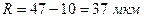
Размах разбивается на n интервалов группировки. Для партии из N=50…100 объектов исследования число интервалов принимается равным от 6 до 9. Принимаем n=7.

Ширина интервалов принимается одинаковой, равной:

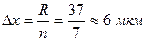
Тогда границы интервалов могут быть записаны:

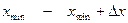
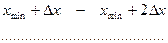
Для компенсации погрешности измерения необходимо, чтобы величина 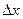была больше цены деления шкалы средства измерения, которым проводились измерения объектов.

Для облегчения вычислений частот и частностей значений случайной величины в интервале построим вспомогательную таблицу:

Таблица 2 – Вычисление частот и частностей

№ интервала	Интервал	Середина интервала	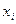Частота	Частность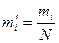
свыше	до (включит.)	Условное обозначение	Цифровое значение
						0,08
						0,32
						0,30
						0,18
						0,10
					-	-
						0,02

По данным таблицы 2 построим гистограмму распределения случайной величины, отражающей дифференциальный закон распределения случайной величины. Масштаб гистограммы выбирают так, чтобы ее высота относилась к основанию как 5:8.

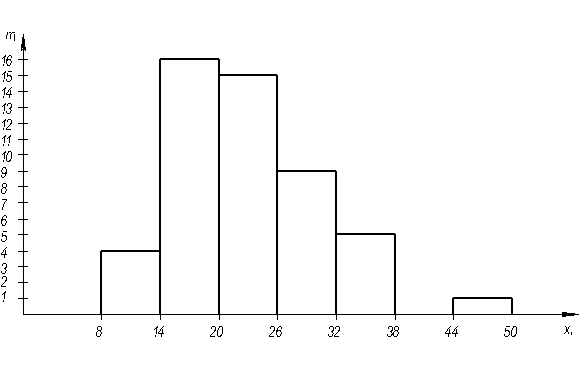
Рисунок 1 – Гистограмма

Строим полигон распределения случайной величины.

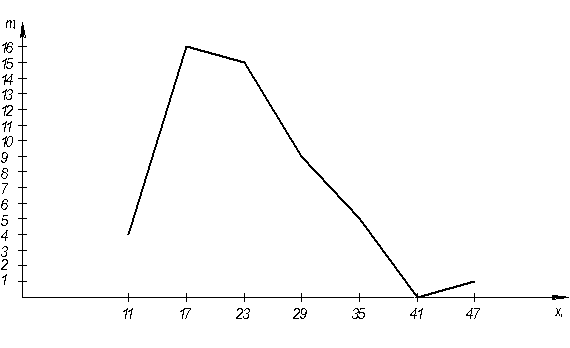
Рисунок 2 – Полигон

Полигон распределения называют эмпирическим распределением случайной величины.

Для вычисления параметров эмпирического распределения строим вспомогательную таблицу 3.

Обозначим через 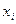середины интервалов. Примем 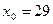. Тогда .

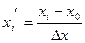Таблица 3 – Вычисление параметров эмпирического распределения

№ интервала	Середина интервала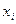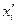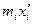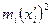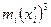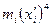
			-3	-12		-108
			-2	-32		-128
			-1	-15		-15
		-
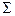				-51		-219

Вычисляем начальные моменты:

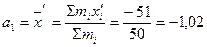
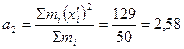
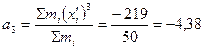
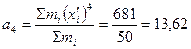
Вычисляем центральные моменты:

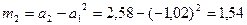
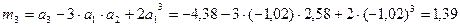
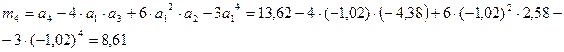
Вычисляем среднее значение и СКО:

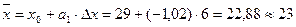
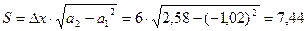
Вычисляем показатель асимметрии кривой распределения:

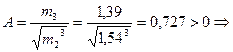
эмпирическая кривая сдвинута влево относительно кривой нормального распределения.

Вычисляем показатель крутизны (эксцесса):

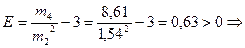
эмпирическая кривая выше кривой нормального распределения.

Построим графики эмпирической и выровненной кривой распределения. Вычисления произведем с помощью вспомогательной таблицы по нормальному закону распределения случайной величины.

Таблица 4 – Вычисление параметров выровненной кривой распределения

№ интервала	Середина интервала	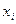			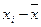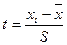Ф(t)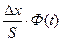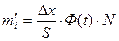
			-12	-1,61	0,1092	0,0881	4,405
			-6	-0,81	0,2874	0,2318	11,59
					0,3989	0,3217	16,085
				0,81	0,2874	0,2318	11,59
				1,61	0,1092	0,0881	4,405
		-		2,42	0,0213	0,0172	0,86
				3,23	0,0022	0,0018	0,09
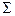		49,025

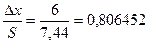
По данным таблицы 4 строим выровненную и эмпирическую кривые распределения:

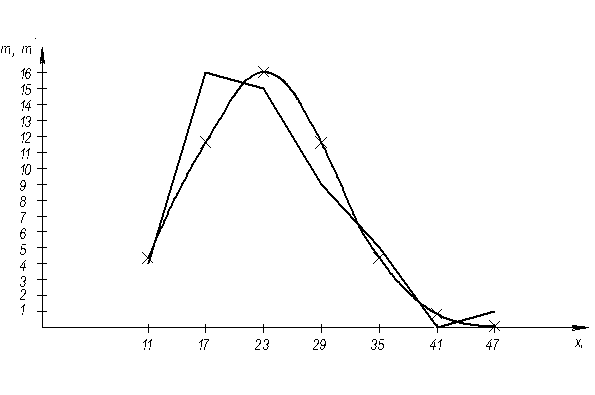
Рисунок 3 – Эмпирическая и выровненная кривые распределения

Проверим правильность выдвинутой гипотезы о виде закона распределения случайной величины с помощью критерия согласия Пирсона 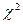. При использовании этого критерия за меру расхождения экспериментальных данных с теоретическим законом (нормальным законом распределения в данном случае) принимается сумма квадратов отклонений частностей 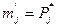от теоретической вероятности 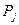попадания отдельного результата измерений в j-тый интервал. Причем каждое слагаемое принимается с весовым коэффициентом

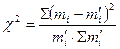
Выполним вычисления с помощью специальной таблицы. Если в некоторые интервалы попадает менее 5 значений, то они объединяются с соседними.

Таблица 5 – Вычисление коэффициента согласия Пирсона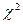

№
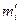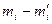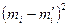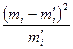			4,405 11,59	15,995	4,005	16,0400	1,0028
		16,085	-1,085	1,1772	0,0732
		11,59	-2,59	6,7081	0,5788
	-		4,405 0,86 0,09	5,355	0,645	0,4160	0,0777
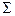		1,7325

Определяем :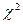

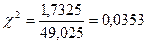
После нахождения величины 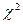следует определить число степеней свободы ,

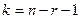где n – число сравниваемых частот (объединенные частоты на концах принимаются за одну частоту);

r – число параметров теоретической функции распределения (нормальный закон распределения двухпараметрический).

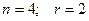
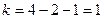
По таблице определяем:

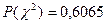
Так как 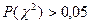, то кривые согласуются и принятый закон соответствует нормальному.

Зная параметры нормального распределения, можно дать оценку точности обработки на рассматриваемой технологической операции, т.е. сделать вывод о степени соответствия точности операции требованиям технологического процесса и о правильности настройки станка (если рассеяние будет соответствовать допуску, а математическое ожидание середине поля допуска).

Технологическая операция по точности соответствует требованиям технологического процесса, если соблюдается услови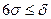е , где 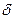- допуск на размер.

При несоблюдении указанного условия появляется брак, процент которого для закона нормального распределения может быть определен на основе функции Лапласа. В частности, для наружного диаметра вала имеем следующий процент неисправимого брака:

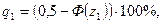
где

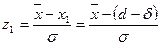
Процент исправимого брака:

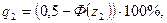
где

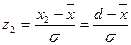
Значение функции Лапласа принимается согласно Приложению.

Настройка станка не влияет на величину 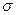, изменяет значение 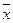и, следовательно, не изменяя формы кривой распределения, смещает ее вдоль оси абсцисс.

Для уменьшения поля рассеяния размеров необходимо выполнить комплекс технологических мероприятий (повысить жесткость технологической системы, уменьшить колебания припуска и твердости заготовки, снизить погрешность установки заготовки на станке и т.п.). Исправить ошибки в настройке станка можно введением дополнительной поднастройки.

Рассмотрим наш пример.

Для выровненной кривой

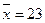, S=7,4.

Число степеней свободы:

k=N-1=50-1=49

Задаемся надежностью определения допуска Р=0,9. Задаемся вероятностью 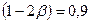, т.е. задаемся площадью кривой распределения, которая входит в определяемый нами допуск. Из таблиц значений l для Р=0,9, 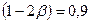и N=49 находим l=1,91. Тогда границы поля допуска:

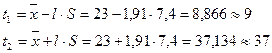
Находим координату середины поля допуска и половину поля допуска:

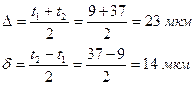
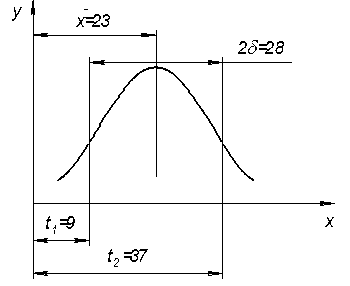
Таким образом, если за поле допуска брать величину 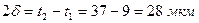, то с вероятностью Р=0,9 из всех будущих наблюдений 90% будут лежать в этом интервале.

ЗАДАНИЕ 3