Непрерывные случайные величины. плотность распределения вероятностей случайной величины
С помощью рассмотренных дискретных случайных величин невозможно описать реальные случайные эксперименты. Действительно, таким величинам, как размеры любых физических объектов, температура, давление, длительность тех ли иных физических процессов, нельзя приписать дискретное множество возможных значений. Естественно считать, что это множество заполняет какой-то числовой промежуток. Поэтому вводится понятие непрерывной случайной величины.
Непрерывной случайной величиной называют такую случайную величину Х, множество значений которой 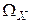 – некоторый числовой интервал.
– некоторый числовой интервал.
Рассмотрим примеры непрерывных случайных величин.
1. Х – промежуток времени между двумя отказами (сбоями) вычислительной машины. Тогда 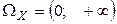 .
.
2. Х – высота подъема воды в половодье. В этом случае 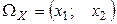 .
.
Ясно, что для непрерывной случайной величины, значения которой сплошь заполняют некоторый интервал оси абсцисс, ряд распределения построить невозможно. Во-первых, нельзя перечислить одно за другим возможные значения и, во-вторых, как мы покажем далее, вероятность отдельного значения непрерывной случайной величины равна нулю.
В противном случае, т.е. если бы каждому отдельному значению непрерывной случайной величины соотнести ненулевую вероятность, то при суммировании всех вероятностей можно получить число, отличное от единицы, так как множество значений 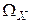 непрерывной случайной величины несчетно (значения заполняют сплошь некоторый интервал).
непрерывной случайной величины несчетно (значения заполняют сплошь некоторый интервал).
Пусть множество 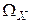 содержит несчетное множество значений непрерывной случайной величины Х. Систему подмножеств
содержит несчетное множество значений непрерывной случайной величины Х. Систему подмножеств 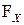 образуют любые подмножества, которые могут быть полученыиз множества
образуют любые подмножества, которые могут быть полученыиз множества 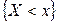 ,
, 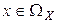 , путем применения счетного числа раз операций объединения, пересечения, дополнения. Система
, путем применения счетного числа раз операций объединения, пересечения, дополнения. Система 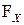 , следовательно, будет содержать множества вида {х1<Х<х2},
, следовательно, будет содержать множества вида {х1<Х<х2},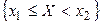 ,
, 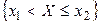 ,
, 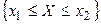 ,
, 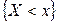 ,
, 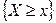 ,
, 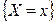 .
.
Для определения на этих множествах вероятностноймеры введем понятие плотности распределения вероятностей.
Определение 2.5. Плотностью распределения вероятностей р(х) непрерывной случайной величины Х называется предел, если он существует, отношения вероятности попадания случайной величины Х на интервал 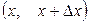 , примыкающей к точке х, к длине этого интервала, когда последняя стремится к нулю т. е.
, примыкающей к точке х, к длине этого интервала, когда последняя стремится к нулю т. е.
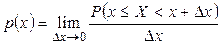 (2.4)
(2.4)
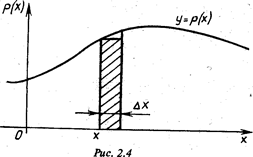
Кривая, изображающая плотность распределения вероятностей (плотность вероятности) непрерывной случайной величины, называется кривой распределения. Например, кривая распределения может иметь вид, как на рис. 2.4.
Следует отметить, что если р (х) умножить на 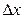 , то величина р(х)
, то величина р(х) 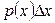 , называемая элементом вероятности, характеризует вероятность того, что Х принимает значения из интервала длиной
, называемая элементом вероятности, характеризует вероятность того, что Х принимает значения из интервала длиной 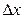 , примыкающего к точке х. Геометрически – это площадь прямоугольника со сторонами
, примыкающего к точке х. Геометрически – это площадь прямоугольника со сторонами 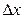 и р(х) (см. рис. 2.4).
и р(х) (см. рис. 2.4).
Тогда вероятность попадания непрерывной случайной величины Х на отрезок 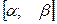 будет равна сумме элементов вероятности на всем этом отрезке
будет равна сумме элементов вероятности на всем этом отрезке 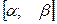 , т.е. площади криволинейной трапеции, ограниченной кривой у = р (х), осью Ох и прямыми х = а, х = β:
, т.е. площади криволинейной трапеции, ограниченной кривой у = р (х), осью Ох и прямыми х = а, х = β:
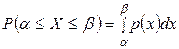 , (2.5)
, (2.5)
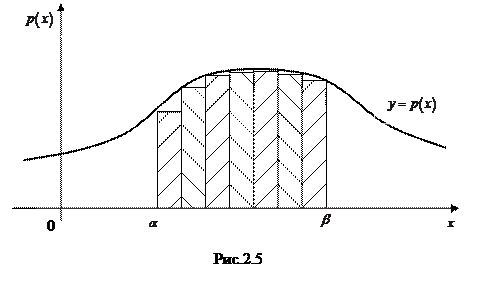
так как площадь заштрихованной фигуры будет стремиться к площади криволинейной трапеции при 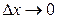 (рис. 2.5).
(рис. 2.5).
Плотность вероятности обладает следующими свойствами.
1°. р(х) 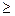 0
0 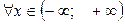 , так как предел неотрицательных величин – величина неотрицательная.
, так как предел неотрицательных величин – величина неотрицательная.
2°. 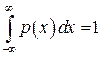 , так как вероятность того, что непрерывная случайная величина принимает значения из интервала
, так как вероятность того, что непрерывная случайная величина принимает значения из интервала 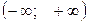 , т.е. вероятность достоверного события равна единице.
, т.е. вероятность достоверного события равна единице.
3°. р(х) — непрерывна или кусочно непрерывна.
Таким образом, с помощью формулы (2.5) вводится нормированная вероятностная мера на любых подмножествах 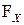 множества
множества 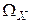 .
.
Функция распределения случайной величины Х – это функция F(х) действительной переменной х, определяющая вероятность того, что случайная величина принимает значения, меньшие некоторого фиксированного числа х, т.е. 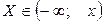 :
: 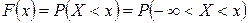 .
.
Тогда из формулы (2.5) следует, что для любых 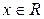
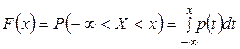 . (2.6)
. (2.6)
Геометрически функция распределения есть площадь фигуры, лежащей левее точки х, ограниченной кривой распределения у = р(х) и осью абсцисс. Из формулы (2.6) и теоремы Барроу для случая, когда р (х) непрерывна, следует, что
р(х) = 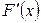 (2.7)
(2.7)
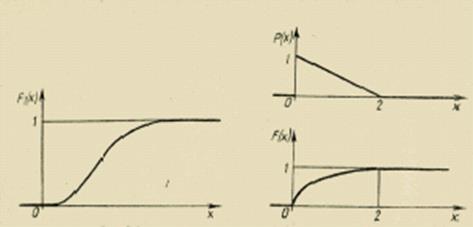
Рис.2.6 Рис.2.7
Это равенство нарушается в точках разрыва плотности вероятностей. График F(х) непрерывной случайной величины Хможет иметь вид кривой, приведенной на рис. 2.6.
Дадим строгое определенне непрерывной случайной величины.
Определение 2.6. Случайная величина Х называегся непрерывной, если существует неотрицательная функция р(х), что для любых 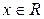 выполняется равенство (2.6).
выполняется равенство (2.6).
Функция распределения F(х), удовлетворяющая равенству (2.6), называется абсолютно непрерывной.
Итак, функция распределения непрерывной случайной величины задает абсолютно непрерывное распределение случайной величины.
Для непрерывной случайной величины Х справедлива следующая теорема.
Теорема 2.4. Вероятнсть отдельного значения непрерывной случайной величины Х равна нулю:
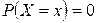 .
.
Доказательство. По теореме 2.3 вероятность отдельного значения равна:
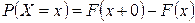 .
.
Так как для непрерывной случайной величины 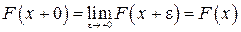 , то
, то 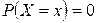 .
. 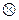
Из доказанной теоремы следует справедливость равенств:
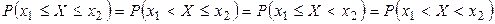 .
.
Действительно, 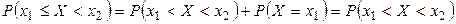 , так как
, так как 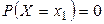 и т.д.
и т.д.
Таким образом, для вычисления вероятностей произвольных событий 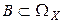 , где
, где 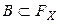 надо задать на множестве значений
надо задать на множестве значений 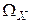 непрерывной случайной величины либо функцию распределения F(х), либо плотность распределения вероятностей р(х).
непрерывной случайной величины либо функцию распределения F(х), либо плотность распределения вероятностей р(х).
Пример 2.4. Случайная величина Х имеет плотность распределения вероятностей
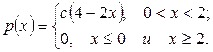
Найти параметр с и функцию распределения F(х). Построитьграфики функций р(х) и F(х).
Решение. Для нахождения параметра с, воспользуемся свойством 2○ плотности распределения вероятностей: 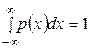 . Подставив значение плотности, получим
. Подставив значение плотности, получим 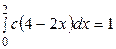 . Вычислив интеграл
. Вычислив интеграл 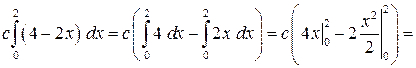
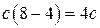 , найдем значение с из равенства:
, найдем значение с из равенства: 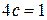 ,
, 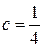 .
.
Плотность распределения вероятностей примет вид
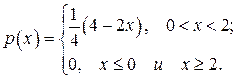
Поскольку плотность задана при помощи трех формул, то вычисление функции распределения зависит от расположения 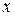 на числовой оси. Если:
на числовой оси. Если:
1) 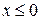 , то воспользовавшись формулой (2.6), получим
, то воспользовавшись формулой (2.6), получим
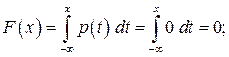
2) 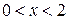 , то
, то 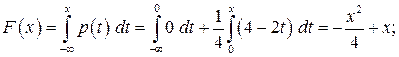
3) 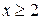 , то
, то
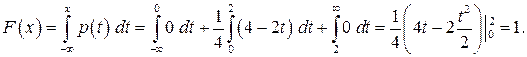
Функция распределения будет иметь вид:
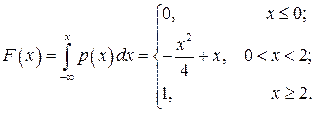
На рис. 2.7 приведены графики плотности распределения вероятностей р(х) и функции распределення F(х).
Ответ:параметр 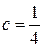 ; функция распределения
; функция распределения 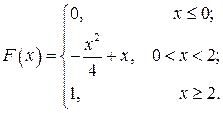
Пример 2.5. Случайная величина Х задана функцией распределения

Найти плотность распределения вероятностей р(х) н вычислить вероятность того, что случайная величина примет значение из интервала (0; 2).
Решение. Так как в точках непрерывности функции распределения 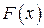 плотность распределения вероятностей равна производной
плотность распределения вероятностей равна производной 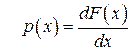 , то
, то
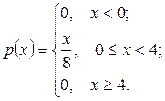
Вероятность того, что случайная величина примет значение из интервала (0; 2) вычислим по формуле (2.5): 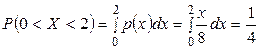 , так как если
, так как если 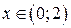 , то
, то 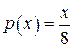 .
.
Эту вероятность можно вычислить также и с помощью функции распределения:
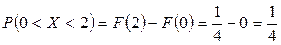 .
.
Ответ:вероятность того, что случайная величина примет значение из интервала (0; 2), равна 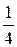 .
.
Часто для решения практических задач достаточно знать числовые характеристики случайных величин, например, среднее значение, вокруг которого происходит случайный разброс; степень этого разброса и ряд других признаков. В следующем параграфе мы и определим эти числовые характеристики.
Вопросы для самопроверки
1.Чем отличаются дискретные случайные величины от непрерывных случайных величин?
2.Почему для непрерывных случайных величин невозможно построить ряд распределения?
3.Что характеризует элемент вероятности 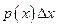 ?
?
4.Как вычислить вероятность попадания непрерывной случайной величины на промежуток?
5.Как вычислить функцию распределения 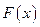 непрерывной случайной величины
непрерывной случайной величины 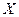 ?
?
6.Почему плотность распределения 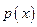 непрерывной случайной величины
непрерывной случайной величины 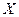 является неотрицательной функцией?
является неотрицательной функцией?
7.Чему равна вероятность отдельного значения 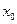 непрерывной случайной величины
непрерывной случайной величины 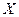 ?
?
