Тема: Исследование сходимости знакочередующихся рядов. Исследование числовых рядов на абсолютную и условную сходимость
Цель: Формирование навыков исследования сходимости знакочередующихся рядов; исследования числовых рядов на абсолютную и условную сходимость
Время выполнения: 2 часа
Требования к выполнению практической работы:
1.Ответить на теоретические вопросы.
2.Оформить задания в тетради для практических работ.
Теоретический материал
Числовой ряд
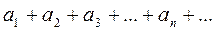 (23.1)
(23.1)
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа.
Числовой ряд (23.1) называется знакочередующимся, если любые два стоящие рядом члена имеют противоположные знаки. Этот ряд является частным случаем знакопеременного ряда.
Признак сходимости Лейбница для знакочередующихся рядов. Если члены знакочередующегося ряда (23.1) монотонно убывают по абсолютной величине и общий член 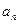 стремиться к нулю при
стремиться к нулю при 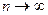 , то ряд (23.1) сходится.
, то ряд (23.1) сходится.
Этот признак служит достаточным признаком сходимости знакочередующихся рядов.
Знакопеременный ряд (23.1) называется абсолютно сходящимся, если сходится ряд
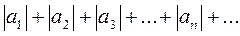 , (23.2)
, (23.2)
составленный из абсолютных величин его членов, то есть всякий абсолютно сходящийся ряд является сходящимся.
Если знакопеременный ряд (23.1) сходится, а составленный из абсолютных величин его членов ряд (23.2) расходится, то данный ряд (23.1) называется условно (неабсолютно) сходящимся. Заметим, что из расходимость ряда (23.2) в общем случае не следует расходимость ряда (23.1).
Для установления абсолютной сходимости знакопеременного (и знакочередующегося) ряда используются те же признаки, что и для сходимости ряда с положительными членами.
Для решения вопроса об абсолютной или условной сходимости знакочередующегося ряда необходимо рассмотреть ряд, составленный из абсолютных величин членов знакочередующегося ряда.
Если при исследовании этого ряда с помощью одного из признаков сходимости (признака Даламбера, признака сравнения рядов) ряд окажется сходящимся, то данный знакочередующийся ряд сходится абсолютно; если же ряд окажется расходящимся, то знакочередующийся ряд сходится условно.
Примеры
Исследовать на сходимость (абсолютную или условную) знакочередующийся ряд:
1) 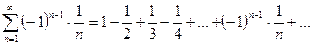 ;
;
2) 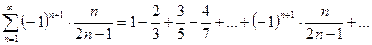 ;
;
3) 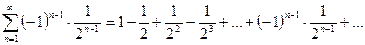 ;
;
4) 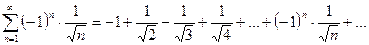 .
.
Решение: 1) Члены данного ряда по абсолютной величине монотонно убывают: 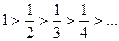 и
и 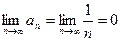 . Следовательно, согласно признаку Лейбницу, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.
. Следовательно, согласно признаку Лейбницу, ряд сходится. Выясним, сходится ли этот ряд абсолютно или условно.
Ряд 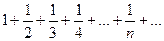 , составленный из абсолютных величин членов данного ряда, который, как, известно, расходится. Поэтому данный ряд сходится условно.
, составленный из абсолютных величин членов данного ряда, который, как, известно, расходится. Поэтому данный ряд сходится условно.
2) Члены данного ряда по абсолютной величине монотонно убывают 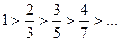 , но
, но 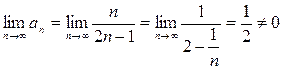 . Ряд расходится, так как признак Лейбница не выполняется.
. Ряд расходится, так как признак Лейбница не выполняется.
3) Используя признак Лейбница, получим 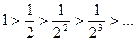 ;
; 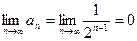 , то есть ряд сходится.
, то есть ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного ряда: 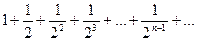 . Это геометрический ряд вида
. Это геометрический ряд вида 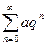
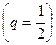 , который сходится. Поэтому данный ряд сходится абсолютно.
, который сходится. Поэтому данный ряд сходится абсолютно.
4) Используя признак Лейбница, имеем 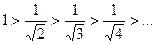 ;
; 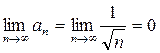 , то есть ряд сходится.
, то есть ряд сходится.
Рассмотрим ряд, составленный из абсолютных величин членов данного рада: 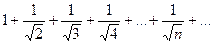 , или
, или 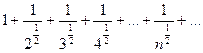 . Это обобщенный гармонический ряд, который расходится, так как
. Это обобщенный гармонический ряд, который расходится, так как 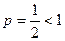 . Следовательно, данный ряд сходится условно.
. Следовательно, данный ряд сходится условно.
Задания для практической работы
1. Используя признак Лейбница, исследуйте сходимость знакочередующегося ряда:
1) 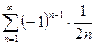 ; 2)
; 2) 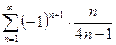 ;
;
3) 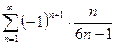 ; 4)
; 4) 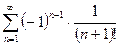 .
.
2. Исследуйте на сходимость (абсолютную или условную) знакочередующиеся ряды:
1) 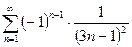 ; 2)
; 2) 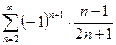 ;
;
3) 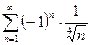 ; 4)
; 4) 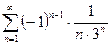 ;
;
5) 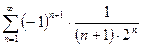 .
.
Контрольные вопросы:
1. Какой ряд называется знакопеременным?
2. Какой ряд называется знакочередующимся?
3. Сформулируйте признак Лейбница для знакочередующихся рядов.
4. Какой ряд называется абсолютно сходящимся, условно сходящимся?
5. Какие признаки используются для установления абсолютной сходимости знакопеременного ряда?
Рекомендуемая литература: 1.2[с. 405-430], 2.2[с. 66-113].
Практическая работа №24
