Тема: Составление уравнений кривых второго порядка, их построение

Цель: Формирование навыков составления уравнений кривых второго порядка, их построения

Время выполнения: 2 часа.

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Теоретический материал

Окружностью называется множество точек плоскости, равноудаленных от данной точки этой плоскости, называемой центром.

Уравнение окружности с центром в начале координат и радиусом 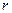имеет вид 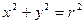. (7.1)

Уравнение окружности с центром в точке 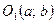и радиусом 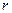имеет вид 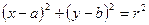. (7.2)

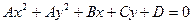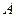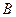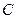Уравнение окружности в общем виде записывается так: , где , , и 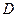- постоянные коэффициенты.

Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная 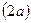, большая расстояния между фокусами .

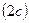Уравнение эллипса, фокусы которого лежат на оси 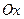, имеет вид 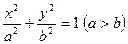, (7.3)

где 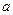- длина большей полуоси; 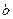- длина малой полуоси.

Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная 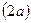, меньшая расстояния между фокусами .

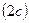Уравнение гиперболы, фокусы которого лежат на оси 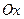, имеет вид 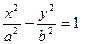, (7.4)

где 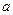- длина действительной полуоси; 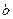- длина мнимой полуоси.

Параболой называется множество точек на плоскости, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой.

Уравнение параболы с вершиной в начале координат, осью симметрии которой служит ось 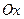и ветви направлены вверх, имеет вид 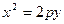, (7.5)

где 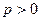(параметр параболы) – расстояние от фокуса до директрисы. Уравнение ее директрисы 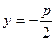. (7.6)

Задания для практической работы

1. Составьте уравнение окружности с центром в точке 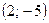и радиусом, равным 3.

2. Составьте уравнение окружности, проходящей через точк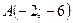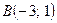и , и 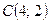. Изобразите полученную окружность в прямоугольной системе координат.

3. Составьте уравнение окружности, проходящей через точк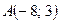и и 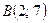, если ее центр лежит на прямой .

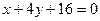4. Составьте уравнение эллипса с фокусами на оси 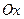, если большая ось равна 10, а эксцентриситет 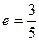. Постройте найденный эллипс в прямоугольной системе координат.

5. Составьте уравнение эллипса с фокусами на оси 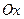, если он проходит через точк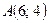и, и 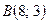. Постройте полученный эллипс в прямоугольной системе координат.

6. Дано уравнение гиперболы 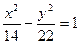. Найдите координаты фокусов и расстояние между ними.

7. Составьте уравнение гиперболы с фокусами на оси 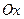, если длина ее действительной оси равна 6, а эксцентриситет равен 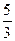. Постройте найденную гиперболу в прямоугольной системе координат.

8. Найдите точки пересечения параболы 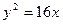с прямой 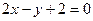. Постройте данную параболу в прямоугольной системе координат.

9. Составьте уравнение оси параболы .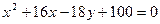

10. Составьте уравнение директрисы параболы .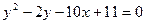

Контрольные вопросы:

1. Что называется окружностью?

2. Какой вид имеет уравнение окружности с центром в начале координат, с центром в произвольной точке?

3. Что называется эллипсом?

4. Какой вид имеет уравнение эллипса с фокусами на оси 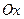, на оси ?

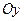5. Что называется эксцентриситетом эллипса? По какой формуле он вычисляется?

6. При помощи какого соотношения выражается зависимость между параметрами эллипса?

7. Что называется гиперболой?

8. Какой вид имеет уравнение гиперболы с фокусами на оси ?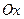

9. При помощи какого соотношения выражается зависимость между параметрами гиперболы?

10. Какая гипербола называется равносторонней? Запишите ее уравнение.

11. Что называется параболой?

12. Какой вид имеет уравнение параболы с вершиной в начале координат?

Рекомендуемая литература: 1.1[с. 309-319], 1.2[с. 304-326], 1.3[с.76-97], 2.1[с. 25-32].

СПИСОК ЛИТЕРАТУРЫ

1. Основная:

1.1 Богомолов, Н.В. Математика [Текст]: учебник для бакалавров / Н.В. Богомолов, П.И.Самойленко. - 5-е изд. - М.: Юрайт, 2014. - 396 с.

1.2 Богомолов, Н.В. Практические занятия по математике [Текст]: учебное пособие для бакалавров / Н.В. Богомолов. - 11-е изд. - М.: Юрайт, 2015. - 495 с.

1.3 Шипачев, В.С. Основы высшей математики: учебник и практикум/ В.С.Шипачев.-8-е изд. - М.: Юрайт, 2014. - 447 с.

2.Дополнительная:

2.1 Данко, П.Е., Высшая математика в упражнениях и задачах. В 2 ч. Ч.1: учеб. пособие для вузов / П.Е.Данко, А.Г. Попов, Т.Я. Кожевникова. – 8-е изд. – М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2014. – 304 с.

2.2 Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.2: Учеб. пособие для вузов / П.Е.Данко, А.Г. Попов, Т.Я. Кожевникова. – 8-е изд. – М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование»», 2014. – 416 с.

Учебное издание

ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ

Методические указания по выполнению практических работ

Составитель