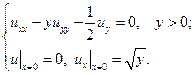II. Квазилинейные уравнения в частных производных второго порядка. Классификация и приведение к каноническому виду.

Для упрощения записи дальше будем использовать обозначения:

.

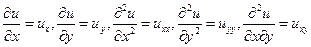Общий вид квазилинейного дифференциального уравнения второго порядка для случая, когда неизвестная функция 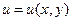зависит от двух переменных:

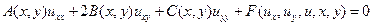. (2.1)

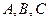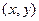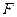Здесь функции непрерывны по , а – произвольная непрерывная по всем переменным функция. Кроме того, уравнение (2.1) невырожденное, т.е. 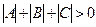. В каждой точке плоскости 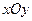уравнение вида (2.1) принадлежит к одному (и только одному) из трех типов уравнений: гиперболическому, параболическому и эллиптическому.

Тип уравнения однозначно определяется через функцию коэффициентов при старших производных :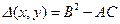

· если 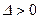, то уравнение (2.1) имеет гиперболический тип;

· если 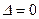, то уравнение (2.1) имеет параболический тип;

· если 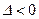, то уравнение (2.1) имеет эллиптический тип.

Функция 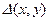сохраняет знак при любом невырожденном преобразовании координат, следовательно тип уравнения не зависит от выбора независимых переменных. Для каждого типа уравнений существует такая система координат, в которой уравнение имеет максимально простой, или, как его принято называть, канонический вид.

· Канонический вид для уравнений гиперболического типа:

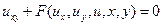или .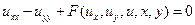

· Канонический вид для уравнений параболического типа:

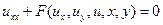или .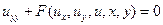

· Канонический вид для уравнений эллиптического типа:

.

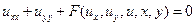Пример 2. В области 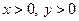провести исследование уравнения

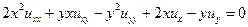: (2.2)

а) определить тип и привести уравнение к каноническому виду;

b) найти общее решение уравнения;

c) найти частное решение уравнения, удовлетворяющее условиям: , .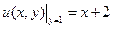

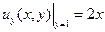Решение.

А. В указанной области 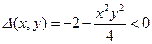, следовательно, уравнение имеет гиперболический тип. Составим уравнение характеристик

,

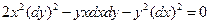распадающееся на два вещественных уравнения первого порядка, из которых находятся два первых интеграла:

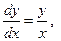• следовательно, первый интеграл ;
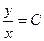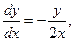• следовательно, первый интеграл .

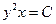Делаем замену переменных 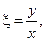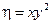, которая должна привести уравнение к канонической форме. По формулам дифференцирования сложной функции получаем:

; ;

;

;

.

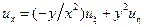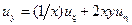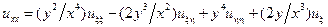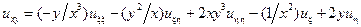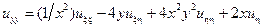Подставляя преобразованные производные в исходное уравнение и обозначая 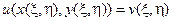, приводим его к каноническому виду:

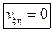. (2.3)

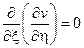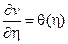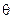В.Перепишем уравнение (2.3) в виде. Тогда , где – произвольная функция, зависящая только от .

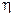Интегрируя полученное уравнение по 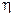, найдем, что

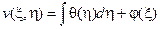или ,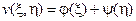

где 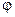, 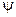– произвольные (дважды дифференцируемые) функции своих аргументов. Возвращаясь к переменным 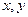получаем общее решение уравнения (2.2):

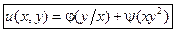. (2.4)

С.Выделим теперь из общего решения частное, т.е. найдем такие функци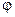и и 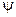, при которых выполнены заданные условия.

Из первого условия получаем: .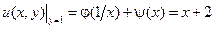

Аналогично из второго: .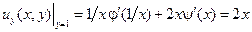

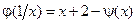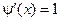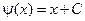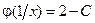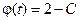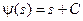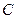Выражая из первого уравнения и подставляя во второе, получаем: , следовательно, , а . Перейдя для удобства к другим переменным, имеем окончательно: , , где – произвольная постоянная. Для получения частного решения осталось подставить найденные 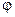и 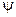в формулу (2.4): 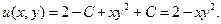Частное решение, таким образом, имеет вид:

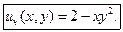
Задание 3.

В указанных областях для данных уравнений:

а) определить тип и привести уравнение к каноническому виду;

b) найти общее решение;

c) найти частное решение, удовлетворяющее заданным условиям.

1.

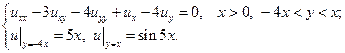
2.

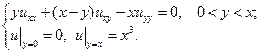
3.

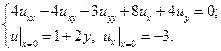
4.

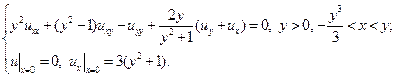
5.

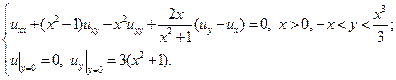
6.

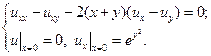
7.

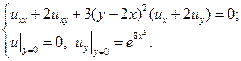
8.

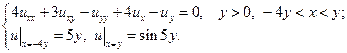
9.

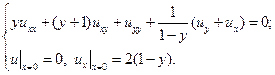
10.

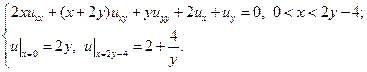
11.

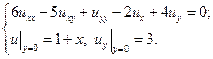
12.

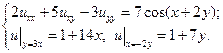
13.

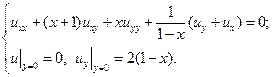
14.

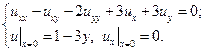
15.

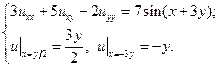
16.

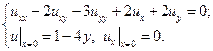
17.

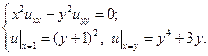
18.

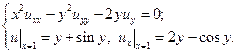
19.

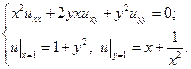
20.

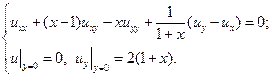
21.

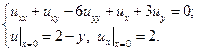
22.

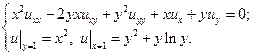
23.

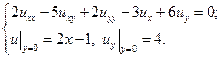
24.

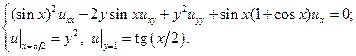
25.

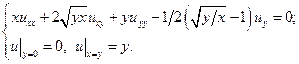
26.