Первичные параметры длинной линии
В электрических цепях с распределенными параметрами, в отличие от цепей с сосредоточенными параметрами, невозможно указать участки электрической цепи, для которых характерны те или иные процессы преобразования электромагнитной энергии: накопления энергии в магнитном или электрическом полях, преобразования энергии электрического поля в тепловую энергию. Данные процессы происходят одновременно, хотя и с различной интенсивностью, на любом бесконечно малом участке такой электрической цепи и описываются уравнениями Максвелла для дифференциальных характеристик электромагнитного поля (напряженности 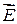 и
и 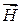 , индукции
, индукции 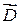 и
и 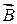 электрического и магнитного полей).
электрического и магнитного полей).
С другой стороны, для характеристики процесса распространения электромагнитной волны в электрической цепи с распределенными параметрами можно, как и для электрических цепей с сосредоточенными параметрами, использовать интегральные характеристики (величину электрических тока и напряжения). Однако в этом случае необходимо учитывать зависимость тока и напряжения не только от времени, но и от пространственных координат. Поскольку поперечными размерами длинной линии можно пренебречь по сравнению с длиной волны и, тем более, по сравнению с продольным размером, то для нее ток и напряжение будут зависеть от времени и одной координаты (условно 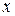 ), отсчитываемой вдоль длинной линии.
), отсчитываемой вдоль длинной линии.
Так как любому бесконечно малому участку длинной линии свойственны процессы накопления энергии в электрическом и магнитном полях, и ее рассеяния в виде тепла, то такой участок длинной линии может быть представлен следующей эквивалентной электрической схемой (рис. 1):
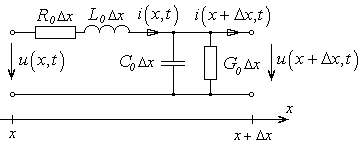
Рис. 1 – Электрическая схема замещения бесконечно малого участка длинной линии
В дальнейшем такой участок длинной линии, характеризуемый определенным значением координаты, отсчитываемой вдоль нее, будем называть сечением длинной линии с координатой 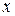 .
.
Введенные в схему параметры 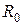 ,
, 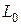 ,
, 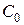 и
и 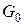 называются первичными параметрами длинной линии и имеют смысл погонных плотностей сопротивления, индуктивности, емкости и проводимости двухпроводной линии, соответственно. Первичные параметры определяются геометрией длинной линии, то есть зависят от размеров и взаимного расположения прямого и обратного токоведущих проводов длинной линии, а диссипативные параметры
называются первичными параметрами длинной линии и имеют смысл погонных плотностей сопротивления, индуктивности, емкости и проводимости двухпроводной линии, соответственно. Первичные параметры определяются геометрией длинной линии, то есть зависят от размеров и взаимного расположения прямого и обратного токоведущих проводов длинной линии, а диссипативные параметры 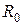 и
и 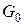 , кроме того, зависят от частоты[7]:
, кроме того, зависят от частоты[7]:
· погонное сопротивление 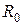 - сопротивление прямого и обратного токоведущих проводов бесконечно малого участка длинной линии, отнесенное к длине этого участка;
- сопротивление прямого и обратного токоведущих проводов бесконечно малого участка длинной линии, отнесенное к длине этого участка;
· погонная индуктивность 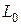 - индуктивность петли короткого замыкания из прямого и обратного токоведущих проводов бесконечно малого участка длинной линии, отнесенная к длине этого участка;
- индуктивность петли короткого замыкания из прямого и обратного токоведущих проводов бесконечно малого участка длинной линии, отнесенная к длине этого участка;
· погонная емкость 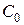 - емкость между прямым и обратным токоведущими проводами бесконечно малого участка длинной линии, отнесенная к длине этого участка;
- емкость между прямым и обратным токоведущими проводами бесконечно малого участка длинной линии, отнесенная к длине этого участка;
· погонная проводимость[8] 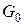 - проводимость утечки изоляции прямого и обратного токоведущих проводов бесконечно малого участка длинной линии, отнесенная к длине этого участка.
- проводимость утечки изоляции прямого и обратного токоведущих проводов бесконечно малого участка длинной линии, отнесенная к длине этого участка.
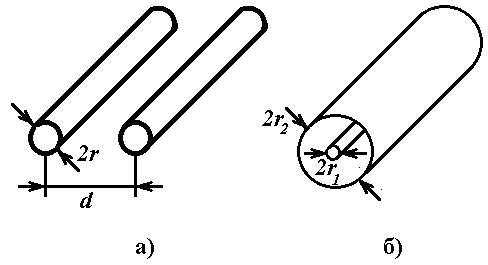
Рис. 2 – Двухпроводные длинные линии: симметричная воздушная (а) и коаксиальная (б)
Если значения первичных параметров не изменяются от сечения к сечению длинной линии, то линия называется однородной, в противном случае – неоднородной.
Если погонные сопротивление 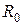 и проводимость
и проводимость 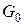 равны нулю для любого бесконечно малого участка длинной линии, то линия называется длинной линией без потерь.
равны нулю для любого бесконечно малого участка длинной линии, то линия называется длинной линией без потерь.
