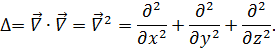Компоненты векторов в декартовой системе координат. Индексные обозначения

В декартовой системе координат компоненты вектора – это величины проекций вектора на координатные оси. Обычно координаты обозначаются 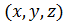, а единичные векторы, направленные вдоль осей координат (векторы базиса), – 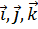. Тогда, компоненты вектора 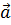будем обозначать как 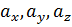. Следовательно, справедлива запись:

.

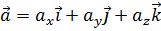Часто имеют место так называемые индексные обозначения. Координаты обозначаются как 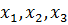(предполагается, что 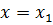, , 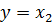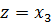). Векторы базиса при этом обозначаются 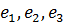, а компоненты вектора 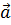- 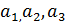. Тогда вектор 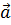можно записать в виде:

.

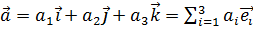Существует удобное правило для краткой записи сумм такого вида, называемое правилом Эйнштейна: если в одночленном выражении с буквенными индексами два индекса совпадают, то считается, что по этим индексам производится суммирование, а знак 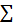опускается. Таким образом, вместо 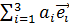, используется запись .

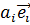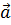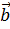Скалярным произведением двух векторов и называется число, обозначаемое 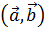и равное произведению длин векторов 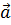, 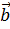и косинуса угла 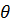между ними:

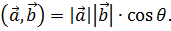
Примечание: В декартовой ортогональной системе координат скалярное произведение двух векторов равно сумме произведений их соответствующих компонент:

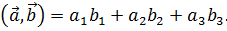
Длина вектора 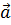определяется по формуле:

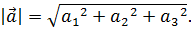
Величина проекции вектора 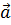на направление, задаваемое единичным вектором 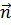, равна скалярному произведению :

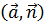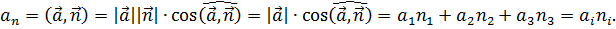
Векторным произведениемдвух векторов 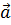и 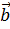называется вектор, обозначаемый 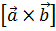иперпендикулярный векторам 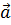и и 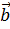направленный так, что с его конца переход от 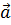к 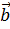происходит против часовой стрелки.

Длина этого вектора равна площади параллелограмма, построенного на векторах 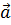и 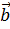. Для векторов базиса ортогональной декартовой системы координат имеем: 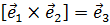, 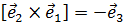и т.д. Поэтому векторное произведение в декартовой системе координат представляется в виде следующего определителя:

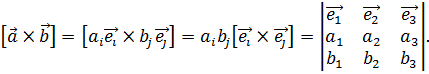
Если некоторая величина задана во всех точках рассматриваемой области, то можно говорить о поле этой величины. Например, поле скорости – это совокупность скоростей всех точек среды в рассматриваемой области.

Предположим, что в каждой точке некоторой области 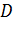нами задано значение скалярной физической величины 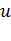, т.е. такой величины, которая полностью характеризуется своим числовым значением. Например, это может быть температура точек неравномерно нагретого тела, плотность распределения электрических зарядов в изолированном теле, потенциал электрического поля и т.д. При этом 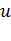называется скалярной функцией точки; записывается это так: .

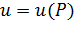Если в области 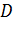задана скалярная функция точки 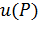, то говорят, что в этой области задано скалярное поле.

Важной характеристикой скалярного поля является скорость изменения поля в заданном направлении.

Производной функции 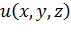по направлению в точке называется предел:

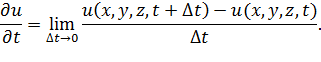
Градиент

Градиентом скалярного поля 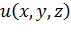называется вектор, обозначаемы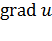й или 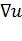, проекциями которого на оси координат служат значения частных производных :

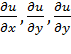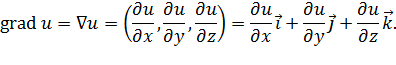
Физический смысл: Градиент функции есть вектор, направление которого указывает направление наибыстрейшего возрастания функции 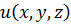, а его модуль равен наибольшей скорости изменения функции в определенной точке.

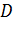Если в каждой точке области задан определенный вектор, то говорят, что в этой области задано векторное поле.

Поток вектора

Пусть векторное поле образовано вектором .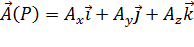

Возьмем в этом поле некоторую поверхность 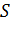и выберем на ней определенную сторону. Обозначим через 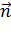единичный вектор нормали к рассматриваемой стороне поверхности в произвольной ее точке; проекциями вектора 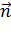служат направляющие косинусы нормали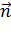 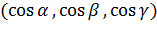. Рассмотрим интеграл по поверхности S от скалярного произведения вектора поля А(Р) на единичный вектор нормали n:

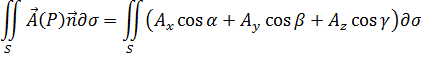		(1.1)

Если 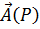– поле скоростей текущей жидкости, то интеграл (1.1) выражает поток жидкости через поверхность S. В произвольном векторном поле интеграл (1.1) будем называть потоком вектора через поверхность 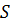и обозначим буквой .

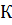Потоком вектора 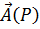через поверхность 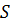называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали 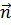к поверхности:

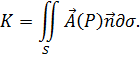
Таким образом, вычисление потока вектора сводится к вычислению интеграла по поверхности. Из определения следует, что поток вектора 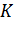– величина скалярная. Если изменить направление нормали 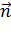на противоположное, т.е. переменить сторону поверхности 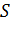, то поток 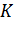изменит знак.

Особый интерес представляет случай, когда 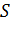– замкнутая поверхность, ограничивающая некоторую область 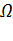. Если рассматривается внешняя нормаль, то мы будем говорить о потоке изнутри поверхности 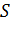. Он обозначается так:

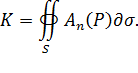
Когда векторное поле 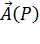представляет поле скоростей жидкости, величина потока К дает разность между количеством жидкости, вытекающей из области Ω, и количеством жидкости, поступающей в эту область.

Если 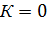, то в область 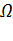жидкости втекает столько же, сколько и вытекает. Так, например, будет для любой области, расположенной в потоке воды, текущей в реке.

Если же величина 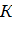отлична от 0, например, положительная, то из области 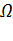жидкости вытекает больше, чем втекает. Это означает, что в области 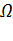имеются источники, питающие поток жидкости. Наоборот, если величина 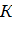отрицательна, то это указывает на наличие стоков – мест, где жидкость удаляется из потока.

Дивергенция

Рассмотрим некоторую точку 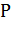векторного поля 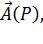находящуюся внутри области, ограниченной замкнутой поверхностью 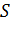, целиком содержащейся в поле. Вычислим поток вектора через поверхность 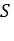и возьмем отношение этого потока к объему 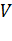области 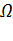, ограниченной поверхностью :

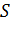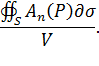
В поле скоростей жидкости это отношение определяет количество жидкости, возникающее в единицу времени в области 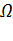, отнесенное к единице объема, т.е., как говорят, среднюю объемную мощность источника; если поток изнутри поверхности 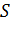меньше 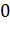, то соответственно говорят о мощности стока.

Найдем теперь предел отношения

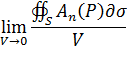
при условии, что область 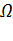стягивается в точку 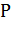, т.е., 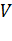стремится к .

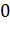Если этот предел положителен, то точка 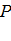называется источником, а если отрицателен, то стоком. Сама величина предела характеризует мощность источника или стока. В первом случае в любом бесконечно малом объеме, окружающем точку 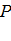, жидкость возникает, а во втором случае исчезает. Предел этот называется дивергенцией или расходимостью векторного поля в точке .

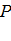Дивергенцией, или расходимостью векторного поля 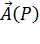в точке называется предел отношения потока вектора через поверхность, окружающую точку , к объему, ограниченному этой поверхностью, при условии, что вся поверхность стягивается в точку .

Дивергенцию поля обозначают символом 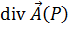. Таким образом,

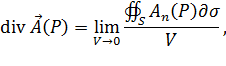
где предел вычисляется при условии, что поверхность 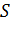стягивается к точке .

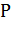Математически дивергенцию можно выразить следующим образом:

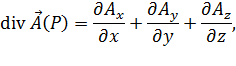
где значения частных производных берутся в точке .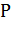

Циркуляция

Пусть векторное поле образовано вектором .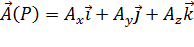

Возьмем в этом поле некоторую линию 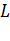и выберем на ней определенное направление. Обозначим через 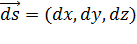вектор, имеющий направление касательной к линии и по модулю равный дифференциалу длины дуги. Направление касательной считается совпадающим с выбранным направлением на линии.

Рассмотрим криволинейный интеграл по линии 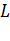от скалярного произведения векторов 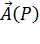и :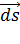

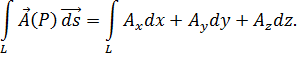		(1.2)

В силовом поле интеграл (1.2) выражает работу при перемещении материальной точки вдоль линии .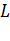

Если 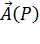– произвольное векторное поле, а 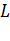– замкнутый контур, то интеграл (1.2) носит специальное название – циркуляция вектора.

Циркуляцией вектора 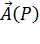вдоль замкнутого контура 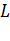называется криволинейный интеграл по этому контуру от скалярного произведения вектора 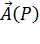на вектор 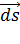касательной к контуру:

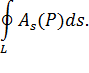
Физический смысл циркуляции вектора в случае, когда 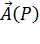– поле скоростей текущей жидкости: примем для простоты, что контур 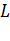- окружность, расположенная в некоторой плоскости. Предположим, что окружность является периферией колесика с радиальными лопатками, способного вращаться вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Если циркуляция будет равна 0, то колесико будет оставаться неподвижным: силы, действующие на лопатки, уравновешивают друг друга. Если циркуляция не равна 0, то колесико будет вращаться, причем тем быстрее, чем больше величина циркуляции.

Ротор

Ротором векторного поля или вихрем 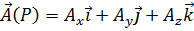называется вектор

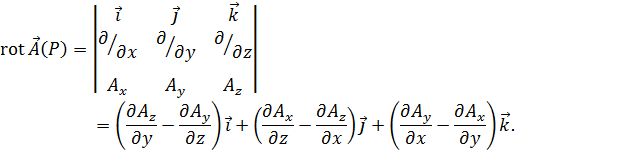
Проекция 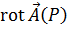этого вектора на любое направление дает предел отношения циркуляции вектора поля по контуру, лежащему в плоскости, проходящей через точку 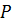, к площади, ограниченной этим контуром. Этот предел будет наибольшим в том случае, когда направление нормали 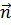совпадает с направлением .

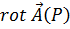Введенные нами основные понятия векторного анализа: градиент, дивергенция, ротор удобно представлять с помощью символического вектора 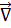(«набла-вектор»), называемого оператором Гамильтона (Гамильтонианом):

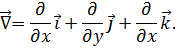
1. Произведение набла-вектора 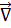на скалярную функцию 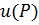дает градиент этой функции:

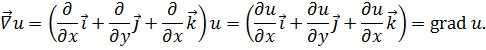
2. Скалярное произведение набла-вектора 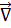на векторную функцию 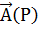дает дивергенцию этой функции:

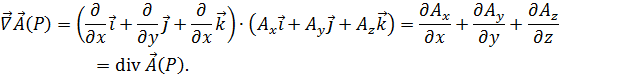
3. Векторное произведение набла-вектора 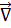на векторную функцию 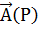дает ротор этой функции:

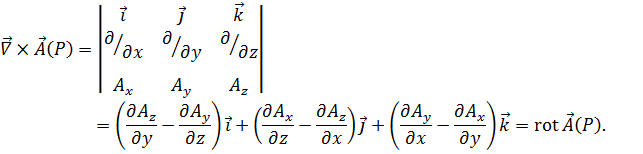
Оператор Лапласа–это оператор вида: