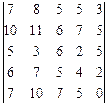Приведение определителя к треугольному виду.

Будем говорить, что определитель приведен к треугольному виду, если 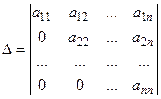. Значение такого определителя равно произведению элементов главной диагонали, то есть .

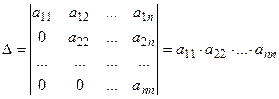Достигается такой вид определителя с помощью следующих элементарных преобразований:

- вынесение общего множителя всех элементов некоторой строки (столбца) определителя за знак определителя;

- сложение некоторой строки (столбца) определителя с другой строкой (столбцом), возможно умноженной на отличное от нуля число;

- транспозиция строк (столбцов) определителя с переменой знака определителя.

4. Разложение определителя по элементам некоторых строк (столбцов).

В основе этого метода лежит теорема Лапласа.

Сформулируем необходимые определения.

Определение. Если в определителе n-го порядка выбрать произвольно k строк и k столбцов, то элементы, стоящие на пересечении указанных строк и столбцов, образуют квадратную матрицу порядка k. Определитель такой квадратной матрицы называют минором k-го порядка. Обозначается M_k .

Если k=1, то минор первого порядка - это элемент определителя. Элементы, стоящие на пересечении оставшихся (n-k) строк и (n-k) столбцов, составляют квадратную матрицу порядка (n-k). Определитель такой матрицы называется минором, дополнительным к минору M_k (Обозначается M_n-k).

Определение. Алгебраическим дополнением минора M_k будем называть его дополнительный минор, взятый со знаком “+” или “-” в зависимости от того, четна или нечетна сумма номеров всех строк и столбцов, в которых расположен минор M_k.

Если k=1, то алгебраическое дополнение к элементу a_ik вычисляется по формуле

A_ik=(-1)^i+kM_ik, где M_ik - минор (n-1) порядка.

Теорема (Лапласа). Если в определителе n-го порядка выбрать произвольно k строк (или k столбцов), 1£k£n-1, тогда сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения равна значению определителя D.

Следствие 1. Сумма произведений элементов некоторой строки определителя на соответствующие алгебраические дополнения равна значению определителя.

Следствие 2. Сумма произведений элементов некоторой строки определителя на соответствующие алгебраические дополнения к элементам другой строки равна нулю.

Метод понижения порядка определителя.

Метод основан на следствии из теоремы Лапласа и заключается в следующем:

1. - с помощью элементарных преобразований получить в некоторой строке (столбце) определителя n-1 нулевой элемент (все, кроме одного);

2. - разложить определитель по элементам полученной строки (столбца);

3. - в результате применения следствия из теоремы Лапласа получится определитель порядка n-1 (на 1 меньше, чем порядок исходного);

4. - повторять указанные действия до тех пор, пока получится определитель третьего или второго порядка;

5. - полученный определитель вычислить одним из указанных выше способов.

Пример выполнения заданий практической части

Пример 1.Найти значение определителя, пользуясь правилом треугольника: .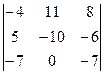

Решение.

Для вычисления значения определителя воспользуемся формулой .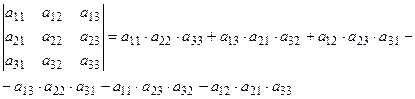

Получаем:

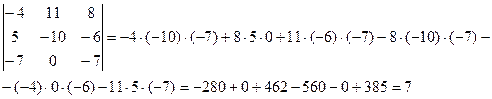
Пример 2.Найти значение определителя методом приведения к треугольному виду: .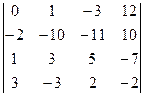

Решение.

Для приведения определителя к треугольному виду воспользуемся элементарными преобразованиями.

Сначала получим а₁₁=1.

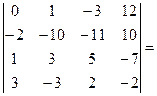[поменяем местами первый и второй столбец, поменяв при этом знак перед определителем]= – 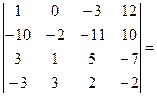[будем получать нули в первом столбце; умножим первую строку на 10 и сложим со второй] =

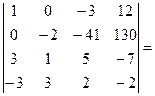= – [умножим первую строку на 3 и вычтем из третьей] =

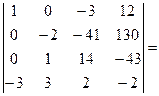= - [умножим первую строку на 3 и сложим с четвертой]=

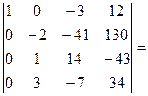= – [поменяем местами вторую и третью строки, поменяв знак перед определителем]= 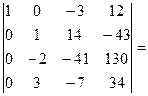[ будем получать нули во втором столбце; умножим вторую строку на 2 и сложим с третьей]= 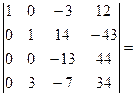[умножим вторую строку

на 3 и вычтем из четвертой]= 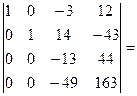[умножим третью строку на 4 и вычтем из четвертой] = 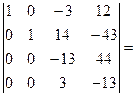[умножим четвертую строку на 4 сложим с третьей]= 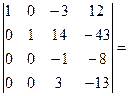[умножим третью строку на 3 и сложим с четвертой]= = 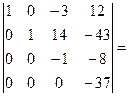[определитель приведен к треугольному виду; найдем произведение элементов главной диагонали]=37.

Пример 3.Найти значение определителя, разложив его по элементам первой и третьей строки: .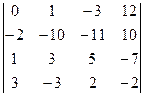

Решение.

Для вычисления значения определителя, воспользуемся теоремой Лапласа. Так как указано две строки, а данный определитель четвертого порядка, то и миноры, и их алгебраические дополнения будут являться определителями второго порядка. Получаем:

= + +

+ + +

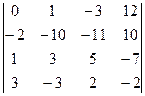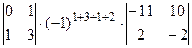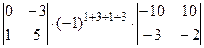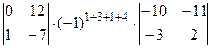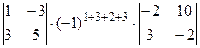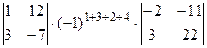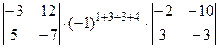+ + = (0×3-1×1) ×(-1)⁷×(-11×(-2)-10×2)+(0×5-(-3) ×1) ×(-1)⁸×(-10×(-2)-10×(-3))+(0×(-7)-12×1) ×(-1)⁹(-10×2-(-11) ×(-3))+(1×5-(-3) ×3)

×(-1)⁹×(-2×(-2)-10×3)+(1×(-7)-13×3) ×(-1)¹⁰×(-2×2-(-11) ×3)+(-3×(-7)-12×5) ×(-1)¹¹(-2×(-3)-(-10) ×3) = (-1)×(-1) ×2+3×50+(-12) ×(-1) ×(-53)+14×(-1) ×(-26)+(-43) ×29+(-39) ×(-1) ×36=37.

Пример 4.Найти значение определителя методом понижения порядка: .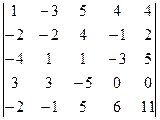

Решение.

Для того чтобы воспользоваться следствием теоремы Лапласа, получим нули, например, в первом столбце.

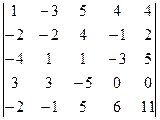=[умножим первую строку на 2 и сложим со второй]== 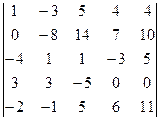=[умножим первую строку на 4 и сложим с третьей]= = 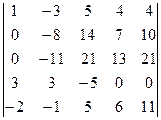=[умножим первую строку на 3 и вычтем из четвертой]= = 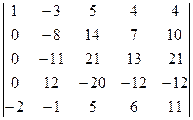=[умножим первую строку на 2 и сложим с пятой]=

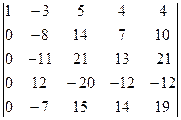= =[разложим определитель по элементам первого столбца, учитывая, что все слагаемые в разложении, кроме первого, будут равны нулю]= 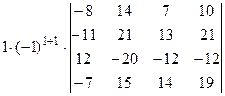=[вынесем за знак определителя из третьей строки множитель (-4)]= 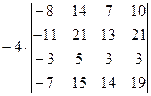=[вынесем за знак определителя из первого столбца множитель (-1)]= 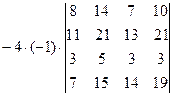=[вычтем из первой строки четвертую, чтобы получить единицу в первой строке]= 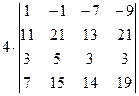=[в данном случае удобнее получать нули в первой строке, поэтому сложим первый столбец со вторым]= = 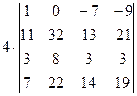=[умножим первый столбец на 7 и сложим с третьим]= = 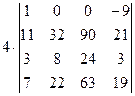=[ умножим первый столбец на 9 и сложим с четвертым]= = 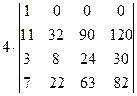=[разложим определитель по элементам первой строки, учитывая, что все слагаемые в разложении, кроме первого, будут равны нулю]=

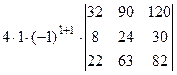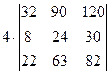= = =[вынесем из первой строки множитель 2]= = 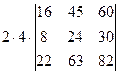= =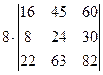[вынесем из второй строки множитель 2]= 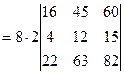=[вынесем из первого столбца множитель 2]= = 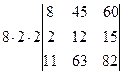= =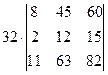[вынесем из второго столбца множитель 3]= = 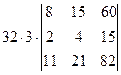=[вторую строку умножим на 4 и вычтем из первой]= = 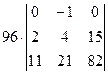=[разложим определитель по элементам первой строки, учитывая, что все слагаемые в разложении, кроме второго, будут равны нулю]= 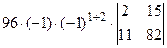=96×(2×82-11×15)=-96.

Задания для аудиторного занятия

1.Вычислить определители с помощью правила треугольников:

1.1. 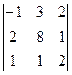; 1.2. .

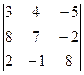2.Решить уравнения:

2.1. 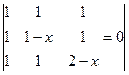; 2.2. .

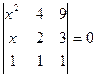3.Вычислить определитель, разложив его по элементам:

3.1. 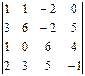4-го столбца; 3.2. 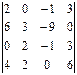3-ей строки.

4. Вычислить определители методом приведения к треугольному виду:

4.1. 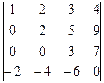; 4.2. .

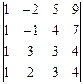5.Вычислить определители:

5.1. 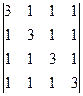; 5.2.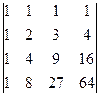

5.3. .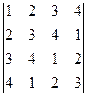

2.4. Домашнее задание

1. Вычислить определители с помощью правила треугольников:

1.1. 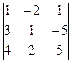; 1.2. .

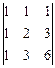2. Вычислить определитель, разложив его по элементам:

2.1. 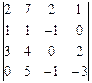4-ой строки; 2.2. 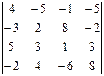3-его столбца.

3. Вычислить определители:

3.1. 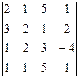; 3.2. ;

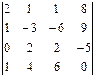3.3.