Р12. Дифференциальные уравнения
1. Уравнение 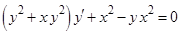 является …
является …
- уравнением Бернулли
- линейным дифференциальным уравнением первого порядка
- дифференциальным уравнением с разделяющимися переменными
- однородным относительно
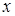 и
и 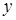 дифференциальным уравнением первого порядка
дифференциальным уравнением первого порядка
2. Дано дифференциальное уравнение 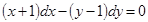 .Тогда его изоклины представляют собой…
.Тогда его изоклины представляют собой…
· пучок прямых, проходящих через одну точку
· семейство окружностей
· семейство гипербол
· семейство параллельных прямых
3. Дифференциальное уравнение 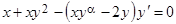 будет уравнением с разделяющимися переменными при значении
будет уравнением с разделяющимися переменными при значении 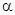 , равном …
, равном …
4. Общее решение дифференциального уравнения 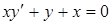 имеет вид …
имеет вид …
5. Частное решение дифференциального уравнения 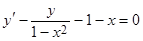 ,удовлетворяющее условию
,удовлетворяющее условию 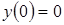 , имеет вид…
, имеет вид…
6. Общее решение линейного однородного дифференциального уравнения второго порядка 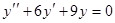 имеет вид …
имеет вид …
7. Общее решение линейного неоднородного дифференциального уравнения второго порядка 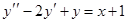 имеет вид …
имеет вид …
8. Общее решение дифференциального уравнения 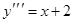 имеет вид…
имеет вид…
8.3.2. Примерные контрольные задачи в рамках учебных занятий
Входной контроль:
1. Промежуток, не содержащий ни одного решения неравенства 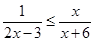 , имеет вид…
, имеет вид…
1) 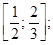 2)
2) 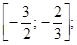 3)
3) 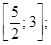 4)
4) 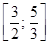 .
.
2. Число, ближайшее к корню уравнения 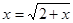 , равно…
, равно…
1) 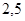 ; 2) 1; 3)
; 2) 1; 3) 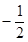 ; 4)
; 4) 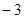 .
.
3. Сумма корней или корень (если он единственный) уравнения 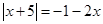 , принадлежит промежутку…
, принадлежит промежутку…
1) 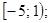 2)
2) 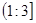 ; 3)
; 3) 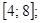 4)
4) 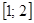 .
.
4. Решение (в градусах) уравнения 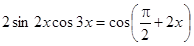 , удовлетворяющее условию
, удовлетворяющее условию 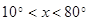 , равно …
, равно …
1) 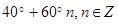 ; ; | 2) 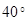 ; ; |
3) 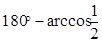 ; ; | 4) 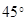 . . |
5. Область определения вида 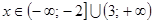 соответствует функции …
соответствует функции …
1) 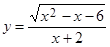 ; ; | 2) 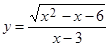 ; ; |
3) 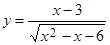 ; ; | 4) 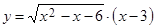 . . |
6. Отображение 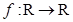 действует по правилу:
действует по правилу: 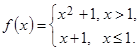 Тогда
Тогда 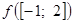 имеет вид …
имеет вид …
1) 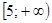 ; ; | 2) 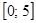 ; ; |
3) 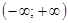 ; ; | 4) 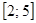 . . |
7. Область определения функции 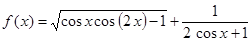 имеет вид …
имеет вид …
8. Решение неравенства 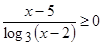 . имеет вид …
. имеет вид …
Введение в математический анализ
Контрольная работа: Последовательности (1 час)
1. Найти пределы:
1) 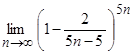 ; 2)
; 2) 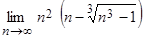 ;
;
3) 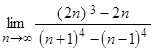 ; 4)
; 4) 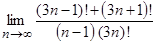 ;
;
5) 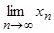 , где
, где 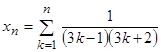 .
.
2. Доказать, пользуясь определением предела последовательности, что 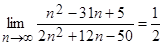 .
.
3. Используя теорему Вейерштрасса, доказать сходимость последовательности 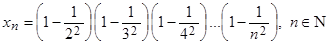 .
.
Контрольная работа: Пределы функций. Непрерывные функции (2 часа)
1. Найти пределы функций:
1.1. 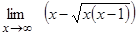 ;
;
1.2. 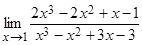 ;
;
1.3. 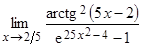 ;
;
1.4. 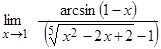 ;
;
1.5. 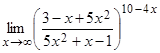 .
.
2. Исследовать функцию 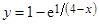 на непрерывность и построить ее график.
на непрерывность и построить ее график.
3. Применяя метод математической индукции, доказать равенство 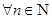
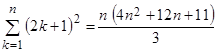 .
.
4. Найдите функцию, обратную к 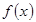 (или доказать, что таковой не существует), если
(или доказать, что таковой не существует), если 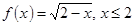 . Постройте графики прямой и обратной функций.
. Постройте графики прямой и обратной функций.
Мини-опрос на лекции Пределы функций. Непрерывные функции (20мин)
1. Свойства пределов функции в точке: теорема о единственности предела. 5 б.
2. Доказать, что 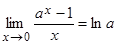 . 5 б.
. 5 б.
3. Из приведенных ниже последовательностей наименьшее значение предела при 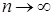 имеет последовательность
имеет последовательность
а) 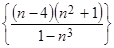 , б)
, б) 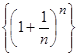 , в)
, в) 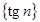 , г)
, г) 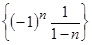 . 5 б.
. 5 б.
4. Горизонтальная асимптота графика функции 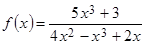 задается уравнением вида … 5 б.
задается уравнением вида … 5 б.
5. Для функции 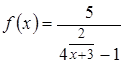 точка
точка 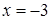 является точкой …
является точкой …
· разрыва второго рода
· непрерывности
· устранимого разрыва
· разрыва первого рода … 5 б.
6. Вертикальная асимптота графика функции 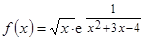 задается уравнением вида … 5 б.
задается уравнением вида … 5 б.
