Квадратные корни. Действительные числа
МАТЕМАТИКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Цели обучения.Математика как учебный предмет занимает особое место в обучении учащихся учреждений общего среднего образования. Без определенных математических знаний невозможно успешное изучение учебных предметов образовательной области «Естествознание» и других образовательных областей. Это обусловлено тем, что предметом изучения математики являются фундаментальные структуры реального мира: пространственные формы и количественные отношения — от простейших, усваиваемых в непосредственном опыте людей, до достаточно сложных, необходимых для развития научных и технологических идей.
Математика все глубже проникает в повседневную жизнь, ее идеи и методы становятся необходимыми для специалистов в различных сферах производственной и духовной деятельности. Без математических знаний невозможно понять принципы строения современной техники, научиться эффективно пользоваться ею, воспринимать и интерпретировать разнообразную социальную и экономическую информацию. Освоение математического языка способствует точному и лаконичному высказыванию мыслей.
Математика является одним из элементов общечеловеческой культуры. Ее идеи и методы оказывают большое влияние на методологию научного познания действительности. Завершенность, изящество математических формулировок, убедительная сила доказательств способствует эстетическому воспитанию учащихся.
Через деятельность на учебных занятиях по математике учащиеся усваивают общенаучные приемы и методы познания: анализ, синтез, индукцию, дедукцию, аналогию, обобщение, конкретизацию, абстрагирование.
Обучение математике, с одной стороны, приучает точно выполнять разнообразные предписания, с другой стороны, формирует общие приемы поисковой деятельности. Изучение математики вырабатывает умения выдвигать и формулировать гипотезы, искать для них обоснования или опровергать их.
Обучение математике в учреждениях общего среднего образования ставит следующие цели:
v овладение системой математических знаний, которые необходимы для применения в практической деятельности, для изучения других учебных предметов и продолжения образования;
v интеллектуальное развитие учащихся, формирование качеств мышления, характерных для деятельности не только в области математической науки, но и необходимых для полноценной жизни в обществе;
v формирование представлений о возможностях математики как науки в описании и познании действительности;
v формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса;
v воспитание таких качеств личности, как целенаправленность, настойчивость в преодолении трудностей, самостоятельность, ответственность, самоконтроль, критичность и вариативность мышления.
Организация образовательного процесса.Образовательный процесс осуществляется с учетом возрастных особенностей учащихся, специфики учебного предмета «Математика», его места и роли в структуре содержания общего среднего образования.
Организация образовательного процесса должна быть направлена на достижение учащимися результатов обучения, определенных учебными программами в соответствии с требованиями образовательного стандарта по учебному предмету «Математика» к уровню подготовки учащихся. Вместе с тем образовательный процесс должен быть поставлен так, чтобы у учащихся была возможность реализовать свои образовательные запросы. При этом необходимо, чтобы учащиеся не только усвоили определенные теоретические знания, но и научились использовать их при решении учебных задач и задач прикладного характера.
Обучение математике должно способствовать развитию у учащихся культуры устной и письменной речи, умению работать с книгой, а также формированию элементов организации умственной деятельности: планировать, ставить цели и искать пути их достижения, анализировать и оценивать результаты.
Организуя учебный процесс, учитель имеет право самостоятельно выбирать приемы и методы обучения, обеспечивающие достижение целей математического образования. При этом целесообразно обеспечивать преемственность с методами обучения на предшествующих этапах.
Постановка обучения математике должна способствовать развитию интереса к овладению знаниями, способами познания окружающего мира; созданию положительного эмоционального состояния; формированию адекватной самооценки; эстетическому воспитанию учащихся.
Структура учебного предмета «Математика».Учебный материал предмета «Математика» структурируется по семи основным содержательным линиям:
· числа и вычисления;
· выражения и их преобразования;
· уравнения и неравенства;
· координаты и функции;
· геометрические фигуры и их свойства;
· геометрические величины;
· геометрические построения.
Изучение учебного предмета «Математика» в V—XI классах осуществляется в три этапа: V—VI, VII—IX, X—XI классы.
Изучение математики на втором этапе (VII—IX классы) направлено на знакомство учащихся с действительными числами, изучение иррациональных и некоторых трансцендентных (на примере тригонометрических) выражений, уравнений и неравенств, основных элементарных функций, систематическое изучение геометрических фигур, их свойств и отношений. При изучении многочленов и рациональных дробей формируются умения осуществлять тождественные преобразования. Основным подходом к решению текстовых задач становится использование математических моделей: уравнений, неравенств, их систем.
В учебном предмете «Математика» при его изучении на втором и третьем этапах выделяется два компонента: алгебраический и геометрический.
Содержание алгебраического компонента VII—IX классов предусматривает знакомство с понятиями иррационального и действительного чисел. Введение иррациональных чисел мотивируется недостаточностью рациональных чисел для решения некоторых математических задач. Здесь систематизируются знания учащихся о выражениях и формулах; изучаются тождества, формируются навыки тождественных преобразований; рассматриваются рациональные выражения и действия над ними; изучаются квадратный трехчлен, квадратные корни и их свойства, корни степени п; свойства числовых неравенств; квадратные уравнения; линейные и квадратные неравенства; системы уравнений с двумя переменными первой степени; системы уравнений с двумя переменными, сводящиеся к уравнениям первой или второй степени; арифметическая и геометрическая прогрессии; некоторые функции, их графики и свойства (область определения, множество (область) значений, нули, промежутки знакопостоянства, возрастание, убывание, наибольшее и наименьшее значения).
Содержание геометрического компонента VII—IX классов предусматривает последовательное изучение планиметрии, включающее элементы теории параллельных прямых, треугольников, отдельных видов четырехугольников, подобия фигур, тригонометрии треугольника, знакомство с геометрическими построениями. На этом этапе продолжается формирование пространственных представлений, развитие логического мышления учащихся.
В процессе обучения на втором этапе при сочетании индуктивных и дедуктивных элементов усиливается роль теоретических обобщений и выводов. В то же время продолжается использование различных средств наглядности в качестве источника гипотез, а в отдельных случаях и для аргументации. Важно учесть, что обучение математике должно обеспечить учащимся возможность овладения математическим аппаратом, необходимым для изучения других учебных предметов.
Структура учебной программы. В учебной программе по математике для учреждений общего среднего образования выделяются разделы: «Обязательное содержание образования» и «Основные требования к результатам учебной деятельности учащихся».
В разделе «Обязательное содержание образования» указан объем учебного материала, предназначенный для обязательного изучения, который распределен по этапам обучения. Для каждого из классов указано распределение содержания по темам алгебраического и геометрического компонентов.
В разделе «Основные требования к результатам учебной деятельности учащихся»указаны результаты, которых должны достигнуть учащиеся при освоении предъявленного содержания. Основные требования к результатам учебной деятельности учащихся указаны к каждой теме
Требования к результатам учебной деятельности структурированы по компонентам: знать термины и правильно использовать понятия; знать; уметь.
VІІІ класc
Содержание учебного предмета
Алгебраический компонент
87 ч (2,5 ч в неделю)
Неравенства
Числовые неравенства, их геометрическая интерпретация.
Свойства числовых неравенств.
Линейное неравенство. Системы линейных неравенств с одной переменной.
Двойные неравенства.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• числовой промежуток; числовое неравенство; неравенство с переменной; решение неравенства; двойное неравенство; система неравенств; равносильные неравенства; модуль числа;
знать:
• что значит решить неравенство, систему неравенств; основные приемы равносильных преобразований неравенств, систем неравенств;
уметь:
• решать линейные неравенства и неравенства, сводящиеся к ним;
• решать системы линейных неравенств с одной переменной.
Квадратные уравнения
Квадратное уравнение. Формулы корней квадратного уравнения. Разложение квадратного трехчлена на линейные множители. Теорема Виета.
Квадратная (квадратичная) функция и ее график.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• квадратное уравнение, дискриминант квадратного уравнения; квадратный трехчлен; квадратная (квадратичная) функция; парабола; вершина параболы;
знать:
• формулу дискриминанта; формулы корней квадратного уравнения;
• теорему Виета; формулу разложения квадратного трехчлена на линейные множители;
уметь:
• использовать формулы корней квадратного уравнения при решении квадратных уравнений и несложных уравнений, сводящихся к ним;
• раскладывать квадратный трехчлен на множители;
• решать квадратные уравнения и уравнения, сводящиеся к ним;
• применять теорему Виета к решению задач;
• выполнять тождественные преобразования рациональных выражений, используя разложение квадратного трехчлена на линейные множители;
• строить графики квадратной (квадратичной) функции;
• использовать квадратные уравнения для решения текстовых задач.
Геометрический компонент
53 ч (1,5 ч в неделю)
Четырехугольники
Многоугольник. Сумма углов выпуклого многоугольника. Свойства и признаки параллелограмма, прямоугольника, ромба, квадрата, трапеции.
Теорема Фалеса. Деление отрезка на равные части. Свойства средней линии треугольника и трапеции.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• многоугольник; внутренний угол многоугольника; внешний угол многоугольника; вершина многоугольника; диагональ многоугольника; выпуклый многоугольник; невыпуклый многоугольник; параллелограмм; ромб; трапеция; основание трапеции; боковая сторона трапеции; высота трапеции; средняя линия трапеции; равнобедренная трапеция; прямоугольная трапеция;
знать:
• свойство углов выпуклого многоугольника;
• свойства углов параллелограмма;
• свойство сторон параллелограмма;
• свойство точки пересечения диагоналей параллелограмма;
• свойство диагоналей прямоугольника;
• свойства диагоналей ромба;
• теорему Фалеса;
• свойство средней линии треугольника;
• свойство углов трапеции, прилежащих к боковой стороне;
• свойства средней линии трапеции;
• признаки параллелограмма, прямоугольника, ромба, квадрата, трапеции;
• свойство медиан треугольника;
• свойство высот треугольника;
уметь:
• применять при решении задач основные свойства и признаки геометрических фигур.
Площадь фигур
Площадь фигуры. Площадь прямоугольника, параллелограмма, треугольника, ромба, трапеции. Теорема Пифагора.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• площадь многоугольника; равновеликие геометрические фигуры;
знать:
• формулы площади прямоугольника и параллелограмма;
• формулы площади треугольника;
• формулы площади ромба, трапеции;
• теорему Пифагора;
уметь:
• применять при решении задач основные свойства и признаки геометрических фигур.
Подобие фигур
Подобие треугольников. Коэффициент подобия. Признаки подобия треугольников. Площади подобных треугольников. Теорема Фалеса (обобщенная). Деление отрезка на пропорциональные части.
Синус, косинус, тангенс, котангенс угла от 0° до 180°. Решение прямоугольных треугольников.
Соотношения между синусом, косинусом, тангенсом, котангенсом одного угла. Формулы приведения для углов 90° ± a, 180° - a (a — острый угол).
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• пропорциональные отрезки; отношение отрезков; равные фигуры; подобные фигуры; коэффициент подобия; синус, косинус, тангенс и котангенс угла от 0° до 180°;
знать:
• определения: подобных треугольников; коэффициента подобия треугольников;
• признаки подобия треугольников;
• теорему Фалеса (обобщенную);
• свойство биссектрисы треугольника;
• свойство высоты, проведенной к гипотенузе прямоугольного треугольника;
• свойство площадей подобных треугольников;
• значения sin a, cos a при a, равном 0°, 30°, 45°, 60°, 90°, 180°;
• значения tg a, ctg a при a, равном 30°, 45°, 60°;
• свойства периметров и площадей подобных фигур;
уметь:
• применять: теоремы к решению задач на вычисление и доказательство; свойства подобных треугольников к решению задач на построение.
Контрольные работы 8 (8 ч)
IX класс
Алгебраический компонент
(2,5 ч в неделю, всего 87 ч)
Функции
Функция. Область определения и множество (область) значений функции. Способы задания функции. График функции. Возрастание и убывание функции. Наибольшее и наименьшее значения функции. Нули функции. Промежутки знакопостоянства функции.
Функции у =  , y =
, y = 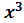 , y =
, y = 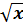 , их свойства и графики.
, их свойства и графики.
основные Требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
функция; аргумент функции; значение функции; область определения функции; множество (область) значений функции, график функции; четность и нечетность функции; наибольшее и наименьшее значения функции; нули функции; промежуток возрастания функции, промежуток убывания функции; промежуток возрастания функции, промежуток убывания функции, промежуток знакопостоянства;
знать: свойства функций у =  , y =
, y = 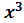 , y =
, y = 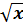 ;
;
уметь: находить область определения функции, определять по графику функции ее свойства;
строить графики у =  , y =
, y = 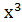 , y =
, y = 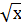 .
.
МАТЕМАТИКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Цели обучения.Математика как учебный предмет занимает особое место в обучении учащихся учреждений общего среднего образования. Без определенных математических знаний невозможно успешное изучение учебных предметов образовательной области «Естествознание» и других образовательных областей. Это обусловлено тем, что предметом изучения математики являются фундаментальные структуры реального мира: пространственные формы и количественные отношения — от простейших, усваиваемых в непосредственном опыте людей, до достаточно сложных, необходимых для развития научных и технологических идей.
Математика все глубже проникает в повседневную жизнь, ее идеи и методы становятся необходимыми для специалистов в различных сферах производственной и духовной деятельности. Без математических знаний невозможно понять принципы строения современной техники, научиться эффективно пользоваться ею, воспринимать и интерпретировать разнообразную социальную и экономическую информацию. Освоение математического языка способствует точному и лаконичному высказыванию мыслей.
Математика является одним из элементов общечеловеческой культуры. Ее идеи и методы оказывают большое влияние на методологию научного познания действительности. Завершенность, изящество математических формулировок, убедительная сила доказательств способствует эстетическому воспитанию учащихся.
Через деятельность на учебных занятиях по математике учащиеся усваивают общенаучные приемы и методы познания: анализ, синтез, индукцию, дедукцию, аналогию, обобщение, конкретизацию, абстрагирование.
Обучение математике, с одной стороны, приучает точно выполнять разнообразные предписания, с другой стороны, формирует общие приемы поисковой деятельности. Изучение математики вырабатывает умения выдвигать и формулировать гипотезы, искать для них обоснования или опровергать их.
Обучение математике в учреждениях общего среднего образования ставит следующие цели:
v овладение системой математических знаний, которые необходимы для применения в практической деятельности, для изучения других учебных предметов и продолжения образования;
v интеллектуальное развитие учащихся, формирование качеств мышления, характерных для деятельности не только в области математической науки, но и необходимых для полноценной жизни в обществе;
v формирование представлений о возможностях математики как науки в описании и познании действительности;
v формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса;
v воспитание таких качеств личности, как целенаправленность, настойчивость в преодолении трудностей, самостоятельность, ответственность, самоконтроль, критичность и вариативность мышления.
Организация образовательного процесса.Образовательный процесс осуществляется с учетом возрастных особенностей учащихся, специфики учебного предмета «Математика», его места и роли в структуре содержания общего среднего образования.
Организация образовательного процесса должна быть направлена на достижение учащимися результатов обучения, определенных учебными программами в соответствии с требованиями образовательного стандарта по учебному предмету «Математика» к уровню подготовки учащихся. Вместе с тем образовательный процесс должен быть поставлен так, чтобы у учащихся была возможность реализовать свои образовательные запросы. При этом необходимо, чтобы учащиеся не только усвоили определенные теоретические знания, но и научились использовать их при решении учебных задач и задач прикладного характера.
Обучение математике должно способствовать развитию у учащихся культуры устной и письменной речи, умению работать с книгой, а также формированию элементов организации умственной деятельности: планировать, ставить цели и искать пути их достижения, анализировать и оценивать результаты.
Организуя учебный процесс, учитель имеет право самостоятельно выбирать приемы и методы обучения, обеспечивающие достижение целей математического образования. При этом целесообразно обеспечивать преемственность с методами обучения на предшествующих этапах.
Постановка обучения математике должна способствовать развитию интереса к овладению знаниями, способами познания окружающего мира; созданию положительного эмоционального состояния; формированию адекватной самооценки; эстетическому воспитанию учащихся.
Структура учебного предмета «Математика».Учебный материал предмета «Математика» структурируется по семи основным содержательным линиям:
· числа и вычисления;
· выражения и их преобразования;
· уравнения и неравенства;
· координаты и функции;
· геометрические фигуры и их свойства;
· геометрические величины;
· геометрические построения.
Изучение учебного предмета «Математика» в V—XI классах осуществляется в три этапа: V—VI, VII—IX, X—XI классы.
Изучение математики на втором этапе (VII—IX классы) направлено на знакомство учащихся с действительными числами, изучение иррациональных и некоторых трансцендентных (на примере тригонометрических) выражений, уравнений и неравенств, основных элементарных функций, систематическое изучение геометрических фигур, их свойств и отношений. При изучении многочленов и рациональных дробей формируются умения осуществлять тождественные преобразования. Основным подходом к решению текстовых задач становится использование математических моделей: уравнений, неравенств, их систем.
В учебном предмете «Математика» при его изучении на втором и третьем этапах выделяется два компонента: алгебраический и геометрический.
Содержание алгебраического компонента VII—IX классов предусматривает знакомство с понятиями иррационального и действительного чисел. Введение иррациональных чисел мотивируется недостаточностью рациональных чисел для решения некоторых математических задач. Здесь систематизируются знания учащихся о выражениях и формулах; изучаются тождества, формируются навыки тождественных преобразований; рассматриваются рациональные выражения и действия над ними; изучаются квадратный трехчлен, квадратные корни и их свойства, корни степени п; свойства числовых неравенств; квадратные уравнения; линейные и квадратные неравенства; системы уравнений с двумя переменными первой степени; системы уравнений с двумя переменными, сводящиеся к уравнениям первой или второй степени; арифметическая и геометрическая прогрессии; некоторые функции, их графики и свойства (область определения, множество (область) значений, нули, промежутки знакопостоянства, возрастание, убывание, наибольшее и наименьшее значения).
Содержание геометрического компонента VII—IX классов предусматривает последовательное изучение планиметрии, включающее элементы теории параллельных прямых, треугольников, отдельных видов четырехугольников, подобия фигур, тригонометрии треугольника, знакомство с геометрическими построениями. На этом этапе продолжается формирование пространственных представлений, развитие логического мышления учащихся.
В процессе обучения на втором этапе при сочетании индуктивных и дедуктивных элементов усиливается роль теоретических обобщений и выводов. В то же время продолжается использование различных средств наглядности в качестве источника гипотез, а в отдельных случаях и для аргументации. Важно учесть, что обучение математике должно обеспечить учащимся возможность овладения математическим аппаратом, необходимым для изучения других учебных предметов.
Структура учебной программы. В учебной программе по математике для учреждений общего среднего образования выделяются разделы: «Обязательное содержание образования» и «Основные требования к результатам учебной деятельности учащихся».
В разделе «Обязательное содержание образования» указан объем учебного материала, предназначенный для обязательного изучения, который распределен по этапам обучения. Для каждого из классов указано распределение содержания по темам алгебраического и геометрического компонентов.
В разделе «Основные требования к результатам учебной деятельности учащихся»указаны результаты, которых должны достигнуть учащиеся при освоении предъявленного содержания. Основные требования к результатам учебной деятельности учащихся указаны к каждой теме
Требования к результатам учебной деятельности структурированы по компонентам: знать термины и правильно использовать понятия; знать; уметь.
VІІІ класc
Содержание учебного предмета
Алгебраический компонент
87 ч (2,5 ч в неделю)
Неравенства
Числовые неравенства, их геометрическая интерпретация.
Свойства числовых неравенств.
Линейное неравенство. Системы линейных неравенств с одной переменной.
Двойные неравенства.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• числовой промежуток; числовое неравенство; неравенство с переменной; решение неравенства; двойное неравенство; система неравенств; равносильные неравенства; модуль числа;
знать:
• что значит решить неравенство, систему неравенств; основные приемы равносильных преобразований неравенств, систем неравенств;
уметь:
• решать линейные неравенства и неравенства, сводящиеся к ним;
• решать системы линейных неравенств с одной переменной.
Квадратные корни. Действительные числа
Корень n-й степени из числа.
Иррациональное число. Действительное число. Сравнение действительных чисел.
Числовые промежутки.
Арифметический квадратный корень и его свойства.
Основные требования к результатам учебной деятельностиучащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• корень n-й степени из числа, подкоренное выражение, степень корня, квадратный корень из числа; арифметический квадратный корень из числа; рациональное число, конечная десятичная дробь; бесконечная периодическая десятичная дробь; бесконечная непериодическая десятичная дробь; иррациональное число, действительное число;
знать:
• определение и свойства квадратных корней;
• как называются и обозначаются основные числовые множества;
• представление: рационального числа в виде бесконечной десятичной периодической дроби; иррационального числа в виде бесконечной десятичной непериодической дроби;
уметь:
• читать и записывать числовые промежутки;
• выполнять с использованием свойств квадратных корней тождественные преобразования несложных иррациональных выражений, включая вынесение множителя из-под знака корня и внесение множителя под знак корня.
Квадратные уравнения
Квадратное уравнение. Формулы корней квадратного уравнения. Разложение квадратного трехчлена на линейные множители. Теорема Виета.
Квадратная (квадратичная) функция и ее график.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• квадратное уравнение, дискриминант квадратного уравнения; квадратный трехчлен; квадратная (квадратичная) функция; парабола; вершина параболы;
знать:
• формулу дискриминанта; формулы корней квадратного уравнения;
• теорему Виета; формулу разложения квадратного трехчлена на линейные множители;
уметь:
• использовать формулы корней квадратного уравнения при решении квадратных уравнений и несложных уравнений, сводящихся к ним;
• раскладывать квадратный трехчлен на множители;
• решать квадратные уравнения и уравнения, сводящиеся к ним;
• применять теорему Виета к решению задач;
• выполнять тождественные преобразования рациональных выражений, используя разложение квадратного трехчлена на линейные множители;
• строить графики квадратной (квадратичной) функции;
• использовать квадратные уравнения для решения текстовых задач.
Геометрический компонент
53 ч (1,5 ч в неделю)
Четырехугольники
Многоугольник. Сумма углов выпуклого многоугольника. Свойства и признаки параллелограмма, прямоугольника, ромба, квадрата, трапеции.
Теорема Фалеса. Деление отрезка на равные части. Свойства средней линии треугольника и трапеции.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• многоугольник; внутренний угол многоугольника; внешний угол многоугольника; вершина многоугольника; диагональ многоугольника; выпуклый многоугольник; невыпуклый многоугольник; параллелограмм; ромб; трапеция; основание трапеции; боковая сторона трапеции; высота трапеции; средняя линия трапеции; равнобедренная трапеция; прямоугольная трапеция;
знать:
• свойство углов выпуклого многоугольника;
• свойства углов параллелограмма;
• свойство сторон параллелограмма;
• свойство точки пересечения диагоналей параллелограмма;
• свойство диагоналей прямоугольника;
• свойства диагоналей ромба;
• теорему Фалеса;
• свойство средней линии треугольника;
• свойство углов трапеции, прилежащих к боковой стороне;
• свойства средней линии трапеции;
• признаки параллелограмма, прямоугольника, ромба, квадрата, трапеции;
• свойство медиан треугольника;
• свойство высот треугольника;
уметь:
• применять при решении задач основные свойства и признаки геометрических фигур.
Площадь фигур
Площадь фигуры. Площадь прямоугольника, параллелограмма, треугольника, ромба, трапеции. Теорема Пифагора.
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• площадь многоугольника; равновеликие геометрические фигуры;
знать:
• формулы площади прямоугольника и параллелограмма;
• формулы площади треугольника;
• формулы площади ромба, трапеции;
• теорему Пифагора;
уметь:
• применять при решении задач основные свойства и признаки геометрических фигур.
Подобие фигур
Подобие треугольников. Коэффициент подобия. Признаки подобия треугольников. Площади подобных треугольников. Теорема Фалеса (обобщенная). Деление отрезка на пропорциональные части.
Синус, косинус, тангенс, котангенс угла от 0° до 180°. Решение прямоугольных треугольников.
Соотношения между синусом, косинусом, тангенсом, котангенсом одного угла. Формулы приведения для углов 90° ± a, 180° - a (a — острый угол).
Основные требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
• пропорциональные отрезки; отношение отрезков; равные фигуры; подобные фигуры; коэффициент подобия; синус, косинус, тангенс и котангенс угла от 0° до 180°;
знать:
• определения: подобных треугольников; коэффициента подобия треугольников;
• признаки подобия треугольников;
• теорему Фалеса (обобщенную);
• свойство биссектрисы треугольника;
• свойство высоты, проведенной к гипотенузе прямоугольного треугольника;
• свойство площадей подобных треугольников;
• значения sin a, cos a при a, равном 0°, 30°, 45°, 60°, 90°, 180°;
• значения tg a, ctg a при a, равном 30°, 45°, 60°;
• свойства периметров и площадей подобных фигур;
уметь:
• применять: теоремы к решению задач на вычисление и доказательство; свойства подобных треугольников к решению задач на построение.
Контрольные работы 8 (8 ч)
IX класс
Алгебраический компонент
(2,5 ч в неделю, всего 87 ч)
Функции
Функция. Область определения и множество (область) значений функции. Способы задания функции. График функции. Возрастание и убывание функции. Наибольшее и наименьшее значения функции. Нули функции. Промежутки знакопостоянства функции.
Функции у =  , y =
, y = 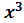 , y =
, y = 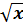 , их свойства и графики.
, их свойства и графики.
основные Требования к результатам учебной деятельности учащихся
Учащиеся должны:
знать термины и правильно использовать понятия:
функция; аргумент функции; значение функции; область определения функции; множество (область) значений функции, график функции; четность и нечетность функции; наибольшее и наименьшее значения функции; нули функции; промежуток возрастания функции, промежуток убывания функции; промежуток возрастания функции, промежуток убывания функции, промежуток знакопостоянства;
знать: свойства функций у =  , y =
, y = 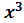 , y =
, y = 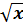 ;
;
уметь: находить область определения функции, определять по графику функции ее свойства;
строить графики у =  , y =
, y = 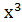 , y =
, y = 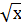 .
.
