Решение задач свободной конвекции

Движение жидкости в системе под действием неоднородного поля сил, приложенных к частицам внутри системы и обусловленных внешними полями, называют свободным движением или свободной (естественной) конвекцией. Перенос теплоты, происходящий при обтекании твердого тела потоком жидкости при ее свободном движении, называют теплоотдачей при свободном движении жидкостиили теплоотдачей при свободной конвекции.

Расчетные формулы, полученные аналитически для ламинарного пограничного слоя, при свободной конвекции не всегда точно совпадают с экспериментальными данными. Например, при малых значениях чисел Грасгофа (Gr < 10⁴) результаты, полученные по формулам, не совпадают с экспериментальными данными, так как толщина пограничного слоя слишком велика по отношению к размерам тела и уровня пограничного слоя оказываются непригодными для описания реальной физической обстановки. В этом случае необходимо решать полную систему дифференциальных уравнений Навье-Стокса, неразрывности и энергии. Однако эта задача весьма трудоемка. Следует отметить, что теплоотдача в условиях турбулентного пограничного слоя при Gr > 10⁹ не может быть решена аналитически, так как механизм переноса теплоты окончательно не установлен.

Многие задачи свободной конвекции в неограниченном пространстве решены экспериментально. Проведены исследования с воздухом, водородом, углекислотой, водой, анилином, глицерином, четыреххлористым углеродом, различными маслами и др. (во всех случаях Pr > 0,7).

Теплоотдача в указанных жидкостях определялась для тел различной формы и размеров (диаметр проволок и труб изменялся от 0,015 до 245 мм, диаметр шаров от 30 мм до 16 м, высота пластин и труб от 0,25 до 6 м).

Теплоотдача в газах измерялась при различных давлениях от 0,003 до 7 МПа.

Характерным размером при свободной конвекции считается проекция теплопередающей поверхности на вертикальную плоскость.

Определяющей температурой при свободной конвекции является средняя температура пограничного слоя:

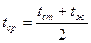, (13.1)

где t_ж - температура среды (теплоносителя) за пределами пограничного слоя; t_ст - температура поверхности.

Михеев М.А. обобщил результаты перечисленных экспериментальных измерений и предложил следующую расчетную формулу:

Nu_m = с(Gr^.Pr)_mⁿ. (13.2)

Физические константы в этой формуле определяются по средней температуре пограничного слоя.

Значения коэффициентов с и n определяются в зависимости от произведения (Gr^.Pr) и приведены в таблице 13.1.

Таблица 13.1 - Значения коэффициентов с и n

Gr.Pr	1.10-3...5.102	5.102...2.107	2.107...1.1013
c	1,18	0,54	0,135
n	1/8	1/4	1/3

При Gr^.Pr = 1^.10^-3...5^.10² - теплоотдача слабо зависит от произведения Gr^.Pr и теплота переносится в основном вследствие теплопроводности.

При Gr^.Pr = 5^.10²...2^.10⁷ существует ламинарный пограничный слой и теплота переносится в основном вследствие свободной конвекции при ламинарном режиме движения жидкости.

При Gr^.Pr = 2^.10⁷...1^.10¹³ теплота переносится вследствие свободной конвекции при турбулентном движении жидкости.

Далее, определив коэффициент теплоотдачи 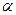по формуле (13.3), используют уравнение Ньютона-Рихмана (13.4) для нахождения удельного теплового потока.

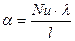. (13.3)

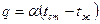. (13.4)