Методы теории подобия и теплового моделирования

Значение критериев подобия очень важно при использовании теории подобия физических процессов. Они являются мерой или признаком подобия. Возьмем два геометрически подобных канала, в которых протекают различные жидкости с разными скоростями. Гидродинамические явления будут подобны друг другу, если для любых сходственных точек пространства будет соблюдаться пропорциональность скоростей и физических свойств жидкостей – плотности 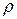и вязкости 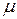, т.е. .

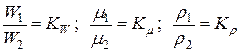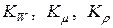- константы или множители подобия. В случае конвективной теплоотдачи для теплового подобия двух потоков, протекающих в каналах необходимо, кроме соблюдения геометрического подобия, также соблюдение полей скоростей и физических свойств жидкостей, кроме того, подобие температурных полей. Таким образом, физические процессы будут подобными, во-первых, если они одинаковы по своей природе, т.е. качественно одинаковы и описываются одними и теми же математическими уравнениями; во-вторых, если процессы протекают в геометрически подобных устройствах и в-третьих, если поля всех одноименных физических величин соответственно будут подобны.

Критерии, составленные из условий однозначности, называются определяющими. Если критерий содержит искомую величину, то его называют неопределяющим.

При моделировании изучение процесса в образце заменяется исследованием этого же процесса на модели. Очевидно, процесс в модели должен быть осуществлен так, чтобы результаты его изучения можно было перенести на образец. Условия моделирования, т. е. условия, которым должна удовлетворять модель и протекающий в ней процесс, дает теория подобия. Если процесс в модели будет подобен процессу в образце, то результаты исследования на модели могут быть применены к образцу. Моделирование по существу включает в себя две самостоятельные задачи. Во-первых, в модели необходимо осуществить процесс, подобный процессу, происходящему в образце, и, во-вторых, выполнить на модели все требуемые измерения и наблюдения. Мы рассматриваем первую задачу. Условия однозначности для стационарных процессов состоят:

1. из геометрических условий, характеризующих форму и размеры тела, в котором протекает процесс;

2. из физических условий, характеризующих физические свойства рассматриваемой среды;

3. из граничных условий, характеризующих особенности протекания процесса на границах жидкости.

Таким образом, необходимо осуществить геометрическое подобие образца и модели. Все размеры образца и модели, существенные для процесса конвективного теплообмена, должны быть связаны между собой соотношением 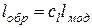, т. е. модель должна быть построена как точная копия образца, уменьшенная в 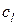раз. Конечно, копироваться должна не внешняя форма образца, а внутренняя конфигурация каналов, по которым движутся газы или жидкости. Обычно геометрическое подобие осуществить нетрудно. Следует только иметь в виду, что изменение геометрических размеров не должно привести к качественному изменению процесса в модели и, следовательно, к нарушению первого условия подобия.

При моделировании необходимо также осуществить подобие процессов на границах исследуемой жидкости. Чаще всего это условие ограничивается требованием подобия условий входа жидкости в образец и модель (чтобы обеспечить подобное распределение скоростей на входе) и требованием подобия температурных полей на входе в аппарате и на поверхности тел, участвующих в теплообмене. Подобия условий входа жидкости можно достичь путем устройства входного участка модели геометрически подобным входному участку образца. Если температура жидкости на входе в образец не меняется по сечению канала, условие подобия температурных полей на входе выдержать нетрудно. Для этого достаточно, чтобы в канале, подводящем жидкость или газ к модели, не было теплообмена. Если же температурное поле на входе имеет сложный характер, то осуществить в модели такое распределение температур труднее.

Выполнение точного подобия процессов конвективного теплообмена и, следовательно, проведение точного моделирования, этих процессов часто наталкивается на непреодолимые трудности. В связи с этим возникает необходимость в разработке методов приближенного моделирования. Одной из возможностей приближенного моделирования является проявление так называемой автомодельности процесса относительно какого-либо критерия. Говорят, что определяемая величина автомодельна относительно критерия подобия, если она не зависит от него. Если процесс автомоделен относительно какого-либо критерия подобия, то при моделировании отпадает необходимость соблюдать равенство этого критерия для образца и модели. Явление автомодельности дает возможность упрощения дифференциальных уравнений и условий однозначности. Члены уравнений (или условий однозначности), учитывающие факторы, относительно которых процесс оказывается автомодельным, могут быть опущены или видоизменены.
Ввиду трудности точного моделирования на практике часто используется приближенный метод локального теплового моделирования. Особенность этого метода заключается в том, что подобие процессов стараются осуществить лишь в том месте, где производится исследование теплоотдачи. Например, если изучается теплоотдача при омывании жидкостью пучка труб, то в опытах в теплообмене может участвовать только одна из труб. Остальные трубы служат только для придания модели формы, подобной образцу. Данные о теплоотдаче получают из измерений, проведенных на единичной трубе. Предполагается, что теплоотдача испытуемой трубы в основном зависит от характера ее омывания, определяемого расположением системы труб, а не тепловыми условиями. Метод локального моделирования сравнительно прост и в ряде случаев позволяет получать достаточно точные результаты.