Дифференциальное уравнение теплопроводности
Решение задач теплопроводности связано с определением поля температур и тепловых потоков. Для установления зависимости между величинами, характеризующими явление теплопроводности, воспользуемся методом математической физики, который рассматривает протекание физических процессов в произвольно выделенном из всего рассматриваемого пространства элементарном объеме и в течение бесконечно малого промежутка времени. Это позволяет пренебречь изменением некоторых величин и существенно упростить выкладки.
При выводе дифференциального уравнения теплопроводности считаем, что тело однородно и изотропно (то есть физические свойства тела не зависят от выбранного в нём направления), физические параметры l, с (теплоемкость), и r (плотность) постоянны, внутренние источники теплоты равномерно распределены в теле. Под внутренними источниками теплоты понимаются тепловыделения, например, в тепловыделяющих элементах атомных реакторов, или при прохождении тока в электрических проводниках. Внутренние источники теплоты характеризуются величиной qv — количеством теплоты, которое выделяется в единице объема в единицу времени.
В основу вывода положен закон сохранения энергии, согласно которому вся теплота, выделенная внутренними источниками dQвн и внесенная извне в элементарный объем путем теплопроводности dQm за время dt, идет на изменение внутренней энергии вещества, содержащегося в этом объеме:
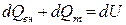 (10.7)
(10.7)
Выделим в теле элементарный параллелепипед с ребрами dx, dy, dz (рис. 10.2).
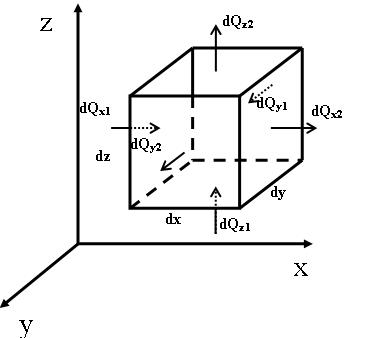
Рисунок 10.2– К выводу дифференциального уравнения теплопроводности
Количество теплоты, которое проходит путем теплопроводности внутрь выделенного объема в направлении оси Ох через элементарную площадку dy×dz за время dt:
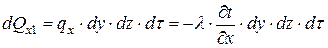 (10. 8)
(10. 8)
На противоположной грани параллелепипеда температура получит приращение 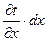 и будет составлять
и будет составлять 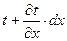 Количество тепла, отведенного через эту грань:
Количество тепла, отведенного через эту грань:
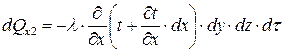
Разница количества теплоты, подведенного к элементарному параллелепипеду и отведенного от него, представляет собой теплоту, внесенную путем теплопроводности в направлении оси Ох:
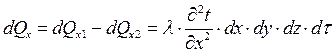 .
.
Аналогично:
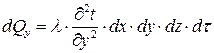 ;
;
Полное количество теплоты внесено в элементарный параллелепипед путем теплопроводности:
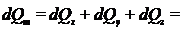
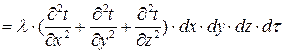 .
.
Здесь произведение dx×dy×dz представляет собой объем элементарного параллелепипеда dv. Количество теплоты, которое выделилось в элементарном объеме за счет внутренних источников:
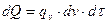 .
.
Приращение внутренней энергии можно выразить через массу параллелепипеда r×dv, теплоемкость с и приращение температуры 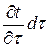 :
:
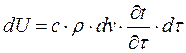 .
.
Подставляя выражения для dQm, dQвн и dU в уравнение (107.), после соответствующих сокращений получаем:
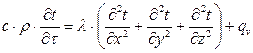 (10.9)
(10.9)
Сумма вторых частных производных любой функции в математическом анализе носит название оператора Лапласа и обозначается следующим образом:
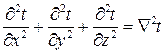 .
.
Величину 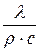 называют коэффициентом температуропроводности и обозначают буквой
называют коэффициентом температуропроводности и обозначают буквой 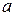 . В указанных обозначениях уравнение (10.9) примет вид:
. В указанных обозначениях уравнение (10.9) примет вид:
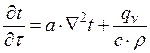 . (10.10)
. (10.10)
Это уравнение называется дифференциальным уравнением теплопроводности или уравнением Фурье и лежит в основе математической теории теплопроводности. Коэффициент температуропроводности 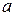 является физическим параметром вещества. Из уравнения (10.10) следует, что изменение температуры во времени для любой точки тела пропорционально величине
является физическим параметром вещества. Из уравнения (10.10) следует, что изменение температуры во времени для любой точки тела пропорционально величине 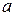 .
.
