Дифференциальное уравнение теплопроводности с источником теплоты

При выводе уравнения теплопроводности (3.32) предполагалось отсутствие внутренних источников или стоков теплоты. Однако есть среды, внутри которых могут протекать те или иные процессы с выделением (источник) или поглощением (сток) теплоты. К таким средам, относятся вода, лед, снег, пар, а также металлы, бетон, химические и другие вещества. Процесс испарения воды, таяния льда и снега сопровождается поглощением теплоты, а обратный ему процесс — замерзание воды — выделением теплоты. При этом теплота источника или стока может зависеть не только от координат тела, но и от его температуры и ее распределения в теле.

При наличии источника или стока уравнение теплового баланса (3.27) должно быть дополнено еще одним членом, учитывающим их теплоту, а именно:

Q₈ = W dxdydzdτ, (3.40)

где Q₈ — количество теплоты, выделенное или поглощенное средой в объеме ¶x¶y¶z за время dτ; W — интенсивность источника или стока.

С учетом дополнительного члена (3.40) уравнение теплопроводности (3.32) запишем в следующем виде:

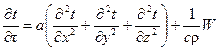
(3.41)

или

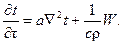(3.42)

В том случае, когда в среде имеют место поглотители (сток) тепловой энергии, перед вторым слагаемым правой части уравнения следует ставить знак минус.

Условия однозначности

Полученное выше дифференциальное уравнение теплопроводности описывает явление передачи теплоты в самом общем виде. Чтобы решить с помощью этого уравнения конкретную задачу, отличающуюся какими-либо условиями от сотни других задач, необходимо сформулировать для нее еще и так называемые условия однозначности – совокупность всех условий, которыми задача однозначно определяется (само уравнение теплопроводности или теплового баланса в них не входит).

Условия однозначности состоят:

1) из геометрических условий, характеризующих форму и размеры тела или системы тел, в которых протекает тепловой процесс;

2) из физических условий, характеризующих физические свойства рассматриваемой среды и тела;

3) из временных условий, характеризующих распределение температуры в рассматриваемой среде или теле в начальный момент времени. По этой причине эти условия называют еще и начальными условиями;

4) из граничных условий, характеризующих взаимодействие рассматриваемого тела с окружающей его средой.

Совокупность последних двух условий (начальных и граничных) называется краевыми условиями, так как первые находятся на начальном «краю» времени, а вторые – на геометрических «краях» тела.

Начальные условия заключаются в задании распределения поля значений температуры в начальный момент времени (τ=0), т.е. предшествующий расчетному. Они должны быть заданы в виде функций:

1) t_{τ = 0} = f₁ (x, у, z) - для пространственной задачи,

2) t_{τ = 0} = f₂ (x, у) - для плоской задачи,

3) t_{τ = 0} = f₃ (x) - для линейной задачи.

В большинстве случаев эти условия могут быть заданы с достаточной определенностью в виде конкретной функции, таблицы или в форме графика (например, распределение температуры по толщине слоя воды).

Граничные условия – тепловые условия у поверхности тела, которые задаются в более сложном виде. При решении задач теплопроводности принято различать четыре наиболее часто встречающихся способа задания граничных условий, так называемые граничные условия первого, второго, третьего, четвертого и пятого рода.

1. Граничные условия первого рода заключаются в том, что задается температура во всех точках поверхности тела в течение времени τ:

t_п = f₄ (X, Y, Z, τ), (3.43)

где X, Y, Z — координаты поверхности.

2. Если количество теплоты, поступающей извне в тело, известно (или задано), то такое граничное условие называют граничным условием второго рода и оно заключается в том, что задается удельный тепловой поток по закону Фурье через поверхность тела в течение времени τ:

q_п = - λ ¶t/¶n. (3.44)

Как и в предыдущем случае, эта функция может быть произвольной и непрерывной:

q_п = f₅ (X, Y, Z, τ). (3.45)

3. Граничные условия третьего рода заключаются в задании температуры поверхности тела и окружающей его среды и задании теплообмена (коэффициента теплопередачи) между поверхностью этого тела и окружающей средой по закону Ньютона. Таким образом, количество теплоты, отдаваемое (или получаемое) единицей поверхности с температурой t_п за единицу времени в окружающую среду с температурой t_с, прямо пропорционально разности температуры поверхности и окружающей среды:

q_п = a (t_п - t_с). (3.46)

Количество теплоты, отдаваемое (или получаемое) поверхностью в окружающую среду и определяемое по формуле (3.46), должно быть равно количеству теплоты, подводимому к этой поверхности за счет теплопроводности, которое определяется по закону Фурье (3.44). Приравняв эти потоки, получим новое выражение для задания граничных условий третьего рода:

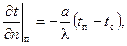
(3.47)

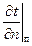где — градиент температуры у поверхности и по нормали к ней.

В условии (3.47) должны быть заданы коэффициент теплоотдачи a и температура окружающей тело среды t_с.

4. Граничные условия четвертого рода заключаются в том, что задается равенство температуры на поверхности раздела двух тел или тела с окружающей средой при подходе к ней с двух сторон, а также удельных тепловых потоков по закону Фурье в предположении, что между этими телами осуществляется идеальный контакт.

5. При наличии на поверхности тела слоя, имеющего очень высокую теплопроводность, например, слоя ветрового перемешивания в водохранилище, и заданного количества теплоты, поступающего в слой извне, имеем граничное условие пятого рода.

Практически важным является граничное условие четвертого рода при наличии на границе источника (стока) теплоты, возникающего от изменения агрегатного состояния, например, при промерзании грунта.

Возможны и некоторые другие граничные условия; так, часто встречается совмещение граничных условий второго и третьего родов, которое производится путем замены действительной температуры окружающей среды эквивалентным значением.

Методы решения задач

Для решения задачи о распределении температуры в пределах заданного поля и в расчетный период времени с помощью полученных выше уравнений помимо краевых условий необходимо располагать методом решения этих уравнений.

За 175 лет со времени выхода в свет «Аналитической теории тепла» — классической работы Фурье, теория теплообмена обогатилась рядом таких методов. Первый из них был предложен самим Фурье и известен как «решения в рядах Фурье».

Все эти методы могут быть распределены по следующим группам: аналитические, конечных разностей (графический, численный), исследования температурных полей на моделях (физический), аналоговых и счетных машин.

К настоящему времени наиболее разработаны методы решения уравнения теплопроводности для одномерных задач, как раз тех задач, с которыми преимущественно имеют дело гидрологи и гидротехники.

Аналитические методы решения уравнения теплопроводности состоят в том, что, пользуясь полной математической формулировкой задачи, находят ее аналитическое решение. При этом следует искать уже готовое решение, а не новое. Для этого необходимо обратиться, прежде всего, к монографиям Г.Карслоу и Д.Егер, А. В. Лыкова и др., в которых приведен набор решений различных задач. При отсутствии готового решения целесообразно попытаться найти его в виде суммы (комбинации) имеющихся решений, пользуясь известным принципом суперпозиции. Достоинством этих методов является точность решений; она зависит лишь от точности закладываемых исходных данных и точности производимых вычислений. При решении задачи возможно использование ЭВМ. Температура рассчитывается для любой точки тела и для любого момента времени независимо от расчетов за предшествующие интервалы времени. Недостатком является ограниченность круга задач, для которых могут быть получены решения.

Метод конечных разностей состоит в том, что в дифференциальном уравнении теплопроводности, которое следует решить, все бесконечно малые разности (дифференциалы) заменяются конечными, но малыми разностными величинами. Следовательно, истинное непрерывное в пространстве распределение температуры и непрерывный во времени ход температуры заменяется приближенными прерывистыми значениями, осредняющими температуру конечных малых участков тела ∆x, ∆y, ∆z и малых промежутков времени ∆τ. Достоинством метода является возможность решить весьма сложные задачи, в том числе для тел сложной формы. Метод позволяет использование ЭВМ. К недостаткам метода относятся: отсутствие общего решения задачи; необходимость производства вычислений для всего тела и для всего периода, предшествующего моменту времени, для которого производится вычисление температуры; трудоемкость метода.

Метод исследования температурных полей на моделях (физическое моделирование) является экспериментальным методом решения теплотехнических задач. Он опирается на теорию подобия и применяется в тех случаях, когда аналитические и другие методы не могут дать ответ. Суть метода состоит в том, что исследование процессов и явлений, протекающих в изучаемом объекте, заменяется исследованием их протекания на его модели. Данные, полученные на модели, позволяют судить о тех же процессах и явлениях, протекающих на объекте. Существенным достоинством данного метода является возможность решения сложных задач и исследования недоступных объектов.

Метод аналоговых и счетных машин (метод аналогий) состоит в том, что решение тепловой задачи заменяют уже имеющимся решением задачи другой физической сущности, в которой уравнения и краевые условия совпадают с первой задачей, хотя размерности у них различны (метод ЭТА).