Дифференциальное уравнение теплопроводности
Для решения практических задач по переносу тепла теплопроводностью помимо закона Фурье необходимо знать распределение температур в пространстве и во времени, так как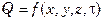 
.
С этой целью в однородном и изотропном твердом теле выделяется бесконечно малый прямоугольный параллелепипед с гранями dx, dy, dz и постоянной плотностью r, удельной теплоемкостью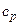 
и коэффициентом теплопроводности l. Поток тепла, проходящий через этот параллелепипед (рис. 7.2), можно разложить на три составляющие в направлениях осей координат.
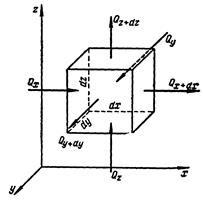 Рисунок 7.2 – К выводу дифференциального уравнения теплопроводности |
Согласно закону Фурье в направлении оси x за промежуток времени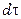 
к грани dydz параллелепипеда подводится количество тепла.
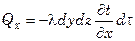. (7.17)
Через противоположную грань параллелепипеда, находящуюся на расстоянии dx, выходит в направлении оси х тепло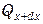 
:
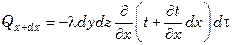, (7.18)
либо
,
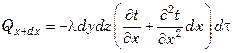так как температура на противоположной грани равна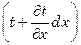 
.
Следовательно, изменение количества тепла (приращение или убыль) в параллелепипеде по направлению оси х составит:
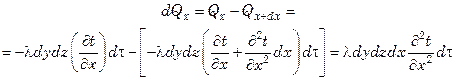(7.19)
либо
,
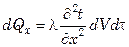где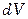 
– объем параллелепипеда.
Аналогично выразятся изменения количеств тепла в параллелепипеде по направлению осей у и z:
; 
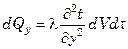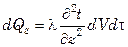. (7.20)
Полное изменение тепла в объеме параллелепипеда составит:
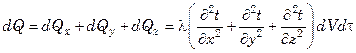. (7.21)
Поток тепла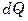 
приводит к изменению температуры параллелепипеда на величину 
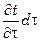, что влечет за собой изменение теплосодержания параллелепипеда за время :
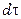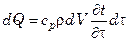. (7.22)
Из уравнений (7.21) и (7.22) следует:
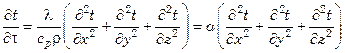, (7.23)
либо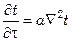 
.
Здесь множитель a – коэффициент температуропроводности (см. подразд. 7.2).
Полученное уравнение (7.23) является дифференциальным уравнением теплопроводности Фурье, представляющим распределение температур во времени и пространстве при неустановившемся процессе.
При установившемся процессе теплопроводности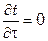 
, тогда
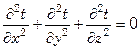. (7.24)
Таким образом, дифференциальное уравнение теплопроводности дает возможность решать задачи как при установившемся, так и при неустановившемся тепловом потоке.
Однако (7.23) и (7.24) определяют передачу тепла теплопроводностью в самом общем виде, без учета формы тела, через которое проводится тепло, его свойств и свойств окружающей среды. При решении конкретных задач эти уравнения дополняются условиями однозначности или краевыми условиями.
Условия однозначности включают в себя:
1) геометрические параметры, характеризующие форму и линейные размеры тела, в котором протекает процесс;
2) физические параметры, описывающие физические свойства среды и тела (λ, с,ρи т.д.);
3) временные или начальные условия, характеризуют распределение температур в рассматриваемом теле в начальный момент времени;
4) граничные условия, описывающие взаимодействие данного тела с окружающей средой.
Начальные условиянеобходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае этот закон может быть записан в виде: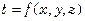 
, так как 
.
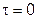При равномерном распределении температуры в теле при ,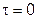 
.
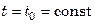Граничные условия могут быть заданы несколькими способами.
1. Задается распределение температуры по поверхности тела для каждого момента времени (граничные условия первого рода):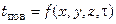 
.
В частном случае, когда температура на поверхности является постоянной на протяжении всего времени протекания процесса теплообмена, последняя зависимость упрощается до вида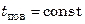 
.
2. Задаются значения теплового потока для каждой точки поверхности тела в любой момент времени (граничные условия второго рода). Аналитически это можно представить таким образом: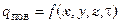 
, где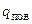 
– плотность теплового потока на поверхности тела.
В простейшем случае плотность теплового потока на поверхности и во времени остается постоянной: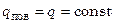 
.
3. Задаются температура окружающей среды tср и закон теплообмена между поверхностью тела и окружающей средой (граничные условия третьего рода). Это граничное условие характеризует закон теплообмена между поверхностью и окружающей средой в процессе охлаждения и нагревания тела.
Процесс теплообмена между поверхностью тела и средой относится к очень сложным процессам и зависит от большого количества параметров. Подробно эти вопросы будут рассмотрены в дальнейшем.
Дифференциальное уравнение теплопроводности (7.23) с заданными условиями однозначности дает полное математическое описание краевой задачи теплопроводности. Поставленная таким образом задача разрешается аналитическим, численным или экспериментальным методом. В случае экспериментального решения задач теплопроводности используют методы физического или математического моделирования.
В инженерной практике часто приходится решать задачи стационарной теплопроводности через плоскую, цилиндрическую и сферическую стенки. К этим задачам, в частности, относится расчет тепловой изоляции аппаратов и трубопроводов.