Исследование взаимосвязей качественных показателей.

Качественные показатели (признаки) – это показатели, которые нельзя изменить, но с помощью которых можно сравнивать объекты между собой по степени улучшения или ухудшения этого показателя, то есть ранжировать (упорядочивать) объекты. Для оценки тесноты связей качественных признаков используются следующие показатели.

Коэффициент ассоциации ( 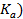. Он применяется для оценки тесноты связи между двумя альтернативными показателями (признаками).

Пусть провели n наблюдений за двумя признаками А и Б и получили таблицу результатов (n= ):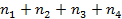

Таблица 2

Таблица результатов

Признак Б	Признак А
да	нет
Да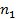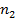
Нет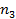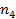

Для оценки тесноты связи между такими показателями вычисляют коэффициент ассоциации :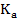

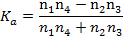
При этом -1 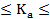+1. Чем больше значение 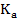по модулю, тем теснее связь между показателями. При 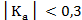связь между показателями практически отсутствует.

Коэффициент контингенции ( 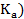, характеризующий тесноту связи между двумя альтернативными показателями, вычисляется по формуле:

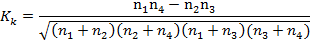
Коэффициент контингенции изменяется в диапазоне -1 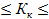+1. При 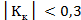связь между показателями практически отсутствует.

Пример. Из 82 студентов специальности, проживающих в общежитии, научно-исследовательской работой занимаются 54. Из 169 студентов специальности, не проживающих в общежитии, НИР занимаются 65 человек. Имеется ли взаимосвязь между проживанием в общежитии и занятием научно-исследовательской работой?

Решение. Вычислим коэффициент ассоциации и коэффициент контингенции для имеющихся данных.

Имеем: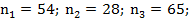

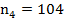
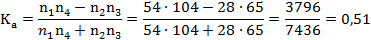
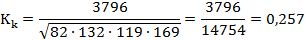
Вывод: наблюдается средняя положительная корреляция между проживанием в общежитии и занятием НИР.

Ранговые коэффициенты Спирмена и Кендалла оценивают степень тесноты связи между двумя ранговыми (качественными, порядковыми) показателями.

Пусть имеем n объектов, которые характеризуются двумя качественными показателями A и B. Проранжируем объекты в порядке ухудшения качества по показателю А и присвоим объектам ранги 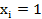. Затем при данном расположении объектов пропишем ранг 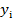по признаку B. Тогда ранговый коэффициент корреляции Спирмена вычисляется по формуле:

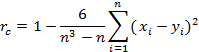
Допустим, что справа от 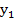имеется 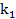рангов больше, чем 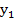, а справа от 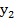- 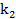рангов больше, чем 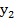,….., справа от 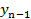- 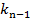рангов больше, чем 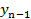. Тогда ранговый коэффициент корреляции Кендалла вычисляется по формуле:

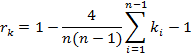
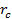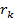Оба коэффициента по модулю меньше единицы и при больших n межу значениями и наблюдается определенное соотношение 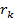/ 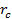=2/3

Проверка гипотезы о значимости выборочного коэффициента ранговой корреляции Спирмена ( 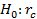=0) осуществляется с использованием T – критерия Стьюдента.

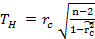
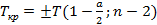
Проверка гипотезы о значимости выборочного коэффициента ранговой корреляции Кендалла ( 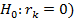осуществляется использованием критерия, приводящего к нормальному закону распределения.

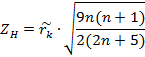
Пример. На конкурсе инвестиционных проектов 11 участников получили следующие оценки (по стобальной системе) за экологичность (экологическую безопасность) и экономическую обоснованность расчетов:

№ проекта
Экологичность
Экономическая обоснованность

Связаны ли между собой экологичность и экономическая обоснованность расчетов?

Решение. Тесноту связи между экологичностью и экономической обоснованностью расчетов определим с помощью ранговых коэффициентов корреляции. Ранжируем участников конкурса:

№ участника
Ранг за экологичность,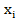
Ранг за экон. обосн.,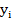

Вычислим ранговый коэффициент Спирмена:

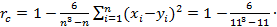
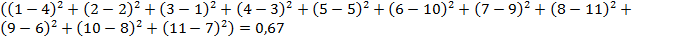
Справа от 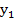имеется 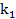=7 рангов больших, чем 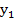, справа от 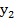имеется 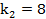больших, чем 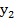. Аналогично находим:

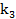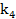=8, =7, , , , ,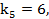

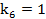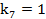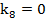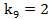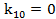
Вычислим ранговый коэффициент Кендалла:

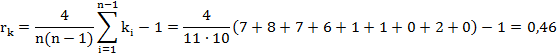
Оценим значимость вычисленных коэффициентов Спирмена и Кендалла при уровнях значимости a=0,01, a=0,05, a=0,1

Проверка гипотезы о значимости коэффициента ранговой корреляции Спирмена ( 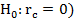осуществляется с использованием T – критерия Стьюдента.

Вычислим наблюдаемое значение критерия:

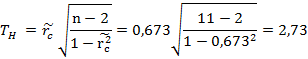
Для различных уровней значимости по таблице квантилей T – критерия Стьюдента найдем критические точки.

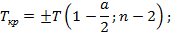
При а=001 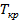=T( ;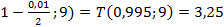

При а=005 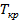=T( ;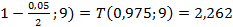

При а=0,10 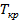=T( ;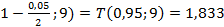

При уровнях значимости a=0,05 и а=0,1 данные противоречат гипотезе о незначимости коэффициента Спирмена, то есть между экологичностью и экономической обоснованностью есть связь, а при уровне значимости а=0,01 нет оснований отвергать гипотезу, то есть полученный коэффициент незначим.

Проверим значимость коэффициента ранговой корреляции Кендалла ( 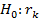=0). Вычислим наблюдаемое значение критерия:

Для различных уровней значимости с помощью табличной функции Лапласа найдем критические точки.

;

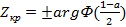При а=0,01 ;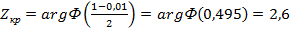

При а=0,05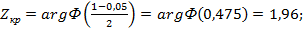

При а=0,10 ;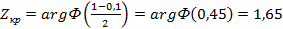

При уровнях значимости а=0,05 и а=0,1 данные противоречат гипотезе о незначимости коэффициента Кендалла, то есть между экологичностью и экономической обоснованностью расчетов есть связь (это характеризует качество всего проекта), а при уровне значимости а=0,01 нет оснований отвергать гипотезу и полученный коэффициент незначим.

Коэффициент конкордации – характеристика связи между несколькими признаками, измеряемыми в порядковой (ранговой) шкале.

Пусть имеется выборка объема m из генеральной совокупности объема n. X=( 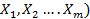, признаки (показатели) , которой можно измерить в порядковой шкале.

Имеем 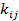– ранги i-того наблюдения (члена) вариационного ряда j-того признака (j=1,2…..n; j=1,2…..m).

Если при ранжировании имеются совпадающие наблюдения, например, подряд в вариационном ряду идут l одинаковых значений признака 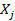, то вместо обычных рангов, определяемых в вариационном ряду, приписывают каждому из этих одинаковых значений одно и то же число, равное средней арифметической их рангов.

Такие полученные ранги называют объединенными или связными, и они могут быть дробными.

Например, имеется ряд величин себестоимости продукции 2,5; 3.0; 8.5; 9.0; 9.0; 9.0; 9.5; 9.5; 9.6; 9.6. Ранги этих значений будут следующие: 1; 2; 3; 5; 5; 5; 7.5; 7.5; 9.5; 9.5.

Коэффициент конкордации (согласованности) вычисляется по формуле:

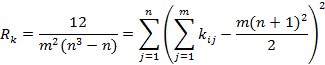
Для связных рангов вычисления производят по формуле:

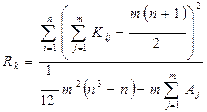
где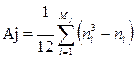

Здесь n_l - число неразличимых элементов (рангов) в l-й группе признака X _j ; M _j,— число таких групп из неразличимых рангов.

Коэффициент конкордации заключен в пределах от 0 до 1.

При R_k <0.3 связь между показателями практически отсутствует.

Для проверки гипотезы о значимости коэффициента конкордации (H₀ : R_K = О) вычисляют 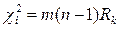исравнивают полученное зна­чение с величиной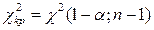

Пример. Группа из 5 экспертов оценивает качество однотипной продукции, выпускаемой на 7 предприятиях.

Предпочтения экспертов (их ранги) представлены в таблице:

Эксперт	Предприятия эедприятия

Взаимосвязаны (согласуются) ли мнения экспертов? Рассчитать коэффициент конкордации и оценить его значимость.

Решение. Вычислим коэффициент конкордации по формуле:

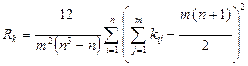
где n = 7 - объем выборки; m = 5 - количество ранговых показателей (экспертов).

Промежуточные расчёты представлены в таблице:

Расчетные	Предприятия
величины								Итого
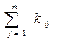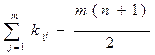	- 12	- 11

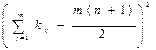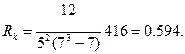
Значимость коэффициента конкордации (H₀ : R_k = 0) проверяется по

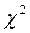- распределению.

Вычислим наблюдаемое значение критерия:

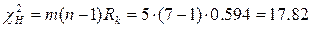
Критическое значение 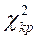найдем по таблице квантилей 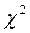- распределения по заданному уровню значимости 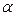и числу степеней свободы v = п - 1.

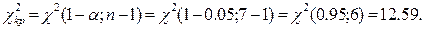Так как 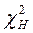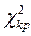^> , то гипотезу H₀ отвергаем, то есть коэффициент конкордации R_k значим. Значит, мнения экспертов по оценки качества выпускаемой продукции на предприятиях согласуются.

Дисперсионный анализ