Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
Рассмотрим линейное неоднородное уравнение с постоянными коэффициентами
у(n) + p1 у(n-1) + p2 у(n-2) + … + pn-1 у´ + pn у = q(x), (19)
где p1, p2, … , pn – некоторые постоянные.
Его частное решение можно получить методом вариации произвольных постоянных. Однако, когда правая часть уравнения (19) имеет так называемый специальный вид, частное решение находится проще.
1. Если q(x) = eαxPm(x), где Pm(x) – многочлен m–й степени, то частное решение следует искать в
виде участн = xs eαxQm(x),
где Qm(x) – многочлен m–й степени с неопределенными коэффициентами; s = 0, если α не является корнем характеристического уравнения; если же α является корнем характеристического уравнения, то s равно кратности этого корня.
2. Если q(x) = eαx (Ui (x) cosβx + Wj (x) sinβx), где Ui (x), Wj (x) – многочлены степени i и j, тогда
частное решение следует искать в виде
участн = xs eαx [Rk (x) cosβx + Tk (x) sinβx],
где Rk (x), Tk (x) – многочлены k–й степени (k = max {i, j}) с неопределенными коэффициентами; s = 0, если α + iβ не является корнем характеристического уравнения; если же α + iβ – корень характеристического уравнения, то s – его кратность.
ЗАДАЧИ
1. Решить дифференциальные уравнения:
1.1. y´´ +3у´ = 18x + 9.
Р е ш е н и е. Характеристическое уравнение: λ2+3λ = 0. Его корни λ 1= 0, λ 2= –3.
Так как α = 0 – корень характеристического уравнения кратности 1, то частное решение ищем в виде
участн = x (Ax + B).
Подставим его в уравнение
2A + 3(2Ax + B) = 18x + 9.
Приравняем коэффициенты при одинаковых степенях х:
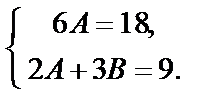
Отсюда А = 3, В = 1 и
участн = 3х2 + х .
Общее решение неоднородного уравнения
уобщ = С1е-3х + С2 + 3х2 + х .
1.2. y´´´ – 6у´´ + 9у´ = x е3х.
Р е ш е н и е. Характеристическое уравнение: λ3– 6λ2+9λ = 0 ó λ ( λ2– 6λ +9 ) = λ ( λ – 3 ) 2. Его
корни λ 1= 0, λ 2= 3, λ 3= 3.
Так как λ = 3 – корень кратности 2, то частное решение ищем в виде
участн = x2 (Ax + B) е3х.
Подсчитаем производные (для краткости опустим индекс частн) :
y = x2 (Ax + B) е3х.
y´ = 2x (Ax + B) е3х + Ax2 е3х + 3x2 (Ax + B) е3х = е3х (2Ax2 + 2Bx + x2 + 3Ax3 + 3Bx2) = е3х (3Ax3 + 3Ax2+ 3Bx2 + 2Bx).
y´´ = 3е3х (3Ax3 + 3Ax2+3Bx2 + 3Bx2 + 2Bx) + е3х (9Ax2 + 6Ax + 6Bx +2B ) = е3х (9Ax3 +18Ax2 + 9Bx2 + 6Ax + 12Bx +2B ).
y´´´ = 3е3х (9Ax3 +18Ax2 + 9Bx2 + 6Ax + 12Bx +2B ) + е3х (27Ax2 +36Ax + 18Bx + 6A + 12B) =
= е3х (27Ax3 +81Ax2 + 27Bx2 + 54Ax + 54Bx + 6A +18B ) .
Подставим их в уравнение:
е3х (27Ax3 +81Ax2 + 27Bx2 + 54Ax + 54Bx + 6A +18B ) – 6 е3х (9Ax3 +18Ax2 + 9Bx2 + 6Ax + 12Bx +2B ) + 9 е3х (3Ax3 + 3Ax2+ + 3Bx2 + 2Bx) = х е3х .
Сокращаем левую и правую части на е3х и приводим подобные члены. Имеем:
0·Ax3 +0·Ax2 + 0·Bx2 + (18A + 0·B) x + 6A + 6B = x => 0·x3 + 0·x2 + 18A·x + (6A + 6B).= x
Приравняем коэффициенты при одинаковых степенях х:
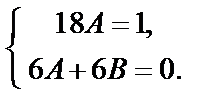
Отсюда А = 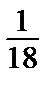 , В = –
, В = – 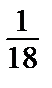 и
и
участн = 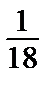 (х3 – х2) е3х .
(х3 – х2) е3х .
Общее решение неоднородного уравнения
уобщ = С1 + С2 е3х + С3 x е3х + 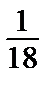 (х3 – х2) е3х.
(х3 – х2) е3х.
1.3. y´´ +2у´ + y = cos x.
Р е ш е н и е. Характеристическое уравнение: λ2+2λ + 1 = 0. Его корни λ 1= λ 2= –1.
Правую часть можно записать так: cos x = e0·x (1 · cos x + 0 · sin x) Так как α = 0 не является корнем
характеристического уравнения, то частное решение ищем в виде
участн = A cos x + B sin x.
Подсчитаем производные (для краткости опустим индекс частн) :
у = A cos x + B sin x.
y´ = – A sin x + B cos x,
y´´ = – A cos x – B sin x,
Подставим их в уравнение
– A cos x – B sin x + 2(– A sin x + B cos x) + A cos x + B sin x = cos.
Приравняем коэффициенты при одинаковых степенях cos x и sin x в левой и правой частях уравнения:
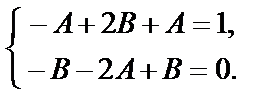 или
или 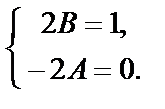
Отсюда А = 0, В = 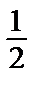 и
и
участн = 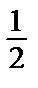 sin x.
sin x.
Общее решение неоднородного уравнения уобщ = С1е-х + С2 х е-х + 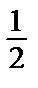 sin x.
sin x.
1.4. y´´ + у = 4хех.
1.5. y´´ + у = 4 sin x.
1.6. y´´ – 2у´ – 3у = е4х.
1.7. y´´ + 2у´ – 3у = x2 ех.
1.8. y´´ + 4у´ + 4у = x е2х.
1.9. y´´ – у = 2 ех – x2.
1.10. y´´´ + у´´ = 6x + е–х.
1.11. y´´´´ + 5у´´ + 4у = 3sin x.
2. Записать ожидаемый вид частного решения уравнения
2.1. у′′ + 3у′ = –2 + (2 – х) е –х + 3sin x + 5x2.
Р е ш е н и е. Правая часть представляет собой сумму трех функций специального вида: f1(x) = 5x2 – 2,
f2(x) = (2 – х) е –х, f3(x) = 3sin x. Характеристическое уравнение k2 + 3k = 0 имеет корни k1 = 0, k2 = –3. Следовательно,
для f1(x) ожидаемый вид частного решения уч1 = х ∙ (ax2 + bx + c), т.к. f1(x) = е0 ∙ x (5x2 – 2). Здесь 5x2 – 2 – полином 2-й степени. Умножаем на х потому, что 0 является корнем характеристического уравнения;
для f2(x) ожидаемый вид частного решения уч2 = е –х (dx + g);
для f3(x) = 3sin x = е0 ∙ x (0 ∙ cos x + 3sin x) ожидаемый вид частного решения уч3 = u cos x + v sin x.
По теореме о наложении решений ожидаемый вид частного решения имеет вид:
уч = уч1 + уч2 + уч3 = х ∙ (ax2 + bx + c) + е –х (dx + g) + u cos x + v sin x .
2.2. y′′ + 5y′ + 6y =3х2е х – хе –3х + 2х sin 2x.
2.3. y′′ + 2y′ + 2y =3х2е –х – хе –хsin x.
2.4. y′′ + 2y′ + y = х2sin x + 4 + 5х е –х .
3. Решить уравнение
3.1. у′′ – 2у′ + 5у = х е х cos2x + x2 – x + 2.
Р е ш е н и е. Общее решение соответствующего однородного уравнения у′′ – 2у′ + 5у = 0 имеет вид
(проверьте!)
уоо = (С1cos 2x + С2 sin 2x) е х .
В соответствие с теоремой о наложении решений данное дифференциальное уравнение представим в виде совокупности двух уравнений:
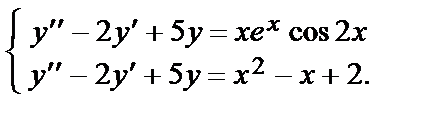
Частное решение первого уравнения ищем в виде
уч1 = x[(Ах + В) cos 2x + (Cх + D) sin 2x] е х ,
т.к. α ± β i = 1 ± 2i – корень характеристического уравнения k2 – 2k + 5 = 0, k = 1 ± 2i .
Соответствующие вычисления (проведите самостоятельно) дают уч1 = x ( 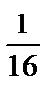 cos 2x +
cos 2x + 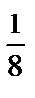 х sin 2x) е х.
х sin 2x) е х.
Частное решение второго уравнения ищем в виде уч2 = Аx2 + Вx + С, и, после нахождения А, В и С,
уч2 = 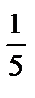 x2 –
x2 – 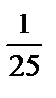 x +
x + 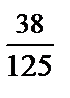 .
.
Общее решение исходного уравнения имеет вид
у = уоо + уч1 + уч2 = (С1cos 2x + С2 sin 2x) е х + x ( 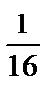 cos 2x +
cos 2x + 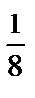 х sin 2x) е х +
х sin 2x) е х + 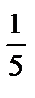 x2 –
x2 – 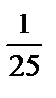 x +
x + 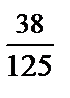 .
.
3.2. y′′ – 2y′ + y = х2 – х + 3 +2хcos x + sin x.
3.3. y′′ + 5y′ + 6y =(x – 2) е –3х + х2 + 2х – 3.
3.4. y′′ + 6y′ + 10y =(x + 6) cos 3x – (18x + 6) sin 3x + 2х е –3х cos x.
3.5. y′′ + 9y = е –3х (x – 2) + 14 + 63 х2.
3.6. y′′ – 2y′ + y = sin x + 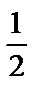 е х –
е х – 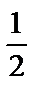 е –х.
е –х.
