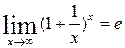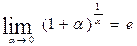Понятие числовой функции. Свойства функции

Пусть задано числовое множество Х. Правило, сопоставляющее каждому числу х из множества Х единственное действительное число у, называют

числовой функцией, заданной на множестве Х.

х- независимая переменная(аргумент);

у - зависимая переменная(функция).

Символическая запись функции имеет вид у = f(х)

Множество Х называется областью определения функции у и обозначается D(у). Е(у) - область (множество) значенийфункции у – множество всех значений переменной у, которые она принимает при всех допустимых значениях х.

Функция у = f(х)называется четной, если для любого значения х, взятого из области определения функции, значение -х также принадлежит области определения и выполняется равенство f(х) = f(-х).

Согласно определению, четная функция определена на мно­жестве, симметричном относительно начала координат. График четной функции симметричен относительно оси ординат (рис. 1).

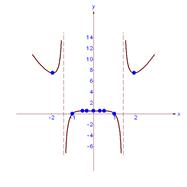
Рис. 1. График четной функции

Примеры четных функций: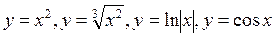

Функция у = f(х) называется нечетной, ес­ли для любого значения х, взятого из области определения функции, значение -х также принадлежит области опреде­ления и выполняется равенство f(x)= -f(x).

График нечетной функции симметричен относительно начала координат (рис. 2).

Примеры нечетных функций: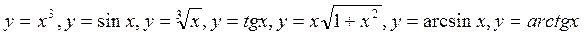

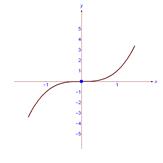
Рис. 2. График нечетной функции

При построении графиков четных и нечетных функций доста­точно построить только правую ветвь графика — для положи­тельных значений аргумента. Левая ветвь достраивается симметрично относительно оси оyдля четной функции и кососимметрично (т. е. симметрично относительно начала координат) для нечетной.

Конечно, большинство функций не являются ни четными, ни нечетными. Таковы, например, функции: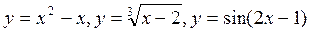

Функция у=f(х) называется периодической с периодом 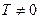,если при всех значениях х из области её определения выполняются равенства .

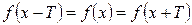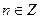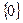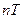Если Т – период функции, то при любом \ число также является периодом функции.

Наименьший положительный период функции называется её основным периодом.

Сумма, разность, произведение и частное двух функций, имеющих периодТ, обладает тем же периодом.

Сумма n периодических функций с периодами 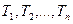имеет период 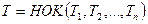. Если функция у = f(х) имеет период Т, то функция 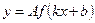имеет период .

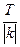Нулем функции называется такое действительное значение х, при котором значение функции равно нулю.

Для того чтобы найти нули функции, следует решить уравне­ние f(х)=0. Действительные корни этого уравнения являются нулями функции у=f(х),и обратно. Нули функции представляют собой абсциссы точек, в которых график этой функции либо пе­ресекает ось абсцисс, либо касается ее. Например, функция у = х³- 3x имеет нули в точках х = 0, 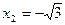, , 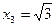а функция 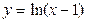имеет нуль в точке х = 2.

Функция может и не иметь нулей. Такова, например, функция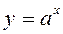

Область определения функции 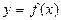совпадает с ОДЗ (областью допустимых значений) правой части 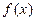, т.е. с множеством всех значений х, при которых 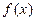вычисляется.

Задача . Найти область определения функции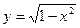

Решение. Первая часть вычисляется при всех значениях х, для которых подкоренное выражение неотрицательно. Поэтому область определения D(y) будет найдена из условия 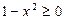. Решая это неравенство, получаем 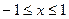, т.е.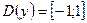

При анализе функции полезно проверить, обладает ли она свойством четности или нечетности. Наличие этих свойств позволяет упростить построение графика функции. Достаточно построить график функции для 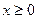. Тогда для четной функции часть графика для 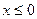получается симметричным отображением построенного графика относительно оси Оу, а для нечетной – относительно начала координат.

Задача . Выяснить, обладают ли данные функции свойством четности или нечетности:

а) 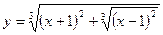б) .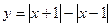

Решение.

а) .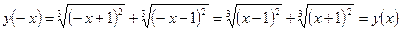

Итак, 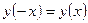и, следовательно, функция является четной.

б) 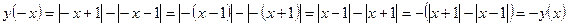, т.е. 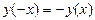и, следовательно, функция у(х) является нечетной. Здесь использовано свойство модуля (абсолютной величины) числа: .

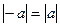Монотонность функции.

Переменную величину называют монотонной, если она изменяется только в одном направлении, т.е. либо только возрастает, либо только убывает. Очевидно, что движение точки х в сторону положительного направления оси абсцисс является мо­нотонно возрастающим, а в противоположную сторону - монотонно убывающим.

Функция у = f(х) называется монотонно возрастающей на интервале (а, b), если для любых х₁, и х₂, при­надлежащих этому интервалу, из неравенства х₂>х₁, следует неравенство f(х₂) >f(x₁) (рис. 3а).

Функция у = f(х) называется монотонно убывающей на интервале (а, b), если для любых х₁и х₂, принад­лежащих этому интервалу, из неравенства х₂>х₁, следует неравенство f(x₂) <f(x₁) (рис. 3б).

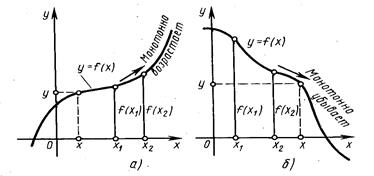
Рис. 3. Графики монотонно возрастающей и монотонно убывающей функций.

Естественно, что интервал (а, b)предполагается взятым из области определения функции.

Выпуклость функции

Говорят, что функция у = f(х) выпукла вверхв точке х₀, если существует окрестность точки х₀такая, что для всех ее точек х касательная к графику функции в точке М₀(х₀, у₀) лежит выше графика (рис. 4а). Говорят, что функция
у = f(х)выпукла внизв точке х₀, если существует окрестность точки х₀такая, что для всех ее точек х касательная к графику функции а точке М₀(х₀; у₀) лежит ниже графика (рис. 4б).

Если на некотором промежутке (а;b) все касательные к гра­фику функции
у = f(х) лежат выше (соответственно ниже) самого графика, то на данном промежутке функция выпукла вверх (со­ответственно выпукла вниз).

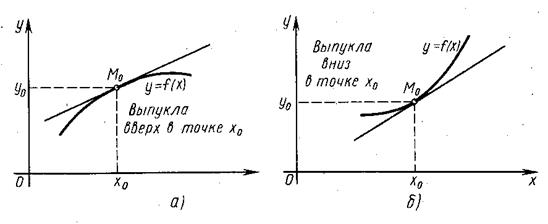
Рис. 4. Графики выпуклой функции

Вопросы для самопроверки:

1. Что называется функцией?

2. Какие способы задания функции Вы знаете?

3. Сформулируйте основные свойства функции.

Предел функции

Число А называется пределом функции в точке х₀ (или при х 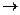х₀), если для любого положительного числа 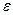найдется такое положительное число 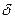( 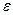), что для всех х 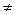х_0, удовлетворяющих неравенству 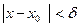, выполняется неравенство .

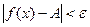Обозначают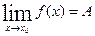

Функция 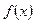называется бесконечно малой при 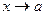, если .

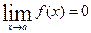Функция 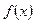называется бесконечно большой при 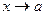, ес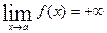ли или .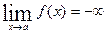

Теоремы о пределах

1.

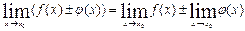
2.

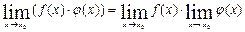
3.

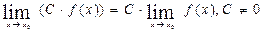
4.

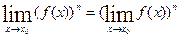
5.

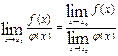
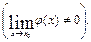
Первый замечательный предел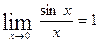

Второй замечательный предел