Связь круговой и линейной сверток

В общем случае круговая свертка не совпадает с линейной. Различия являются следствием предположения о периодическом продолжении сигналов за пределами окна анализа при вводе понятия ДПФ.

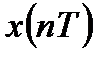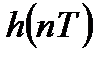Однако если имеются исходные конечные последовательности и с длительностями и , соответственно, то их можно дополнить нулями до числа отсчетов . Длины двух последовательностей становятся одинаковыми и равными длине линейной свертки исходных последовательностей. В этом случае линейная свертка исходных последовательностей будет соответствовать круговой свертке дополненных нулями исходных последовательностей и :

. (1.13)

В матричном виде можно записать соотношение для расчета линейной свертки сигналов для , через круговую свертку с длиной N=7:

. (1.14)

Быстрая линейная свертка

В случае, если необходимо обеспечить быстрое вычисление линейной свертки, в каждую из сворачиваемых последовательностей добавляют нулевые отсчеты в количестве, не меньшем длины результатов линейной свертки. Причем удобно выбрать количество нулей таким, чтобы длина получившейся последовательности была равна целочисленной степени двойки, чтобы можно было использовать алгоритм БПФ.

Таким образом, алгоритм фильтрации в частотной области записывается следующим образом:

1. Последовательность отсчетов входного сигнала и импульсная характеристика фильтра дополняются нулями так, чтобы длины последовательностей стали равными и не меньшими, чем сумма длин исходных последовательностей минус единица.

2. Вычисляются ДПФ дополненных нулями последовательностей.

3. Вычисленные ДПФ поэлементно умножаются.

4. Вычисляется обратное ДПФ от результата перемножения.

Метод быстрой линейной свертки предлагает преимущества меньшей вычислительной сложности по сравнению с прямым подходом, только если число значений, подлежащих свертке, достаточно велико.

Очевидно, что для получения линейной свертки двух N-точечных последовательностей и необходимо умножить каждое значение на каждое значение . Следовательно, N значений нужно перемножить с N значениями и потребуется всего умножений.

Рассмотрим теперь вычислительную сложность быстрой линейной свертки. Прибавление необходимых дополняющих нулей означает, что каждая преобразованная последовательность имеет длину точек. Предположим, что , где d – целое число. В этом случае число комплексных умножений для - точечного БПФ составит . Согласно уравнению быстрой линейной свертки необходимо вычислить два ДПФ и одно обратное ДПФ. Таким образом, необходимо вычислить три - точечных БПФ с операций комплексных умножений. Кроме этого, необходимо осуществить перемножение слагаемых результатов ДПФ входного сигнала и импульсной характеристики. Следовательно, общее количество операций комплексного перемножения составит . Так как дждое комплексное перемножение потребует четырех действительных умножений, необходимо выполнение действительных умножений.

Таким образом, непосредственное вычисление линейной свертки требует действительных умножений, в то время как метод быстрой свертки требует действительных умножений. Сравнительный анализ вычислительных затрат для быстрой линейной свертки и непосредственно линейной свертки приведен в Таблице 1.1. Из Таблицы видно, что быстрая свертка лучше прямого метода в том случае, если длина последовательностей превышает 128 дискретов данных. Для последовательности из 1024 точек быстрая свертка дает результат за время, в 10 раз меньшее, чем для линейной свертки.

Таблица 1.1. Вычислительные затраты линейной свертки и быстрой линейной свертки

N	Линейная свертка	Быстрая линейная свертка	Отношение затрат
		1 088	4.25
	1 024	2 560	2.5
	4 096	5 888	1.4375
	16 384	13 312	0.8125
	65 536	29 696	0.4531
	262 144	65 536	0,250
	1 048576	143 360	0,1367
	4 194 304	311 296	0.0742

Литература

Маркович И.И. Цифровая обработка сигналов в системах и устройствах: монография / И.И. Маркович; Южный федеральный университет. – Ростов н/Д: Издательство Южного федерального университета, 2012. – 236 с. (стр. 62)

Солонина А.И., Арбузов С.М. Цифровая обработка сигналов: Курс лекций. / А.И. Солонина, С.М. Арбузов. – СПб.: БХВ – Петербург, 2007 – 744 с (232 c.).