Описание линейной дискретной системы во временной области

3.1.2.1. Импульсная и переходная характеристики ЛДС

Во временной области линейная дискретная система (ЛДС) описывается импульсной характеристикой.

Импульсной характеристикой ЛДС называется ее реакция на единичный дискретный импульс при нулевых начальных условиях: рисунок 2.

Рисунок 2.1 – определение импульсной характеристики ЛДС

Единичный дискретный импульс описывается соотношением:

(2.1)

Импульсная характеристика является основной характеристикой линейной дискретной системы, так как с ее помощью легко определяется реакция на произвольное входное воздействие.

При описании ЛДС во временной области кроме импульсной характеристики используют переходную характеристику.

Переходной характеристикой ЛДС называют ее реакцию на единичный дискретный скачок при нулевых начальных условиях: рисунок 3.

Рисунок 2.2 – определение переходной характеристики ЛДС

Единичный дискретный скачок описывается соотношением:

(2.2)

3.1.2.2. Связь выходного сигнала ЛДС с входным во временной области

Во временной области соотношение вход-выход ЛДС описывается линейными уравнениями:

- формулой свертки при использовании импульсной характеристики;

- разностным уравнением, если используются параметры ЛДС.

Формула линейной свертки

Для получения уравнения свертки представим любой дискретный сигнал в виде линейной комбинации единичных дискретных импульсов :

.

Воспользовавшись свойствами аддитивности и определением импульсной характеристики линейной дискретной системы, можно получить уравнение свертки:

. (2.3)

В результате замены переменных можно получить второй вариант записи формулы свертки:

. (2.4)

Стандартное условное обозначение операции свертки имеет следующий вид:

.

Разностное уравнение

В общем случае ЛДС суммирует с некоторыми весовыми коэффициентами не только некоторое количество входных отсчетов, но и некоторое количество предшествующих выходных отсчетов:

, (2.5)

где - коэффициенты разностного уравнения.

Данная форма разностного уравнения иногда называется алгоритмом дискретной фильтрации. Если в левой части уравнения разместить только выходные отсчеты, а в правой части только входные, то получают форму записи, которую называют классическим разностным уравнением:

. (2.6)

Разностное уравнение является аналогом дифференциального уравнения аналоговой линейной системы для линейных дискретных систем.

. (2.7)

Переход дифференциального уравнения к дискретному аналогу в виде разностных уравнений может быть произведен путем замены производных конечными разностями:

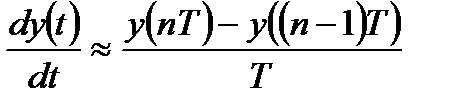; (2.8)

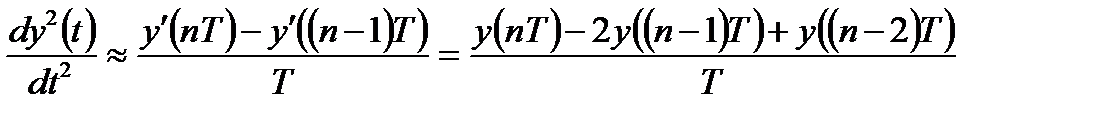. (2.9)

Вычисление выходного сигнала аналоговой системы может быть получено только приближенно путем замены операции интегрирования в интеграле Дюамеля одним из методов численного интегрирования. В то же время разностное уравнение или алгоритм дискретной фильтрации представляют собой алгоритм непосредственного вычисления выходного сигнала методом прямой подстановки при известном входном воздействии и предшествующих значениях выходного сигнала (реакции).