Оценка качества регулирования

Оценка качества по переходному процессу

Рассмотрим колебательный переходный процесс (рис. 4.29).

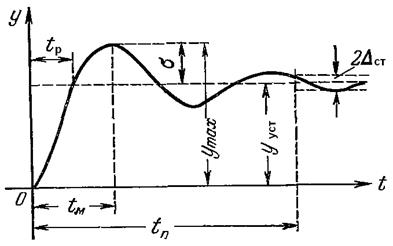
Рис. 4.29. Показатели качества переходного процесса

Показатели качества регулирования характеризуют быстродействие, запасы устойчивости и точность САР. К числу основных показателей относятся следующие.

Время переходного процесса (время регулирования) t_п – время от момента подачи воздействия на вход системы до момента практического затухания переходного процесса. Так как теоретически переходный процесс затухает в бесконечности, момент его практического затухания определяют, когда статическое отклонение Δ_ст не превышает 1…5 % от установившегося значения y_уст.

Перерегулирование σ – максимальное отклонение выходной величины от установившегося значения. Измеряется в процентах от установившегося значения:

.

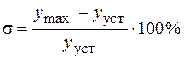Перерегулирование связано с запасами устойчивости системы. Для систем с колебательным характером переходного процесса считается нормальным перерегулирование в пределах 10…30 %, что соответствует запасам устойчивости по амплитуде L_у = 6…20 дБ и по фазе j_у = 30…60 %.

Дополнительно рассматривают время разгона t_р – время от момента подачи воздействия на вход системы до момента первого достижения установившегося значения. Максимальное значение этого параметра ограничивается заданным быстродействием, минимальное – заданными перегрузками. Для процессов без перерегулирования вместо времени разгона оценивают время до момента достижения половины установившегося значения.

Для построения переходного процесса требуется решение дифференциального уравнения системы, поэтому на практике для оценки качества часто используют различные критерии, некоторые из которых рассмотрены ниже.

Частотные критерии качества

Позволяют оценить качественные показатели системы по ее частотным характеристикам.

Ранее при рассмотрении критерия устойчивости Найквиста была рассмотрена методика определения запасов устойчивости по АФЧХ или ЛАЧХ и ЛФЧХ разомкнутой системы.

По АЧХ замкнутой системы можно косвенно оценить запасы устойчивости и приблизительно время переходного процесса (рис. 4.30).

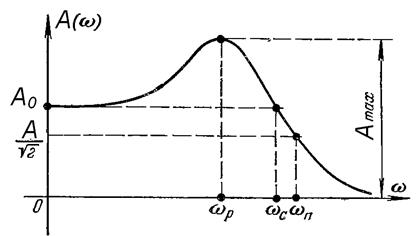
Рис. 4.30. АЧХ замкнутой системы

Для оценки запасов устойчивости используется показатель колебательности М:

.

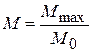Ранее указанным нормативным значениям перерегулирования и запасов устойчивости соответствуют значения М = 1,1…1,5.

Резонансная частота w_р близка к частоте колебаний в переходном процессе.

Время переходного процесса приближенно определяется по частоте среза w_с или верхней границе полосы пропускания w_п:

.

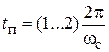Наибольшую информацию о качестве можно получить по ВЧХ замкнутой системы.

1. По виду ВЧХ можно сделать вывод о характере переходного процесса (рис. 4.31).

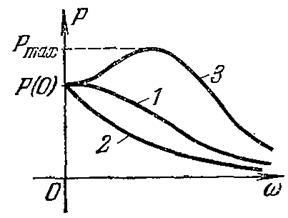
Рис. 4.31 – Виды ВЧХ

Виду 1 соответствует колебательный переходный процесс с σ < 18 %, виду 2 – монотонный, виду 3 – колебательный с σ > 18 %.

2. Значение Р(0) соответствует установившемуся значению переходного процесса.

3. Для ВЧХ типа 3 .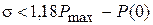

4. Приближенная оценка времени регулирования 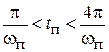, где w_п – интервал положительных значений ВЧХ (рис. 4.32).

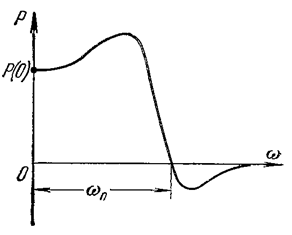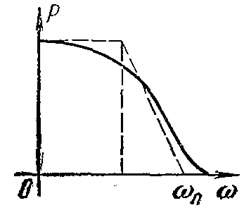Рис. 4.32 – Частота w_п на ВЧХ

5. Интегрированием ВЧХ можно получить кривую переходного процесса:

.

Корневые критерии качества

О качестве системы можно судить по расположению корней характеристического уравнения на комплексной плоскости. Для системы 3-го порядка можно рассмотреть 3 вида расположения корней (рис. 4.33).

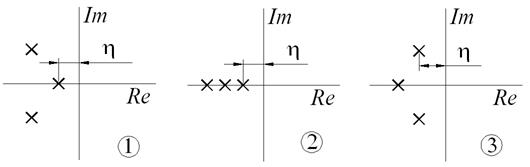
Рис. 4.33. Расположение корней на комплексной плоскости

Варианты расположения корней 1 и 2 соответствуют апериодическим переходным процессам (к мнимой оси ближе действительный корень). Вариант 3 – колебательным (к мнимой оси ближе пара комплексных корней). По расстоянию от мнимой оси до ближайшего корня можно судить о быстроте затухания переходного процесса. Для апериодического процесса

,

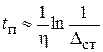для колебательного

.

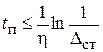Если принять статическую ошибку в пределах 5 %, т. е. Δ_ст = 0,05

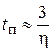или .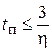

Для колебательных переходных процессов по координатам корней на комплексной плоскости оценивают колебательность (не путать с показателем колебательности М)

.

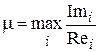По значению колебательности можно рассчитать перерегулирование:

.

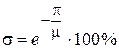На оценке расположения корней основан метод Вышнеградского. Для его использования характеристическое уравнение системы a₀р³ + a₁р² + a₂р + a₃ = 0 приводят к нормированному виду:

q³ + Aq² + Bq + 1 = 0,

, , /

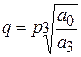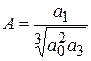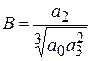Для оценки качества системы рассчитывают параметры Вышнеградского А и В и наносят точку с получившимися координатами на специальную диаграмму Вышнеградского (рис. 4.34).

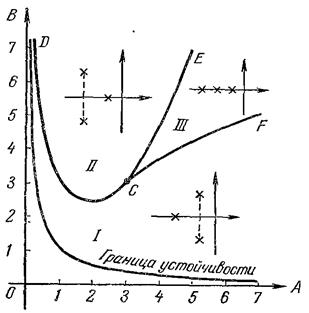
Рис. 4.34. Диаграмма Вышнеградского

В зависимости от того, в какой зоне находится отметка, можно судить о поведении системы. Зона ниже границы устойчивости (ее уравнение АВ = 1) соответствует неустойчивым системам. Для зоны I переходный процесс будет колебательным, для зон II и III – апериодическим (рис. 4.35).

Рис. 4.35. Переходные процессы в соответствии с диаграммой Вышнеградского

Для получения дополнительных сведений о системе на диаграмму Вышнеградского накладываются изолинии, позволяющие определить, например, показатель колебательности или быстродействие системы.