Силы давления жидкости на плоские и криволинейные поверхности.

Гидродинамика.

· Основные параметры потока в живом сечении

Расход потока Q - объем жидкости V, протекающей за единицу времени t через живое сечение ω.

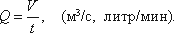
Средняя скорость потока υ - скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

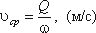
Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное - течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.).

· Виды расхода и способы его измерения, расходометры

Различают объёмный, массовый и весовой расходы жидкости.

Объёмный расход жидкости это объём жидкости, протекающей в единицу времени через живое сечение потока. Объёмный расход жидкости измеряется обычно в м3/с, л/с. Он вычисляется по формуле

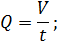
где Q - объёмный расход жидкости,

V - объём жидкости, протекающий через живое сечение потока,

t – время течения жидкости.

Массовый расход жидкости это масса жидкости, протекающей в единицу времени через живое сечение потока. Массовый расход измеряется обычно в кг/с, г/с или т/с и определяется по формуле

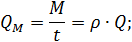
где QM - массовый расход жидкости,

M -масса жидкости, протекающий через живое сечение потока,

t – время течения жидкости.

Весовой расход жидкости это вес жидкости, протекающей в единицу времени через живое сечение потока. Весовой расход измеряется обычно в Н/с, кН/с. Формула для его определения выглядит так:

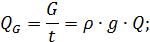
где QG - весовой расход жидкости,

G - вес жидкости, протекающий через живое сечение потока,

t – время течения жидкости.

Расход элементарной струйки – объем жидкости dV, проходящей через живое сечение струйки в единицу времени. Таким образом:

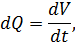
Если последнее выражение проинтегрировать по площади живого сечения потока можно получить формулу объёмного расхода жидкости, как сумму расходов элементарных струек

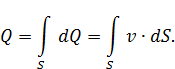
Применение этой формулы в расчетах затруднительно, так как расходы элементарных струек жидкости в разлчных точках живого сечения потока различны. Поэтому чаще используют среднюю скорость потока .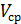

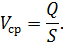
Уравнения объемного расхода во всех сечениях элементарной струйки

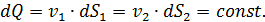
Аналогичные уравнения можно составить и для потока конечных размеров

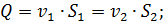
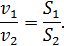
Это уравнения неразрывности потока капельной жидкости.

Расходоме́р — прибор, измеряющий объемный расход или массовый расход вещества, то есть количество вещества (объем, масса), проходящее через данное сечение потока, например, сечение трубопровода в единицу времени. Если прибор имеет интегрирующее устройство (счетчик) и служит для одновременного измерения и количества вещества, то его называют счетчиком-расходомером.

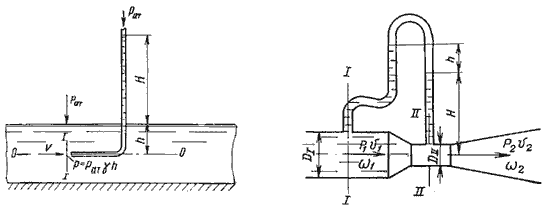
Рис. 3.7. Трубка Пито и pасходомерВентури

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:

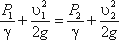
или

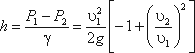
Используя уравнение неразрывности

Q = υ₁ω₁ = υ₂ω₂

сделаем замену в получено выражении:

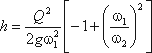
Решая относительно Q, получим

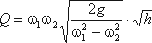
Выражение, стоящее перед 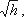, является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

· Основные уравнения гидродинамики :

Уравнение неразрывности потока отражает закон сохранения массы: количество втекающей жидкости равно количеству вытекающей

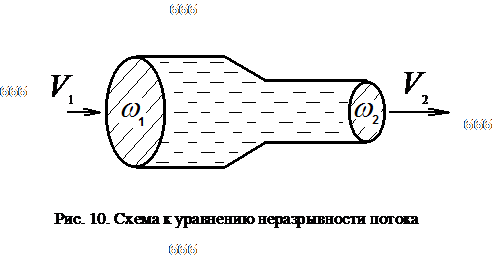
Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q₁=Q₂= const, откуда

ω₁υ₁ = ω₂υ₂

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

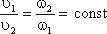
Уравнение Бернулли

Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).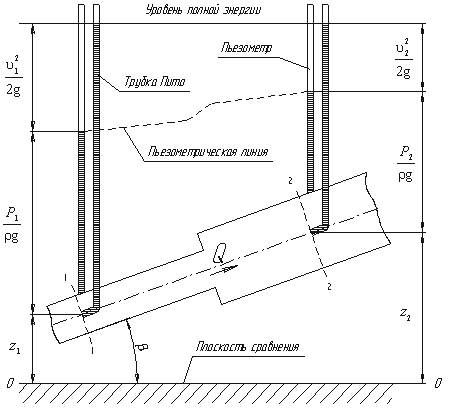

Рис.3.5. Схема к выводу уравнения Бернулли для идеальной жидкости

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.

Для измерения давления жидкости применяют пьезометры - тонкостенные стеклянные трубки, в которых жидкость поднимается на высоту 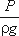. В каждом сечении установлены пьезометры, в которых уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

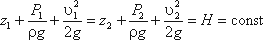
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

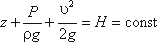
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

z1 и z2 - удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;
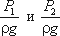- удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;
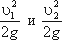- удельные кинетические энергии в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

Уравнение количества движения

Для материального тела массой 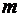, движущегося со скоростью 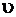, изменение количества движения за время 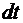вследствие действия силы 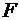выразится векторным уравнением

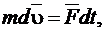(1.4.12)

где 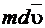- приращение количества движения, обусловленное импульсом .

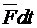Применим эту теорему механики к участку потока жидкости с расходом 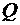между сечениями 1-1 и 2-2 в условиях установившегося течения (рис. 1.4.3).

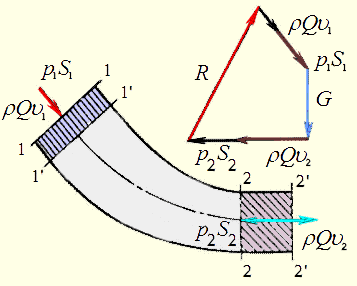Рис. 1.4.3. Применение уравнения количества движения к жидкости

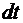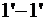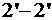За время этот участок потока переместится в положение, определяемое сечениями и , а приращение количества движения будет равно 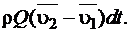Это приращение количества движения обусловлено импульсом всех внешних сил, действующих на объем жидкости между сечениями 1-1 и 2-2, а именно: сил давления 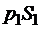и 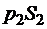в первом и втором сечениях, силы тяжести 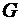всего объема, а также реакции 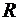стенок трубы, которая складывается из сил давления и трения, распределенных по боковой поверхности объема. Если обозначить вектор равнодействующей всех сил через 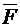, то 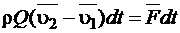, или после сокращения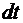

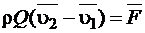. (1.4.13)

Согласно уравнению (1.4.13) теорема Эйлера об изменении количества движения объема жидкости может быть сформулирована следующим образом: при установившемся движении вектор равнодействующей всех внешних сил, действующих на жидкость в фиксированном объеме, равен геометрической разности количества движения жидкости, вытекающей из этого объема и втекающей в него за единицу времени.

Уравнение (1.4.13) можно записать в виде

,

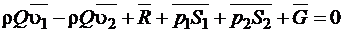в соответствии с этим построить замкнутый многоугольник векторов (рис. 1.4.3) и определить искомую силу 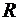реакции стенок трубы. В связи с тем, что в последнем уравнении вектор 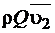имеет знак “минус”, при построении многоугольника векторов он направлен в сторону, обратную действительному его направлению.

· Местные потери напора(давления) и потери по длине

Местные потери напора вызываются сопротивлениями в арматуре, фасонных частях и оборудовании, вследствие сужения и расширения потока, изменения направления движения жидкости, слияния и разделения потока и т. п.

Местные потери напора определяют как произведение скоростного напора непосредственно вблизи местного сопротивления 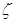,по формуле

.

U – скорость движения, м/c
p – плотность, кг/м³

Потери по длине

При ламинарном режиме движения существуют лишь продольные составляющие скоростей. В этом случае силы сопротивления движению возникают вследствие трения между слоями жидкости, т. е. зависят от вязкости жидкости и не зависят (почти) от состояния стенок

При турбулентном режиме закон распределения скоростей по живому сечению более сложен; в большей части сечения скорости близки к средней и резко падают в тонком слое у стенок, доходя до нуля

Потери напора на трение по длине потока, возникающие при равномерном напорном движении жидкости в трубах, определяют по уравнению

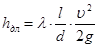
где l – длина участка трубы, м; d –внутренний диаметр трубопровода, м; v – средняя скорость потока, м/сек; g –ускорение свободного падения, м/сек2; 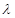– безразмерный коэффициент гидравлического трения.