Понятие вектора. Сложение векторов

Определение 1. Отношение эквиполлентности направленных отрезков пространства разбивает все направленные отрезки пространства на классы, каждый из которых мы называем вектором в пространстве.

Векторы будем обозначать стрелкой сверху: 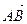, . Вектор, заданный нулевым направленным отрезком называем нуль-вектором .

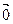Эквиполлентные направленные отрезки, составляющие вектор называются представителями вектора. Равенство векторов предполагает совпадение соответствующих классов эквиполлентных направленных отрезков.

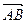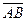
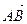
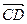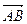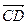Длиной вектора называется длина его представителя и обозначается: | |, | |. Далее вводим понятия сонаправленности векторов, в заисимости от их представителей: ­­ Û ­­ , ­¯ Û ­¯ .

Теорема 1. Если 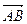= 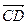, то = .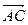

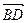Доказательство. Так как 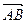= 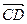, то ~ . В силу теоремы 3 § 1 середины отрезков АD и CB совпадают. Обозначим эту точку О. Но и для направленных отрезков 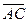и 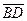точка О является точкой пересечения отрезков АD и CB. Так как она является их серединой, то в силу теоремы 3 § 1 получим 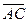~ 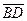, а, следовательно, = .

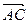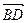Теорема доказана.

В дальнейшем мы будем часто сталкиваться с понятием откладывания вектора от данной точки. Рассмотрим это понятие.

Пусть - произвольный вектор, а С– некоторая точка пространства. Рассмотрим произвольный представитель вектора . Наша задача построить такую точку D, для которой ~ . Согласно теореме 1 находим середину отрезка CB и, обозначив ее О, находим точку D при условии, что О является серединой отрезка АD. В силу признака эквиполлентности двух направленных отрезков (теорема 3 § 1) получим ~ . Поэтому = .

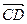Построение направленного отрезка называют откладыванием вектора от данной точки С.

Самостоятельно доказать, что построенная точка D единственная.

Определение 2. Векторы и называются коллинеарными, если существует прямая, которой они параллельны.

Обозначаем: || .

Следует отметить, что коллинеарные векторы имеют либо одно и то же направление, либо противоположные.

Определение 3. Вектор называют параллельным плоскости, если на плоскости существует прямая, которой данный вектор параллелен.

Сложение векторов

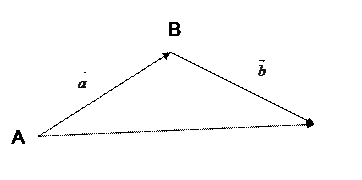
На множестве векторов определяется операция сложение векторов следующим образом. Пусть заданы векторы и . Выберем произвольно точку А и от точки А откладываем вектор . Получим точку В : 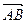= . Далее, от точки В откладываем вектор . Получим точку С: 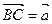. Точки А и С определяют направленный отрезок 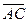, который в свою очередь определяет вектор 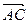= 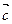. Вектор 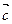называем суммой векторов и . Обозначаем: + = .

C

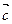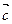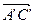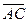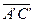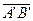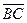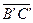В нашем определении была произвольно выбрана точка А. Поэтому необходимо показать, что от выбора точки А вектор не зависит. Пусть А¢ другая точка. Сделаем те же построения и получим вектор . Покажем, что ~ . Действительно, из построения имеем, что ~ и ~ . Согласно теореме 1 имеем: 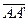~ 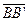и 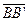~ 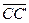. В силу транзитивности отношения эквиполлентности направленных отрезков получим 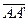~ 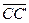. Отсюда, согласно теореме 1 имеем: 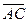~ 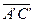, а это говорит о том 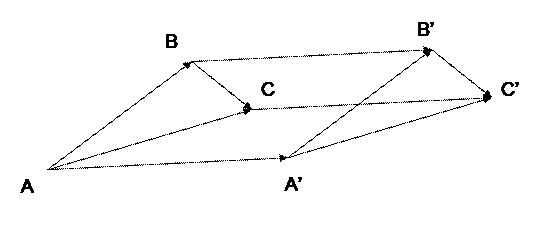, что от выбора точки А вектор 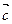не зависит.

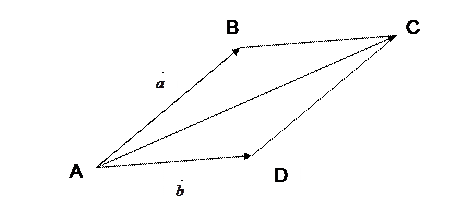
Указанное здесь правило сложения векторов называют правилом треугольника.

Если векторы и не коллинеарные, то откладывая от точки А оба вектора и , мы получим их сумму как вектор определенный направленным отрезком 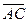, где точка С - вершина параллелограмма, построенного на представителях векторов и , отложенных от точки А и противоположная точке А. Действительно, если применить правило треугольника, то получим

+ = + = .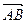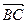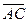